Course Introduction
Slides version: intro_slides.html Website version: intro.html
課程說明 (Course Description)
本課程之內容包括:物件導向程式設計 (OOP)、C/C++ OOP 寫法、程式寫作技巧與觀念及實作範例。透過課堂解釋實作範例搭配作業練習各主題的語法或技巧。
The course will introduce the Object-Oriented Programming (OOP), the writing of OOP in C/C++ and the concepts and skills of programming. Each theme will be instructed with examples and hands-on labs in-class or off-class.
指定用書 (Text Books)
- 課程講義,公布於課程網站上。 (Lecture notes, published on the course website.)
參考書籍 (References)
-
Paul Deitel, and Harvey Deitel, C++ How to Program, 10/e (主要參考, Primary reference)
-
Stephen Schach, Object-Oriented and Classical Software Engineering, 8/e
-
Introduction to C++ | Electrical Engineering and Computer Science | MIT OpenCourseWare
-
Introduction to C and C++ | Electrical Engineering and Computer Science | MIT OpenCourseWare
教學方式 (Teaching Method)
透過講義解說各主題的實作技巧,由學生練習、測試與完成相關之課堂實作或作業。 課堂會採用實體及線上混合教學,學生可在滿足防疫規定下參加現場授課,同時於線上平台直播,同學也可同步於線上平台留言發問。 學生課後可透過 eeclass 討論區及預約時段與授課老師及助教討論。
The course will introduce each theme with lecture notes. Students will practice each theme with Homeworks and hands-on labs in-class or off-class. The course will hold both physically and online. Students can attend class physically under Taiwan CDC COVID-19 guideline. Also, the course will stream on online streaming platform(s). Students can discuss in real-time on the online streaming platform(s). After class, students can use the discussion forum in the NTHU eeclass or make a reservation with instructor or TA.
教學進度 (Syllabus) (Project Version)
(5/15 updated) 週次皆為暫定安排,會依實際授課情形調整。
| 課程 (Lecture) | 主題 (Theme) |
|---|---|
| Lecture 1 (2/17) | Course Introduction |
| Sturcture and Class | |
| Lab 1 (2/17) | Programming Environment & Class Helloworld |
| Lecture 2 (2/24) | Class Design 101 |
| Lecture 3 (3/3) | Class Members & Methods |
| Lecture 4 (3/10) | Class Constructor & Modifer |
| Lab 4 (3/10) | Complex Number |
| Lecture 5 (3/24) | Collaborate with Other Classes |
| Lecture 6 (3/31) | Operator & Operator Overloading |
| Lab 6 (3/31) | Complex Number Calculator |
| Lecture 7 (4/7) | Introduction to Object Oriented Programming & Design |
| Lecture 8 (4/14) | OOP: Inheritance (1) |
| Project 8 (4/14) | Midterm Project Announcement |
| Demo 9 (4/21) | Midterm Project Demo |
| Lecture 10 (4/28) | OOP: Inheritance (2) |
| Lecture 11 (5/5) | OOP: Polymorphism (1) |
| Lecture 12 (5/12) | OOP: Polymorphism (2) |
| Lab 12 (5/12) | Complex Number's Geometry & Operations |
| Lecture 13 (5/19) | File Processing (1) |
| Lecture 14 (5/26) | File Processing (2) |
| Lab 14 (5/26) | File Export of Complex Number's Geometry |
| Lecture 15 (6/2) | Advanced I/O & Exception Handling |
| Project 16 (6/9) | Final Project Announcment |
| Lecture 16 (6/9) | (Extra) C++ Image Export & Matplot++ |
| Demo 17 (6/16) | Final Project Demo |
| Lecture 18 (online) | (Extra) Google Test for Class |
成績考核 (Evaluation)
(4/7 updated) 暫定,會依實際授課情形調整。 (Tentative, will change during the course)
學期成績 (Grade) = 作業/實作 (Homework/Lab), 50% + 期中 Project (Midterm Project), 25% + 期末 Project (Midterm Project), 25% + Bonus, 15%
相關網頁(Personal Website)
課程網頁 (Course website): https://stevenokm.github.io/i2p-nthu-math/i2p2

課程資訊
課程上課時間
- 每週四 15:30 - 18:10
- 前 1 - 1.5 小時講解今日主題
- 之後時間開放同學於現場或線上即時提問
課程上課地點(實體教室)

課程上課地點(網路)
- Youtube (Link: 110 程式設計二 上課錄影 - YouTube)
- Teams (Link: 110 程式設計二)
- 申請方式: Office 365 服務 (nthu.edu.tw)
- 外校同學可提供 office 365 帳號給助教協助加入團隊。

加簽規則
- 本課程開放加簽,原則上限制人數為 47 人,且參加實體課程需配合防疫規定。
- 請使用電子加簽系統加簽。
- 目前選課系統上限為本系大一生 37 人,並另有 10 人須審核加簽名額。
- 外系同學可線上加簽系統加選課程。
作業
- 作業會公布在課程網頁上,並使用 eeclass 平台繳交作業。
- eeclass 連結: https://eeclass.nthu.edu.tw/course/8073
- 同學可多加利用 eeclass 的討論區進行討論。
- 作業會使用自動化工具檢查,若有批改上有問題可與助教詢問。
- 作業抄襲一律 0 分計算,並且不計入繳交次數。
- 作業須準時繳交,遲交則得到原始成績 80% 的分數。

期中 / 期末 Project + Demo
- 題型: 1-2 題基本題 + 1-2 題進階題 (與上學期期中/期末評量題型相同)
- 繳交期限: 公布後次週三 23:59:59
- 可遲交,遲交則得到原始成績 80% 的分數
- 未 Demo 則該次 Project 成績為 0 分
- Demo 時間: 公布後次週四 15:30 - 18:30 (與上學期期中/期末評量時間相同)
- Demo 時間表 (連結待補)
- 每位同學 10 分鐘 Demo 時間,請務必準時參加
- 遲交的同學仍須另外約 Demo 時間,最晚不得超過該次 Demo 時間後的次週四 18:30
- e.g. 該 Project 4/14 公布後,同學遲交的話,需於 4/25 18:30 前約 Demo
- Demo 地點: 綜三館 315 電腦教室
- 若改為遠距教學時,則使用 Teams 進行 Demo
- Demo 流程:
- 從 eeclass 上下載最新版本的 Project 程式碼
- 使用 windows + mingw 環境下的 g++ 編譯程式碼
- 簡述如何實作
- 助教會隨機挑選一個擬定好的問題,請同學試著解出問題 (白板題)
- 部分程式碼/member function的運作邏輯?
- 部分程式碼/member function的用途?
- 輸入至輸出的程式碼運作流程?
- 調整部分程式碼/member function後,部分程式碼的運作流程/結果會如何改變?
- 範例題目會於 Demo 前公布於課程網站,供同學參考題型,實際題目以 Demo 為主。
- 公布時間不晚於 Demo 前一日 18:00,並會於 eeclass 上公布。
老師資訊
洪奕文 E-mail: s106062802@m106.nthu.edu.tw
Office Hours: Every Mon. 14:00 - 15:00
Office Room: R2341, 2F, EECS Building
Note: 若要來研究室詢問問題,請 一定要預約時間 ,臨時來研究室詢問 不保證 能夠當下開放詢問。 若要約 teams 詢問也可以約 Office Hour 時段詢問。
TA infos
許廷碩 E-mail: tim890727@gmail.com
TA Hours: 寫信詢問
Bonus
- 課程內容如果有錯誤,可以在每頁的右上方 "Suggest an edit" 使用 Github 進行修改,修改完畢後利用 Pull Request 的方式提交。
- 提交時註明學號以及姓名,並且每提交一次可以增加學期分數,配分依據修改幅度而訂。
- Github Commit 提交教學請參考 Lecture 15: Github Tutorial - Introduction to Programming (I)
- 於 eeclass 討論區參與討論,每提交一次可以增加學期分數,配分依據提交次數而訂。
- 每人總增加分數不超過 15 分
Visual Studio Code Tutorial (315 classroom)
使用 VSCode 環境
點擊兩下,打開桌面上的 Visual Studio Code。

在文字輸入區輸入以下程式碼
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main()
{
vector<string> msg {"Hello", "C++", "World", "from", "VS Code", "and the C++ extension!"};
for (const string& word : msg)
{
cout << word << " ";
}
cout << endl;
}

編譯 & 執行 Hello world!
In VSCode: Terminal -> New Terminal

In VSCode Terminal:
$ g++ test.cpp
$ ./a.out
Hello C++ World from VS Code and the C++ extension!
$
測試編譯以及除錯
測試編譯
- 點擊左方test.cpp檔案後,在要中斷的程式碼行號左邊點一下,會出現紅點,如下圖示範:

- 按下
ctrl+shift+B按鍵,或上方terminal -> Run Build Task,如下圖示範:
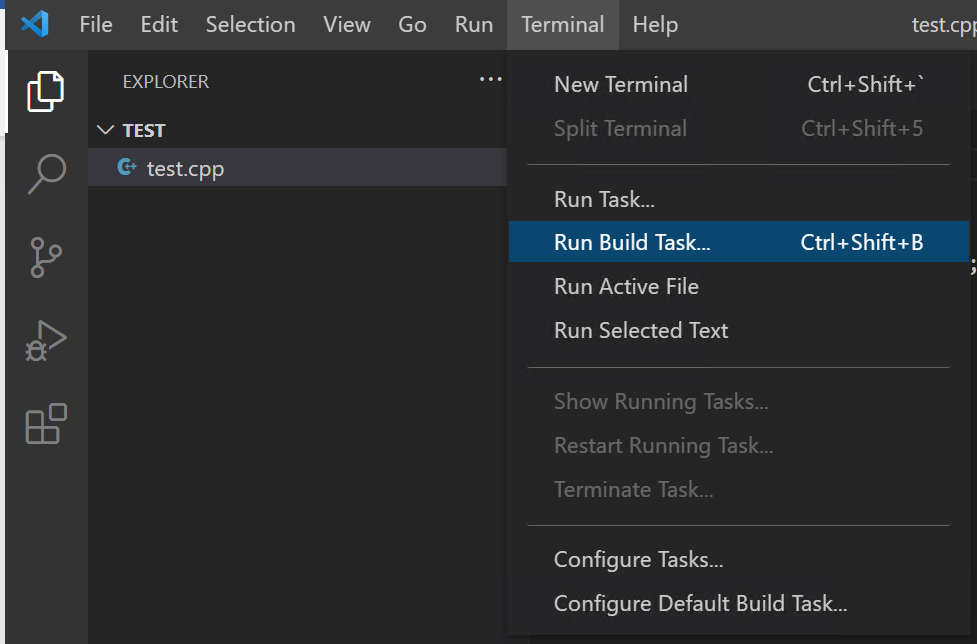
- 此時上方會出現以下畫面,選擇中間選項使用 g++ 編譯檔案,如下圖示範:
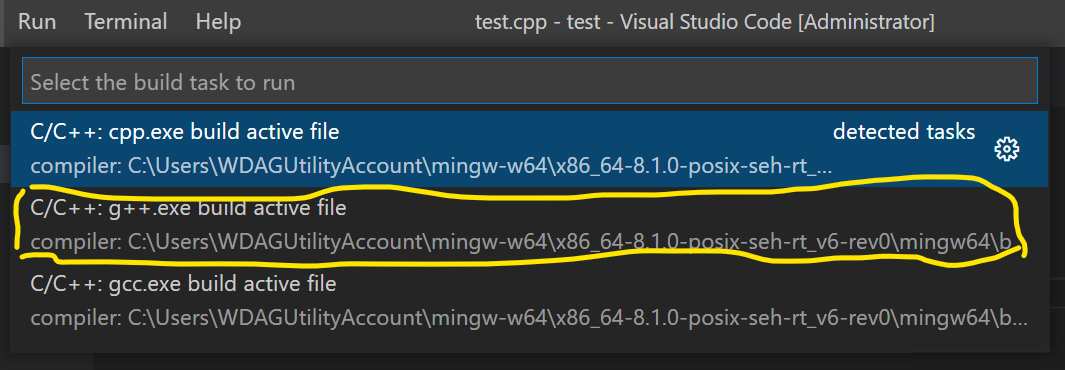
- 設置正確的話,此時下方會出現編譯成功完成的提示,如下圖示範:

測試除錯
-
完成前項
測試編譯的所有流程 -
按下左方三角形按鈕後選擇
Run and Debug,如下圖示範:

- 此時上方會依序出現相關提示,選擇預設的即可,如下圖示範:


- 若設定正確的話,會看到程式停留在選取的那一行,如下圖示範:
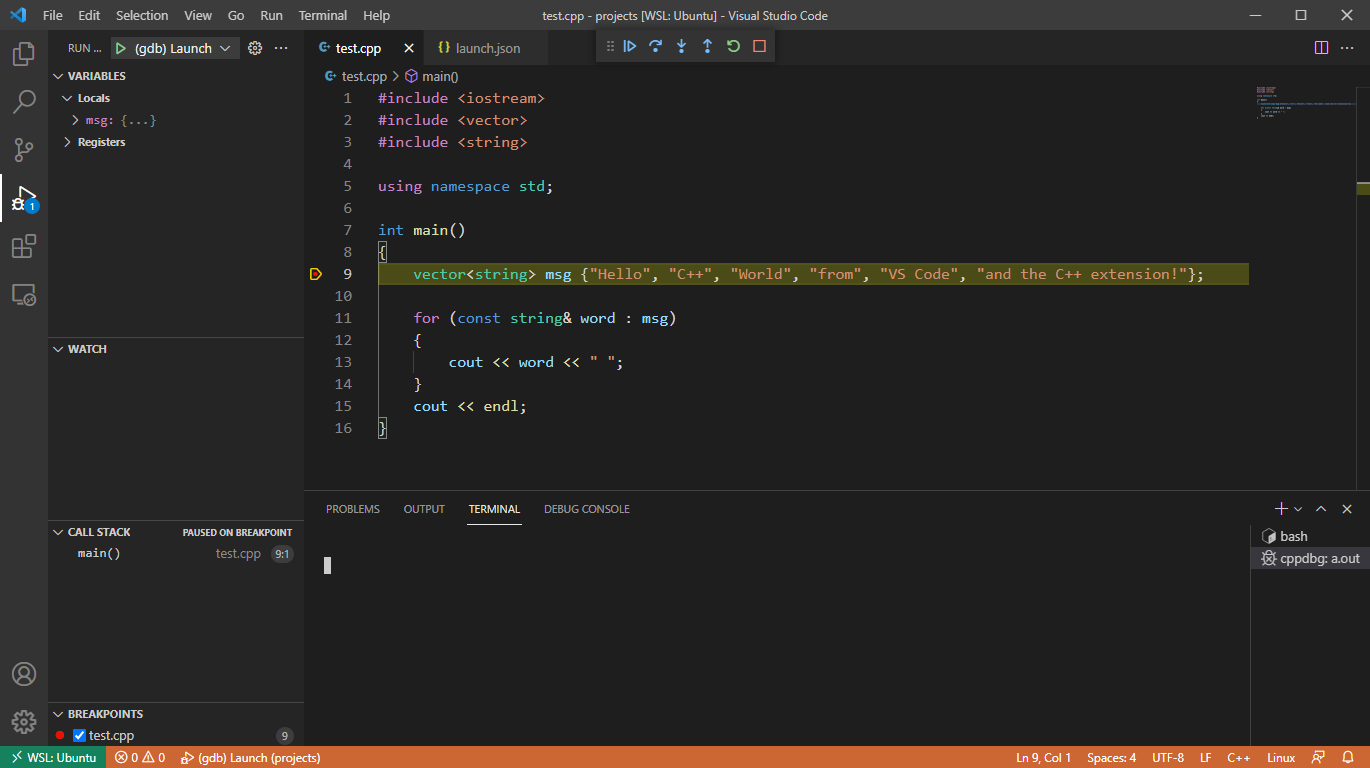
Visual Studio Code Tutorial
設定 VSCode 環境 (Linux)
安裝 GCC
打開 終端機 輸入以下指令:
sudo apt update
sudo apt install -y build-essential g++ gdb
g++ -v
Wrong:
Correct:
安裝 VSCode & C++ plugin
Install VSCode: https://code.visualstudio.com/docs/setup/linux
Install the C++ extension for VSCode: https://marketplace.visualstudio.com/items?itemName=ms-vscode.cpptools
新增專案 (Hello world!)
在 終端機 輸入以下指令:
$ mkdir projects
$ cd projects
$ code .
In VSCode: Exploer -> New File
輸入 test.cpp
在文字輸入區輸入以下程式碼
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main(void)
{
vector<string> msg {"Hello", "C++", "World", "from", "VS Code", "and the C++ extension!"};
for (const string& word : msg)
{
cout << word << " ";
}
cout << endl;
return 0;
}

編譯 & 執行 Hello world!
In VSCode: Terminal -> New Terminal

In VSCode Terminal:
$ g++ test.cpp
$ ./a.out
Hello C++ World from VS Code and the C++ extension!
$
Debugger
可以設置中斷點,方便程式除錯。
launch.json
In VSCode: Exploer -> New Folder
輸入 .vscode
In VSCode: Exploer -> New File
輸入 launch.json
在文字輸入區輸入以下設定檔
{
"version": "0.2.0",
"configurations": [
{
"name": "(gdb) Launch",
"type": "cppdbg",
"request": "launch",
"program": "${workspaceFolder}/a.out",
"args": [],
"stopAtEntry": false,
"cwd": "${workspaceFolder}",
"environment": [],
"externalConsole": false,
"MIMode": "gdb",
"setupCommands": [
{
"description": "Enable pretty-printing for gdb",
"text": "-enable-pretty-printing",
"ignoreFailures": true
}
]
}
]
}
編譯 & 執行 Debugger
In VSCode Terminal:
$ g++ -g test.cpp
$
插入中斷點
在要中斷的程式碼行號左邊點一下

In VSCode: Run -> Start Debugging F5


NOTE: 安裝完後可以在 File -> Oper Recent 開啟 WSL 的工作區 (後綴有 WSL:Ubuntu)
設定 VSCode 環境 (macOS)
安裝 g++
打開 終端機 輸入以下指令:
xcode-select --install
g++ -v
Wrong:

Correct:

安裝 VSCode & C++ plugin
Install VSCode: https://code.visualstudio.com/docs/setup/mac
Install the C++ extension for VSCode: https://marketplace.visualstudio.com/items?itemName=ms-vscode.cpptools
Note: 要加入 code 到環境變數 PATH 內。
- 打開 Command Palette (⌘ Shift P) 後輸入
shell command,就可以找到 Shell Command: Install 'code' command in PATH

- 重新啟動 終端機
新增專案 (Hello world!)
在 終端機 輸入以下指令:
$ mkdir projects
$ cd projects
$ code .
In VSCode: Exploer -> New File
輸入 test.cpp

在文字輸入區輸入以下程式碼
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main(void)
{
vector<string> msg {"Hello", "C++", "World", "from", "VS Code", "and the C++ extension!"};
for (const string& word : msg)
{
cout << word << " ";
}
cout << endl;
return 0;
}

settings.json
In VSCode: Exploer -> New Folder
輸入 .vscode

In VSCode: Exploer -> New File
輸入 settings.json
在文字輸入區輸入以下設定檔
{
"C_Cpp.default.cppStandard": "c++17"
}
編譯 & 執行 Hello world!
In VSCode: Terminal -> New Terminal

In VSCode Terminal:
$ g++ -std=c++17 -stdlib=libc++ test.cpp
$ ./a.out
Hello C++ World from VS Code and the C++ extension!
$
Debugger
可以設置中斷點,方便程式除錯。
安裝 CodeLLDB plugin
Install the CodeLLDB extension for VSCode: https://marketplace.visualstudio.com/items?itemName=vadimcn.vscode-lldb
launch.json
In VSCode:
選擇 .vscode
In VSCode: Exploer -> New File
輸入 launch.json
在文字輸入區輸入以下設定檔
{
"version": "0.2.0",
"configurations": [
{
"name": "(gdb) Launch",
"type": "lldb",
"request": "launch",
"program": "${workspaceFolder}/a.out",
"args": ["-arg1", "-arg2"],
"stopAtEntry": false,
"cwd": "${workspaceFolder}",
"environment": [],
"externalConsole": false,
"MIMode": "lldb",
"setupCommands": [
{
"description": "Enable pretty-printing for gdb",
"text": "-enable-pretty-printing",
"ignoreFailures": true
}
]
}
]
}
編譯 & 執行 Debugger
In VSCode Terminal:
$ g++ -std=c++17 -stdlib=libc++ -g test.cpp
$
插入中斷點
在要中斷的程式碼行號左邊點一下

In VSCode: Run -> Start Debugging F5

使用 VSCode server
使用 web IDE
Notice: 僅提供方便使用的網站,與 VSCode 環境不同,需自己學習使用。
- https://replit.com/
- 需註冊帳號,有部分功能需付費。
- https://www.onlinegdb.com/
- 無須註冊帳號,僅有基本功能。
- https://www.online-ide.com/
- 無須註冊帳號,僅有基本功能。
Reference:
Visual Studio Code Tutorial (WSL/windows + mingw)
設定 VSCode 環境 (WSL)
NOTE: 安裝教學影片 WSL Tutorial
安裝 WSL & GCC
Install WSL: https://docs.microsoft.com/en-us/windows/wsl/install
啟動 WSL Ubuntu
在 WSL Ubuntu 輸入以下指令:
sudo apt update
sudo apt install -y build-essential g++ gdb
g++ -v
Wrong:

Correct:

安裝 VSCode & Remote - WSL plugin
Install VSCode: https://code.visualstudio.com/docs/setup/windows
Install the Remote - WSL extension for VSCode: https://marketplace.visualstudio.com/items?itemName=ms-vscode-remote.remote-wsl
新增專案 (Hello world!)
重新打開 WSL Ubuntu 並輸入以下指令:
$ mkdir projects
$ cd projects
$ code .
Correct:
安裝 WSL C++ plugin
Install the C++ extension for VSCode: https://marketplace.visualstudio.com/items?itemName=ms-vscode.cpptools
Correct:
In VSCode: Exploer -> New File
輸入 test.cpp

在文字輸入區輸入以下程式碼
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main()
{
vector<string> msg {"Hello", "C++", "World", "from", "VS Code", "and the C++ extension!"};
for (const string& word : msg)
{
cout << word << " ";
}
cout << endl;
}

編譯 & 執行 Hello world!
In VSCode: Terminal -> New Terminal

In VSCode Terminal:
$ g++ test.cpp
$ ./a.out
Hello C++ World from VS Code and the C++ extension!
$
Debugger
可以設置中斷點,方便程式除錯。
launch.json
In VSCode: Exploer -> New Folder
輸入 .vscode

In VSCode: Exploer -> New File
輸入 launch.json
在文字輸入區輸入以下設定檔
{
"version": "0.2.0",
"configurations": [
{
"name": "(gdb) Launch",
"type": "cppdbg",
"request": "launch",
"program": "${workspaceFolder}/a.out",
"args": [],
"stopAtEntry": false,
"cwd": "${workspaceFolder}",
"environment": [],
"externalConsole": false,
"MIMode": "gdb",
"setupCommands": [
{
"description": "Enable pretty-printing for gdb",
"text": "-enable-pretty-printing",
"ignoreFailures": true
}
]
}
]
}
編譯 & 執行 Debugger
In VSCode Terminal:
$ g++ -g test.cpp
$
插入中斷點
在要中斷的程式碼行號左邊點一下

In VSCode: Run -> Start Debugging F5


設定 VSCode 環境 (Windows + mingw)
Modified from: CNOCycle/cpp_tutorial by E. Chen
安裝步驟
- 安裝 Scoop.sh
- 安裝
mingw cmake - 重新開啟 VSCode
圖解說明
安裝 Scoop.sh
In VSCode: Terminal -> New Terminal

在 VSCode Terminal 中輸入:
Invoke-Expression (New-Object System.Net.WebClient).DownloadString('https://get.scoop.sh')
或簡易版指令
iwr -useb get.scoop.sh | iex
Note:
如果遇到錯誤 (execution policy),可能需要使用以下指令更改執行策略後重新執行安裝指令:
Set-ExecutionPolicy RemoteSigned -scope CurrentUser
如果遇到 "無法建立 SSL/TLS 的安全通道。" 問題,可能需要使用以下指令更改系統的 SSL 設定:
[System.Net.ServicePointManager]::SecurityProtocol = "tls12, tls11"
如果遇到 7zip 安裝失敗,可以先安裝 7zip 再安裝 mingw,以下是指令:
scoop install 7zip
scoop install mingw
安裝 mingw cmake
在 VSCode Terminal 中輸入:
scoop install mingw cmake
Note: 安裝完成後須重新啟動 VSCode 才能生效
測試編譯以及除錯
測試編譯
- 在
%USERPROFILE%中新增一個資料夾,名稱可以自由取 (如test)。
Note: 所有的路徑 (包含 %USERPROFILE%) 都不能有非英文的字元,否則 Debugger 會無法執行。
也可以在 %USERPROFILE% 外的資料夾中新增資料夾,如 D:\test。
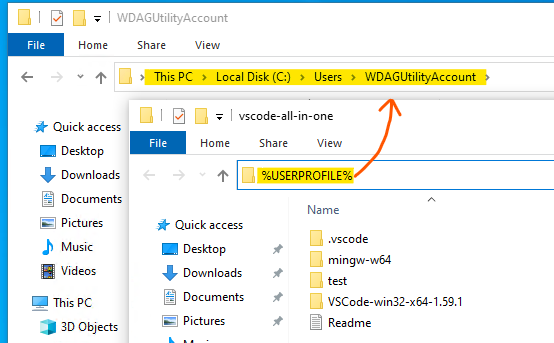
- 用
vscode編輯器選擇開啟新增的資料夾 (以test為例),如下圖示範:
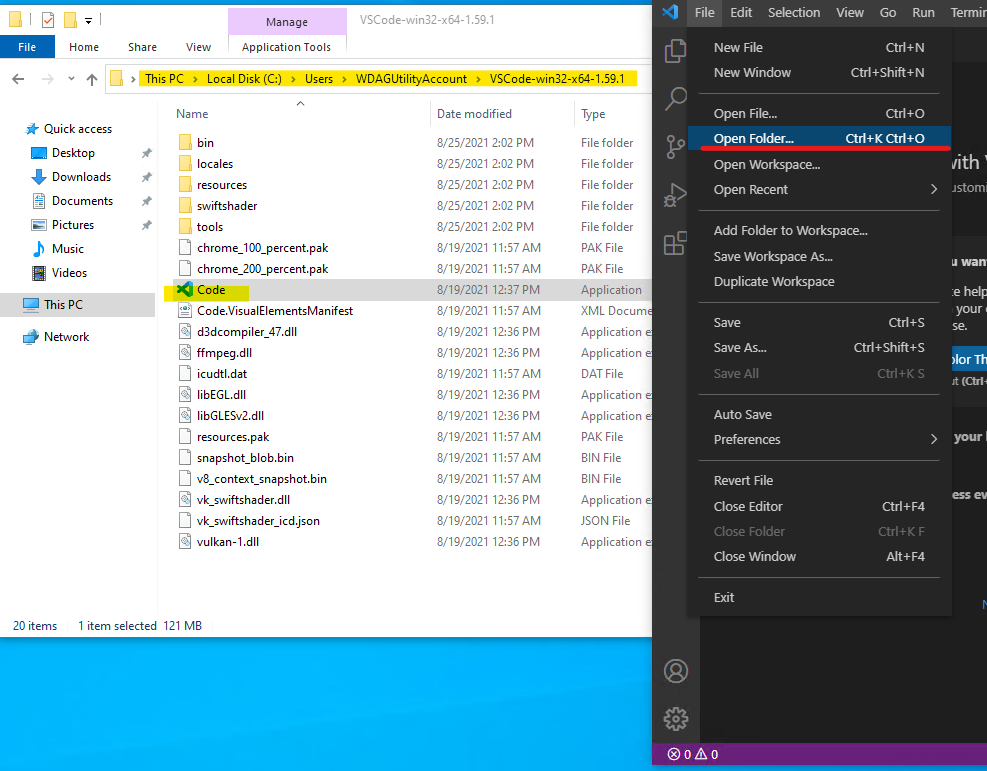
- 信任開啟檔案,選擇
Yes, I trust,如下圖示範:
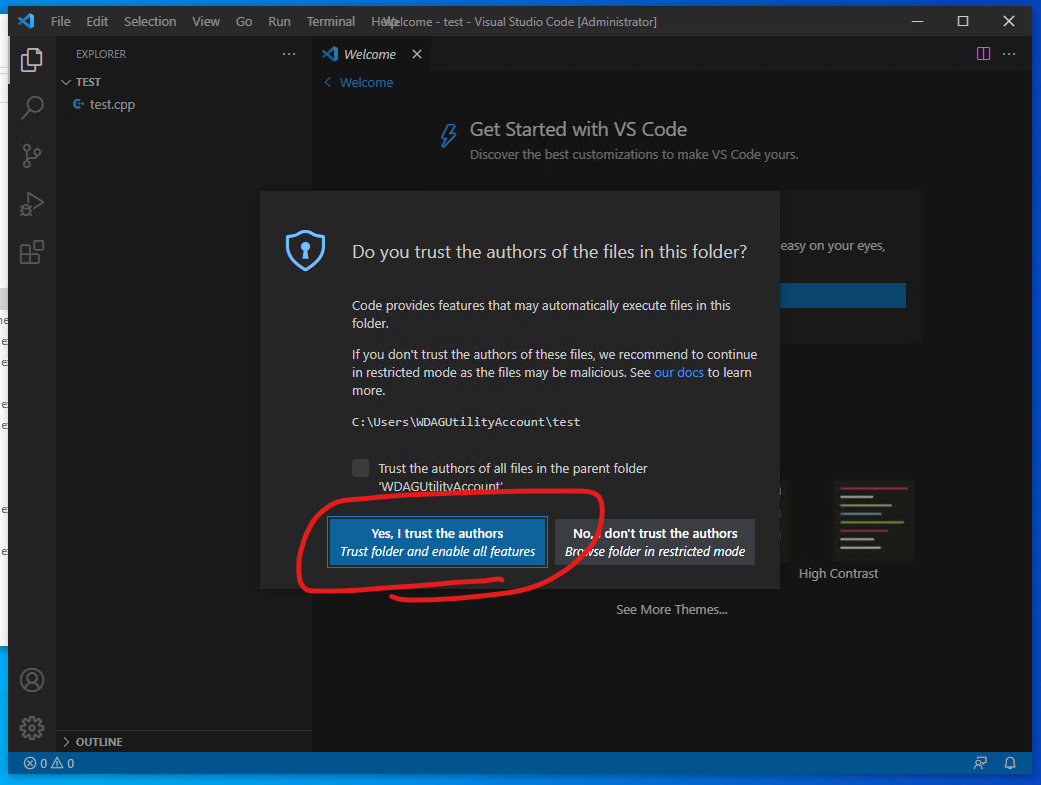
- 新增文件
test.cpp,如下圖示範:
In VSCode: Exploer -> New File
輸入 test.cpp

在文字輸入區輸入以下程式碼
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main()
{
vector<string> msg {"Hello", "C++", "World", "from", "VS Code", "and the C++ extension!"};
for (const string& word : msg)
{
cout << word << " ";
}
cout << endl;
}

- 在第 9 行左側按下去,會出現紅點,如下圖示範:

- 按下
ctrl+shift+B按鍵,或上方terminal -> Run Build Task,如下圖示範:

- 此時上方會出現以下畫面,選擇中間選項使用 g++ 編譯檔案,如下圖示範:

- 設置正確的話,此時下方會出現編譯成功完成的提示,如下圖示範:

測試除錯
-
完成前項
測試編譯的所有流程 -
按下左方三角形按鈕後選擇
Run and Debug,如下圖示範:

- 此時上方會依序出現相關提示,選擇預設的即可,如下圖示範:


- 若設定正確的話,會看到程式停留在選取的第 9 行,如下圖示範:

Reference:
- CNOCycle/cpp_tutorial by E. Chen
- Get Started with C++ and Windows Subsystem for Linux in Visual Studio Code
- Get Started with C++ and Mingw-w64 in Visual Studio Code
Sturcture and Class
Slides version: lecture1_slides.html Website version: lecture1.html
- Recap: Structure
- What is a Class?
- Difference between Class and Structure
- VSCode Tutorial
- Lab 1: Hello Class
Recap: Structure
Example: Structures in C - GeeksforGeeks
// A variable declaration with structure declaration.
struct Point
{
int x, y;
} p1; // The variable p1 is declared with 'Point'
// A variable declaration like basic data types
struct Point
{
int x, y;
};
int main()
{
struct Point p1; // The variable p1 is declared like a normal variable
}
How to Initialize/Modify a Structure
#include <iostream>
using namespace std;
// A variable declaration like basic data types
struct Point
{
int x, y;
};
void init_point(struct Point &p);
void print_point(const struct Point &p);
void modify_point(struct Point &p);
int main()
{
struct Point p1; // The variable p1 is declared like a normal variable
init_point(p1);
print_point(p1);
modify_point(p1);
print_point(p1);
return 0;
}
void init_point(struct Point &p)
{
p.x = 10;
p.y = 20;
}
void print_point(const struct Point &p)
{
std::cout << "(" << p.x << ", " << p.y << ")" << std::endl;
}
void modify_point(struct Point &p)
{
p.x = 100;
p.y = 200;
}
Output (in console):
$ ./a.out
(10, 20)
(100, 200)
What is a Class?
A user-defined datatype which groups together related pieces of information.
-- Introduction to C++ | Electrical Engineering and Computer Science | MIT OpenCourseWare
Example
- Point on a 2D plane
- x-coordinate
- y-coordinate
Definition of Class
class Point
{
public:
// Data members
int x;
int y;
// Member functions
void init();
void print();
void modify();
};
Difference between Class and Structure
Definition
class Point struct Point
{ {
public:
// Data members // Data members
int x; int x;
int y; int y;
// Member functions // No Member functions
void init();
void print();
void modify();
}; };
// Class usuallay don't use // Structure usuallay use
// functions to manipulate // functions to manipulate
// the data members // the data members
void init_point(struct Point &p);
void print_point(const struct Point &p);
void modify_point(struct Point &p);
Usage
int main() int main()
{ {
Point p1; struct Point p1;
p1.init(); init_point(p1);
p1.print(); print_point(p1);
p1.modify(); modify_point(p1);
p1.print(); print_point(p1);
return 0; return 0;
} }
VSCode Tutorial
Lab 1: Hello Class
Lab 1: Class Helloworld
顯示 Complex Class 的數字
- 輸入:無
- 輸出:顯示 Complex Class 的數字
- 檔名:
lab1_<學號>.cpp(e.g.lab1_106062802.cpp)
程式僅需輸出兩 complex 數字 a 及 b 以及 c = a + b 的結果。
Format
(a) = a1 + a2 i
(b) = b1 + b2 i
(c) = a + b = c1 + c2 i
Example
$ ./a.out
(a) = 1 + 2 i
(b) = 3 + -4 i
(c) = (a) + (b) = 4 + -2 i
Pseudo Code
#include <iostream>
using namespace std;
class Complex
{
public:
int real;
int imag;
friend ostream &operator<<(ostream &os, const Complex &c)
{
os << c.real << " + " << c.imag << " i";
return os;
}
void print() const
{
// TODO: implement this function
// Hint: use cout to print the complex number.
// use 'real' and 'imag' as the real and imaginary part
// of the complex number.
}
Complex &operator+(const Complex &c)
{
real += c.real;
imag += c.imag;
return *this;
}
};
int main()
{
Complex a, b, c;
a.real = 1;
a.imag = 2;
cout << "(a) = " << a << endl;
b.real = 3;
b.imag = -4;
cout << "(b) = ";
b.print();
cout << endl;
c = a + b;
cout << "(c) = (a) + (b) = " << c << endl;
return 0;
}
Class Design 101
Slides version: lecture2_slides.html Website version: lecture2.html
- Recap: Hello Class
- Class Definition
- Class Instance
- Class Usage/Member Function
- Example: Triangle
- Example: Vector
Recap: Hello Class
class Point
{
public:
// Data members
int x;
int y;
// Member functions
void init();
void print();
void modify();
};
int main()
{
Point p1;
p1.init();
p1.print();
p1.modify();
p1.print();
return 0;
}
Class Definition
Syntax:
class Point // the class name
{
public: // public data members and member functions
// Note: there is also private: and protected: sections.
// we will discuss them in following lectures
// Data members
// as like as the data in a 'struct', you can have multiple
// variables in different types
int x;
int y;
};
Class Instance
int main()
{
Point p1, p2;
// init 2 instances of Point
p1.x = 0; p1.y = 0;
p2.x = 0; p2.y = 0;
// print 2 instances of Point
cout << "p1: (" << p1.x << ", " << p1.y << ")" << endl;
cout << "p2: (" << p2.x << ", " << p2.y << ")" << endl;
// modify each instance
// p1 and p2 are the same class, but they are different instances
// so they can have different values
p1.x = 1; p1.y = 2;
p2.x = 3; p2.y = 4;
// you can see the change in p1 and p2
cout << "p1: (" << p1.x << ", " << p1.y << ")" << endl;
cout << "p2: (" << p2.x << ", " << p2.y << ")" << endl;
return 0;
}
$ ./a.out
p1: (0, 0)
p2: (0, 0)
p1: (1, 2)
p2: (3, 4)
Class Usage/Member Function
Class as a argument
As like as struct, you can use a class instance as a argument to a function.
void init_point(Point &p)
{
p.x = 0;
p.y = 0;
}
void print_point(const Point &p)
{
cout << "(" << p.x << ", " << p.y << ")";
}
void modify_point(Point &p, const int& arg_x, const int& arg_y)
{
p.x = arg_x;
p.y = arg_y;
}
int main()
{
Point p1, p2;
// init 2 instances of Point
init_point(p1);
init_point(p2);
// print 2 instances of Point
cout << "p1: "; print_point(p1); cout << endl;
cout << "p2: "; print_point(p2); cout << endl;
// modify each instance
modify_point(p1, 1, 2);
modify_point(p2, 3, 4);
// you can see the change in p1 and p2
cout << "p1: "; print_point(p1); cout << endl;
cout << "p2: "; print_point(p2); cout << endl;
return 0;
}
Use class member function
Instead of using extra functions, you can use member functions to manipulate the data.
class Point // the class name
{
public: // public data members and functions
// Note: there is also private: and protected: sections.
// we will discuss them in following lectures
// Data members
// as like as the data in a 'struct', you can have multiple
// variables in different types
int x;
int y;
// Member functions
// different from a 'struct', you can have multiple functions
// in a class that related to the class
void init() { x = 0; y = 0; }
void print() { cout << "(" << x << ", " << y << ")"; }
void modify(const int& arg_x, const int& arg_y) { x = arg_x; y = arg_y; }
};
int main()
{
Point p1, p2;
// init 2 instances of Point
p1.init(); p2.init();
// print 2 instances of Point
p1.print(); p2.print();
// modify each instance
p1.modify(1, 2); p2.modify(3, 4);
// you can see the change in p1 and p2
p1.print(); p2.print();
return 0;
}
Example: Triangle [Source]
#include <iostream>
using namespace std;
class Triangle
{
public:
double x1, y1, x2, y2, x3, y3;
void init();
void print();
void modify(double, double, double, double, double, double);
double area();
};
void Triangle::init()
{
x1 = 0;
y1 = 0;
x2 = 0;
y2 = 0;
x3 = 0;
y3 = 0;
}
void Triangle::print()
{
cout << "Triangle: " << endl;
cout << "(" << x1 << ", " << y1 << ")" << endl;
cout << "(" << x2 << ", " << y2 << ")" << endl;
cout << "(" << x3 << ", " << y3 << ")" << endl;
}
void Triangle::modify(double arg_x1, double arg_y1, double arg_x2,
double arg_y2, double arg_x3, double arg_y3)
{
x1 = arg_x1;
y1 = arg_y1;
x2 = arg_x2;
y2 = arg_y2;
x3 = arg_x3;
y3 = arg_y3;
}
double Triangle::area()
{
return (x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2) / 2;
}
int main()
{
Triangle t;
t.init();
t.print();
t.modify(1, 1, 2, 2, 0, 3);
t.print();
cout << "Area: " << t.area() << endl;
return 0;
}
Output:
$ ./a.out
Triangle:
(0, 0)
(0, 0)
(0, 0)
Triangle:
(1, 1)
(2, 2)
(0, 3)
Area: 1.5
Example: Vector [Source]
#include <iostream>
using namespace std;
class Vector
{
public:
int x, y, z;
void init();
void print();
void modify(int, int, int);
int dot(const Vector &);
Vector cross(const Vector &);
};
void Vector::init()
{
x = 0;
y = 0;
z = 0;
}
void Vector::print()
{
cout << "Vector: "
<< "(" << x << ", " << y << ", " << z << ")";
}
void Vector::modify(int arg_x, int arg_y, int arg_z)
{
x = arg_x;
y = arg_y;
z = arg_z;
}
int Vector::dot(const Vector &arg_v)
{
return x * arg_v.x + y * arg_v.y + z * arg_v.z;
}
Vector Vector::cross(const Vector &arg_v)
{
Vector v;
v.x = y * arg_v.z - z * arg_v.y;
v.y = z * arg_v.x - x * arg_v.z;
v.z = x * arg_v.y - y * arg_v.x;
return v;
}
int main()
{
Vector v1, v2;
v1.init();
v1.print();
cout << endl;
v1.modify(1, 1, 1);
v1.print();
cout << endl;
cout << endl;
v2.init();
v2.print();
cout << endl;
cout << endl;
v2.modify(2, 3, 4);
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Dot: " << v1.dot(v2) << endl;
cout << endl;
v2.modify(5, 6, 7);
Vector v3 = v1.cross(v2);
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Cross: ";
v3.print();
cout << endl;
cout << endl;
return 0;
}
Output:
Vector: (0, 0, 0)
Vector: (1, 1, 1)
Vector: (0, 0, 0)
v1: Vector: (1, 1, 1)
v2: Vector: (2, 3, 4)
Dot: 9
v1: Vector: (1, 1, 1)
v2: Vector: (5, 6, 7)
Cross: Vector: (1, -2, 1)
Pratices
- Pratice 1: 參考
Triangleclass, 如果四邊形、多邊形要如何設計? - Pratice 2: 參考
Vectorclass, 如果需要紀錄多維度的座標系上、或是轉換 basis 為其他 vector 要如何設計?
Example 1: Trangle
#include <iostream>
using namespace std;
class Triangle
{
public:
double x1, y1, x2, y2, x3, y3;
void init();
void print();
void modify(double, double, double, double, double, double);
double area();
};
void Triangle::init()
{
x1 = 0;
y1 = 0;
x2 = 0;
y2 = 0;
x3 = 0;
y3 = 0;
}
void Triangle::print()
{
cout << "Triangle: " << endl;
cout << "(" << x1 << ", " << y1 << ")" << endl;
cout << "(" << x2 << ", " << y2 << ")" << endl;
cout << "(" << x3 << ", " << y3 << ")" << endl;
}
void Triangle::modify(double arg_x1, double arg_y1, double arg_x2,
double arg_y2, double arg_x3, double arg_y3)
{
x1 = arg_x1;
y1 = arg_y1;
x2 = arg_x2;
y2 = arg_y2;
x3 = arg_x3;
y3 = arg_y3;
}
double Triangle::area()
{
return (x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2) / 2;
}
int main()
{
Triangle t;
t.init();
t.print();
t.modify(1, 1, 2, 2, 0, 3);
t.print();
cout << "Area: " << t.area() << endl;
return 0;
}
Example 2: Vector
#include <iostream>
using namespace std;
class Vector
{
public:
int x, y, z;
void init();
void print();
void modify(int, int, int);
int dot(const Vector &);
Vector cross(const Vector &);
};
void Vector::init()
{
x = 0;
y = 0;
z = 0;
}
void Vector::print()
{
cout << "Vector: "
<< "(" << x << ", " << y << ", " << z << ")";
}
void Vector::modify(int arg_x, int arg_y, int arg_z)
{
x = arg_x;
y = arg_y;
z = arg_z;
}
int Vector::dot(const Vector &arg_v)
{
return x * arg_v.x + y * arg_v.y + z * arg_v.z;
}
Vector Vector::cross(const Vector &arg_v)
{
Vector v;
v.x = y * arg_v.z - z * arg_v.y;
v.y = z * arg_v.x - x * arg_v.z;
v.z = x * arg_v.y - y * arg_v.x;
return v;
}
int main()
{
Vector v1, v2;
v1.init();
v1.print();
cout << endl;
v1.modify(1, 1, 1);
v1.print();
cout << endl;
cout << endl;
v2.init();
v2.print();
cout << endl;
cout << endl;
v2.modify(2, 3, 4);
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Dot: " << v1.dot(v2) << endl;
cout << endl;
v2.modify(5, 6, 7);
Vector v3 = v1.cross(v2);
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Cross: ";
v3.print();
cout << endl;
cout << endl;
return 0;
}
Class Data Members & Member Functions
Slides version: lecture3_slides.html Website version: lecture3.html
- Define Class Data Members & Member Functions
public,private,protectedmember- Kickstart of getter & setter
thismember- Variable scope in a class
::scope resolution operator
staticdata member- Kickstart of constructor & destructor
- Example 1: Triangle (again)
- Example 2: Vector (again)
- Example 3: Integer Calculator
Define Class Data Members & Member Functions
- Why do we need data members?
- To store data
- Make data accessible
- Why do we need member functions?
- To perform operations
- Ease of access to data
Design data members
Guidelines:
- each data member should be seen only by its owner
- if you want to access it, you need to use getter & setter (discussed on next lecture)
- if you want a data member to be accessible by other classes, you should handle it carefully
- the naming convention of data members should be consistent, meaningful, and easy to understand
_is used to separate wordsm_is used to indicate a data memberarg_is used to indicate an argument- etc.
Example: Point_2D
#include <iostream>
using namespace std;
class Point_2D // the class name
// we use first upper case letter to indicate a class
{
private: // private data members
// we will discuss it later
// Data members
// we use `m_` to indicate a data member
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
public: // public member functions
// we will discuss in the next lecture
// Member functions
// we use lower case letter to indicate a member function
// also, we just define the function declaration
// and leave the definition to the end of the class
// iniialize the x and y coordinate
void init();
// print the x and y coordinate
void print();
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
void modify(const int &arg_x, const int &arg_y);
};
// function definition
// initialize the x and y coordinate
void Point_2D::init()
{
m_x = 0;
m_y = 0;
}
// print the x and y coordinate
void Point_2D::print()
{
cout << "(" << m_x << ", " << m_y << ")";
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
void Point_2D::modify(const int &arg_x, const int &arg_y)
{
m_x = arg_x;
m_y = arg_y;
}
// main function
int main()
{
Point_2D p1, p2;
// init 2 instances of Point
p1.init(); p2.init();
// print 2 instances of Point
p1.print(); cout << endl;
p2.print(); cout << endl;
// modify each instance
p1.modify(1, 2);
p2.modify(3, 4);
// you can see the change in p1 and p2
p1.print(); cout << endl;
p2.print(); cout << endl;
return 0;
}
Design member functions (discuss on next lecture)
Guidelines:
- each member function should show it's accessibility explicitly
- '_' is used to indicate a member function used internally (
private) - all other functions are public
- '_' is used to indicate a member function used internally (
- essential member functions should be defined in the class
- getter & setter
- constructor & destructor
operator=(disscuss on later lecture)
- etc.
public, private, protected member
To identify the accessibility of a member, we use public, private, and protected keywords.
publicdata members is accessible by other classes.privatedata members is accessible only by its owner.protecteddata members is accessible by other inherited classes and its owner. (discuss in lecture 8)
public member
Same as struct.
class Point // the class name
{
public:
// public data members
// we can access them directly by use `.` operator
int m_x;
int m_y;
};
int main()
{
Point p1;
// init p1
p1.m_x = 1;
p1.m_y = 2;
// print p1
cout << "(" << p1.m_x << ", " << p1.m_y << ")" << endl;
return 0;
}
private member
Different from struct, private member is not accessible by other classes or functions.
#include <iostream>
using namespace std;
// Point_2D class
class Point_2D
{
private: // private data members
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
public: // public member functions
// iniialize the x and y coordinate
void init();
// print the x and y coordinate
void print();
// modify the x and y coordinate
void modify(const int &arg_x, const int &arg_y);
// modify the point by another point
void modify(const Point_2D &arg_point);
};
// Point_2D_2 class
class Point_2D_2
{
private: // private data members
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
public: // public member functions
// iniialize the x and y coordinate
void init();
// print the x and y coordinate
void print();
// modify the x and y coordinate
void modify(const int &arg_x, const int &arg_y);
// modify the point by another point
// NOTE: compile error
void modify(const Point_2D &arg_point);
};
// function definition
// Point_2D class
// initialize the x and y coordinate
void Point_2D::init()
{
m_x = 0;
m_y = 0;
}
// print the x and y coordinate
void Point_2D::print()
{
cout << "(" << m_x << ", " << m_y << ")";
}
// modify the x and y coordinate
void Point_2D::modify(const int &arg_x, const int &arg_y)
{
m_x = arg_x;
m_y = arg_y;
}
// modify the point by another point
void Point_2D::modify(const Point_2D &arg_point)
{
m_x = arg_point.m_x;
m_y = arg_point.m_y;
}
// Point_2D_2 class
// initialize the x and y coordinate
void Point_2D_2::init()
{
m_x = 0;
m_y = 0;
}
// print the x and y coordinate
void Point_2D_2::print()
{
cout << "(" << m_x << ", " << m_y << ")";
}
// modify the x and y coordinate
void Point_2D_2::modify(const int &arg_x, const int &arg_y)
{
m_x = arg_x;
m_y = arg_y;
}
// modify the point by another point
void Point_2D_2::modify(const Point_2D &arg_point)
{
// compile error, error: 'm_x' is a private member of 'Point_2D'
// need to use getter (discuss on the next lecture)
m_x = arg_point.m_x;
m_y = arg_point.m_y;
}
// main function
int main()
{
Point_2D point1;
Point_2D_2 point2;
point1.init();
point2.init();
point1.print(); cout << endl;
point2.print(); cout << endl;
point1.modify(1, 2);
point2.modify(point1);
point1.print(); cout << endl;
point2.print(); cout << endl;
return 0;
}
this data member
To access the data members of current class explicitly, we use this keyword.
Usage: (inside the class definition)
void Point_2D::init()
{
// access the data members of current class
this->m_x = 0;
this->m_y = 0;
}
Example: Point_2D (use this)
#include <iostream>
using namespace std;
class Point_2D
{
private: // private data members
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
public: // public member functions
// iniialize the x and y coordinate
void init();
// print the x and y coordinate
void print();
// modify the x and y coordinate
void modify(const int &arg_x, const int &arg_y);
};
// function definition
// initialize the x and y coordinate
void Point_2D::init()
{
// initialize the x coordinate
// NOTE: this is a pointer to the current object
// so we can use this-> to access the private data member
this->m_x = 0;
// initialize the y coordinate
// NOTE: this-> is equivalent to (*this)
(*this).m_y = 0;
}
// print the x and y coordinate
void Point_2D::print()
{
cout << "(" << this->m_x << ", " << this->m_y << ")";
}
// modify the x and y coordinate
void Point_2D::modify(const int &arg_x, const int &arg_y)
{
this->m_x = arg_x;
this->m_y = arg_y;
}
// main function
int main()
{
Point_2D p1, p2;
// init 2 instances of Point
p1.init(); p2.init();
// print 2 instances of Point
p1.print(); cout << endl;
p2.print(); cout << endl;
// modify each instance
p1.modify(1, 2);
p2.modify(3, 4);
// you can see the change in p1 and p2
p1.print(); cout << endl;
p2.print(); cout << endl;
return 0;
}
Variable scope in a class
Reference: Scope resolution operator in C++ - GeeksforGeeks
- Which variables are accessible in a member function?
- data members
- local variables
- global variables (Ref: Lecture 11: Function & Reference (2))
- function arguments
Example:
#include <iostream>
using namespace std;
int a = 1;
class A
{
public:
int a;
void f()
{
a = a; // how to access global variable a?
}
};
int main()
{
A a;
a.f();
return 0;
}
:: scope resolution operator
Usage: Global variable
// C++ program to show that we can access a global variable
// using scope resolution operator :: when there is a local
// variable with same name
#include <iostream>
using namespace std;
int x; // Global x
int main()
{
int x = 10; // Local x
cout << "Value of global x is " << ::x;
cout << "\nValue of local x is " << x;
return 0;
}
Usage: Function name
// C++ program to show that scope resolution operator :: is used
// to define a function outside a class
#include <iostream>
using namespace std;
class A
{
public:
// Only declaration
void fun();
};
// Definition outside class using ::
void A::fun()
{
cout << "fun() called";
}
int main()
{
A a;
a.fun();
return 0;
}
Example:
#include <iostream>
using namespace std;
int global_a = 1;
// a = 1;
class A
{
public:
int local_a;
// int a;
void f()
{
local_a = ::global_a;
// a = ::a;
}
};
int main()
{
A a;
a.f();
return 0;
}
Case: a class in a class
// Use of scope resolution class inside another class.
#include <iostream>
using namespace std;
class outside
{
public:
int x;
class inside
{
public:
int x;
static int y; // we talk it later
int foo();
};
};
int outside::inside::y = 5;
int main()
{
outside A;
outside::inside B;
}
static data member
Reference: Static Keyword in C++ - GeeksforGeeks
To maintain the status of a class or save memory usage, we use static data member.
Note: the value of a static variable is shared during the entire execution of the program and will initialize only once.
// C++ program to demonstrate
// the use of static Static
// variables in a Function
#include <iostream>
#include <string>
using namespace std;
void demo()
{
// static variable
static int count = 0;
cout << count << " ";
// value is updated and
// will be carried to next
// function calls
count++;
}
int main()
{
for (int i = 0; i < 5; i++)
demo();
return 0;
}
Example: static data member
Note: static data member will share the same value for all instances of the class.
// C++ program to demonstrate static
// variables inside a class
#include <iostream>
using namespace std;
class GfG
{
public:
static int i;
GfG(){
// Default constructor
// we will discuss this in the next lecture
};
};
// static data member should be initialized in global scope
int GfG::i = 1;
int main()
{
GfG obj;
// prints value of i
cout << obj.i;
}
Initialize static data member is important
Without initializing static data member, the compiler will not know the value of static data member.
// C++ program to demonstrate static
// variables inside a class
#include <iostream>
using namespace std;
class GfG
{
public:
static int i;
};
int main()
{
GfG obj;
// prints value of i
cout << obj.i << endl;
}
Example 1: Triangle (again) [Source]
A Triangle:
- contains 3 points
- on the 2D plane
- need to be able to calculate the area
- need to be initialized, printed, and modified
Example 2: Vector (again) [Source]
A Vector:
- contains 3 factors of the 3 basis $\bold{i}$, $\bold{j}$, $\bold{k}$
- need to be able to calculate the length
- need to be able to calculate the dot, cross product
- need to be initialized, printed, and modified
Example 3: Integer Calculator [Source]
A Integer Calculator:
- contains current value, input value, and operation
- neet to be able to set the input value
- neet to be able to set the operation
- neet to be able to calculate the result
- neet to be able to clear the input value
- need to be initialized
- need to be able to get all information
Pratices
- Pratice 1: 參考
Triangleclass, 如果四邊形、多邊形要如何設計要儲存的變數? - Pratice 2: 參考
Vectorclass, 如果需要支援多維度的座標系上、或是轉換 basis 為其他 vector 要如何設計儲存的變數? - Pratice 3: 參考
Integer Calculatorclass, 如果需要支援M+運算要如何設計相關變數?
Example 1: Trangle
#include <iostream>
using namespace std;
// Triangle class declaration
class Triangle
{
private:
// define three points of the triangle
// in x1, y1, x2, y2, x3, y3 format
double m_x1, m_y1, m_x2, m_y2, m_x3, m_y3;
public:
// initialize the triangle
void init();
// print the triangle
void print();
// modify the three points of the triangle
void modify(double, double, double,
double, double, double);
// calculate the area of the triangle
double area();
};
// Triangle class implementation
// initialize the triangle
void Triangle::init()
{
// initialize the three points of the triangle
m_x1 = 0.0;
m_y1 = 0.0;
m_x2 = 1.0;
m_y2 = 0.0;
m_x3 = 0.0;
m_y3 = 1.0;
}
// print the triangle
void Triangle::print()
{
// print the three points of the triangle
cout << "Triangle: " << endl;
cout << "(" << m_x1 << ", " << m_y1 << ")" << endl;
cout << "(" << m_x2 << ", " << m_y2 << ")" << endl;
cout << "(" << m_x3 << ", " << m_y3 << ")" << endl;
}
// modify the three points of the triangle
void Triangle::modify(double arg_x1, double arg_y1,
double arg_x2, double arg_y2,
double arg_x3, double arg_y3)
{
// modify the three points of the triangle
m_x1 = arg_x1;
m_y1 = arg_y1;
m_x2 = arg_x2;
m_y2 = arg_y2;
m_x3 = arg_x3;
m_y3 = arg_y3;
}
// calculate the area of the triangle
double Triangle::area()
{
// calculate the area of the triangle
return (m_x1 * (m_y2 - m_y3) + m_x2 * (m_y3 - m_y1) + m_x3 * (m_y1 - m_y2)) / 2.0;
}
// main function
int main()
{
Triangle t;
t.init();
t.print();
t.modify(1, 1, 2, 2, 0, 3);
t.print();
cout << "Area: " << t.area() << endl;
return 0;
}
Example 2: Vector
#include <iostream>
#include <cmath>
using namespace std;
// Vector class declaration
class Vector
{
private:
// define the three factor of the basis vectors
// on the x, y, z axes
double m_x, m_y, m_z;
public:
// initialize the vector
void init();
// print the vector
void print();
// modify the three factor of the basis vectors
void modify(double, double, double);
// calculate the length of the vector
double length();
// calculate the dot product of two vectors
int dot(const Vector &);
// calculate the cross product of two vectors
Vector cross(const Vector &);
};
// initialize the vector
void Vector::init()
{
// initialize the three factor of the basis vectors
m_x = 0.0;
m_y = 0.0;
m_z = 0.0;
}
// print the vector
void Vector::print()
{
// print the three factor of the basis vectors
cout << "Vector: " << endl;
cout << "(" << m_x << ", " << m_y << ", " << m_z << ")" << endl;
}
// modify the three factor of the basis vectors
void Vector::modify(double arg_x, double arg_y, double arg_z)
{
// modify the three factor of the basis vectors
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
// calculate the length of the vector
double Vector::length()
{
// calculate the length of the vector
return sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
}
// calculate the dot product of two vectors
int Vector::dot(const Vector &arg_v)
{
// calculate the dot product of two vectors
return m_x * arg_v.m_x + m_y * arg_v.m_y + m_z * arg_v.m_z;
}
// calculate the cross product of two vectors
Vector Vector::cross(const Vector &arg_v)
{
// calculate the cross product of two vectors
Vector v;
v.m_x = m_y * arg_v.m_z - m_z * arg_v.m_y;
v.m_y = m_z * arg_v.m_x - m_x * arg_v.m_z;
v.m_z = m_x * arg_v.m_y - m_y * arg_v.m_x;
return v;
}
// main function
int main()
{
Vector v1, v2;
v1.init();
v1.print();
cout << endl;
cout << "Length of v1: " << v1.length() << endl;
v1.modify(1, 1, 1);
v1.print();
cout << endl;
cout << "Length of v1: " << v1.length() << endl;
cout << endl;
v2.init();
v2.print();
cout << endl;
cout << "Length of v2: " << v2.length() << endl;
v2.modify(2, 3, 4);
v2.print();
cout << endl;
cout << "Length of v2: " << v2.length() << endl;
cout << endl;
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Dot: " << v1.dot(v2) << endl;
cout << endl;
v2.modify(5, 6, 7);
Vector v3 = v1.cross(v2);
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Cross: ";
v3.print();
cout << endl;
cout << endl;
return 0;
}
Example 3: Integer Calculator
#include <iostream>
using namespace std;
// Triangle class declaration
class Int_Calc
{
private:
// define current value
long m_curr_val;
// define input value
long m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and ` ` for none
char m_op;
// calculate result
void _calc_result(); // private function, discuss in the next lecture
public:
// clear the input value
void clear();
// clear the entire class
void init();
// set the input value
void set_input(long arg_input);
// add the input value to the current value
void add();
// subtract the input value from the current value
void sub();
// multiply the input value with the current value
void mul();
// divide the current value by the input value
void div();
// assign the input value to the current value
void assign();
// get the current value
long get_curr_val();
// get the current operation
char get_op();
// get the input value
long get_input_val();
};
// Int_Calc class implementation
// calculate the result
void Int_Calc::_calc_result()
{
switch (m_op)
{
case '+':
m_curr_val += m_input_val;
break;
case '-':
m_curr_val -= m_input_val;
break;
case '*':
m_curr_val *= m_input_val;
break;
case '/':
m_curr_val /= m_input_val;
break;
case ' ':
m_curr_val = m_input_val;
break;
default:
break;
}
}
// clear the input value
void Int_Calc::clear()
{
m_input_val = 0;
}
// clear the entire class
void Int_Calc::init()
{
m_curr_val = 0;
m_input_val = 0;
m_op = ' ';
}
// set the input value
void Int_Calc::set_input(long arg_input)
{
m_input_val = arg_input;
}
// add the input value to the current value
void Int_Calc::add()
{
_calc_result();
m_op = '+';
}
// subtract the input value from the current value
void Int_Calc::sub()
{
_calc_result();
m_op = '-';
}
// multiply the input value with the current value
void Int_Calc::mul()
{
_calc_result();
m_op = '*';
}
// divide the current value by the input value
void Int_Calc::div()
{
_calc_result();
m_op = '/';
}
// assign the input value to the current value
void Int_Calc::assign()
{
_calc_result();
m_op = ' ';
}
// get the current value
long Int_Calc::get_curr_val()
{
return m_curr_val;
}
// get the current operation
char Int_Calc::get_op()
{
return m_op;
}
// get the input value
long Int_Calc::get_input_val()
{
return m_input_val;
}
// main function
int main()
{
// create an instance of the class
Int_Calc calc;
// initialize the class
calc.init();
// set the input value
calc.set_input(10);
// get the input value
cout << calc.get_input_val() << endl;
// add the input value to the current value
calc.add();
// get current op
cout << '\'' << calc.get_op() << '\'' << endl;
// set another input value
calc.set_input(20);
// get the input value
cout << calc.get_input_val() << endl;
// clear the input value
calc.clear();
// set the input value
calc.set_input(30);
// get the input value
cout << calc.get_input_val() << endl;
// compute the result
calc.assign();
// print the result
cout << calc.get_curr_val() << endl;
}
Class Constructor & Modifer
Slides version: lecture4_slides.html Website version: lecture4.html
- Define Class Data Members & Member Functions (again)
- How to initialize and modify class members?
- Class constructor & copy constructor
- Class getter & setter
- Access
public,private, members
- Access
- Class destructor
constfunction &constclass instance- Member function & Global function
- How to design class interface?
- Example: Triangle (again)
- Example: Vector (again)
- Example: Integer Calculator (again)
- Lab 4: Complex Number
Define Class Data Members & Member Functions
- Why do we need data members?
- To store data
- Make data accessible
- Why do we need member functions?
- To perform operations
- Ease of access to data
Design member functions
Guidelines:
- each member function should show it's accessibility explicitly
- '_' is used to indicate a member function used internally (
private) - all other functions are public
- '_' is used to indicate a member function used internally (
- essential member functions should be defined in the class
- getter & setter
- constructor & destructor
operator=(disscuss on later lecture)- etc.
- utility functions are usually for in-class use
- utility functions are used to help other member functions and make it reusable, readable, and maintainable
- naming of member functions should be consistent with the class name
get_for getterset_for setteris_for predicatehas_for predicateadd_for mutatorremove_for mutatorclear_for mutatorsize_for predicateto_string_for predicatefrom_string_for mutator- etc.
Example: Point_2D
#include <iostream>
using namespace std;
class Point_2D // the class name
// we use first upper case letter to indicate a class
{
private: // private data members & member functions
// Data members
// we use `m_` to indicate a data member
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
// Member functions
// we use `_` to indicate a member function
// check if the point is valid
void _check_validity();
public: // public member functions
// Constructor
// Constructor & Default constructor
// initialize data members, with default values
// accessable to const object by default
Point_2D(const int &arg_x = 0, const int &arg_y = 0);
// Copy constructor
// copy the data members from the given object
// accessable to const object by default
Point_2D(const Point_2D &arg_point);
// Destructor
~Point_2D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// Member functions
// we use lower case letter to indicate a member function
// also, we just define the function declaration
// and leave the definition to the end of the class
// print the x and y coordinate in format (x, y)
// accessable to const object
void print() const;
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void set_x(const int &arg_x);
void set_y(const int &arg_y);
void set(const int &arg_x, const int &arg_y);
// get the x coordinate and y coordinate
// accessable to const object
int get_x() const;
int get_y() const;
};
// function definition
// check if the point is valid
void Point_2D::_check_validity()
{
// check if the x coordinate is valid
if (m_x < 0)
{
// if not, set it to 0
m_x = 0;
}
// check if the y coordinate is valid
if (m_y < 0)
{
// if not, set it to 0
m_y = 0;
}
}
// Constructor & Default constructor
// initialize data members, with default values
Point_2D::Point_2D(const int &arg_x, const int &arg_y)
// use `: var_name1(arg_var_name1), var_name2(arg_var_name2)`
// to initialize data members
: m_x(arg_x),
m_y(arg_y)
{
// check if the point is valid
_check_validity();
}
// Copy constructor
// copy the data members from the given object
Point_2D::Point_2D(const Point_2D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y)
{
// check if the point is valid
_check_validity();
}
// print the x and y coordinate
// accessable to const object
void Point_2D::print() const
{
cout << "(" << m_x << ", " << m_y << ")";
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_2D::set_x(const int &arg_x)
{
m_x = arg_x;
// check if the point is valid
_check_validity();
}
void Point_2D::set_y(const int &arg_y)
{
m_y = arg_y;
// check if the point is valid
_check_validity();
}
void Point_2D::set(const int &arg_x, const int &arg_y)
{
m_x = arg_x;
m_y = arg_y;
// check if the point is valid
_check_validity();
}
// get the x coordinate and y coordinate
// accessable to const object
int Point_2D::get_x() const
{
return m_x;
}
int Point_2D::get_y() const
{
return m_y;
}
// main function
int main()
{
// create a Point_2D object with initial values
Point_2D p1(1, 2);
// or create with another Point_2D object
Point_2D p2(p1);
// print 2 instances of Point
p1.print();
cout << endl;
// or use getter
cout << "(" << p2.get_x() << ", "
<< p2.get_y() << ")" << endl;
// modify each instance with setter
p1.set(3, 4);
p2.set_x(5);
p2.set_y(6);
// you can see the change in p1 and p2
p1.print();
cout << endl;
// or use getter
cout << "(" << p2.get_x() << ", "
<< p2.get_y() << ")" << endl;
return 0;
}
How to initialize and modify class members?
- To initialize class members, we use constructor.
- The constructor is a function that is called when an object is created.
- To modify class members, we use setter.
- The setter is a function that is called when we want to modify the value of a class member.
Class constructor & copy constructor
- The constructor is a function that is called when an object is created.
- 3 types of constructor
- constructor with no arguments
- usally used to initialize data members with default values
- constructor with arguments
- usally used to initialize data members with given values
- constructor with another same-type object (copy constructor)
- usally used to copy data members from another object
- constructor with no arguments
Syntax:
class class_name
{
public:
// default constructor
class_name();
// constructor with arguments
class_name(int arg_x, int arg_y);
// constructor with arguments that has default value
// the usage is the same as the default constructor
class_name(int arg_x = 0, int arg_y = 0);
// copy constructor
class_name(const class_name &arg_class_name);
};
Example: Point_2D (partial)
public: // public member functions
// Constructor
// Constructor & Default constructor
// initialize data members, with default values
// accessable to const object by default
Point_2D(const int &arg_x = 0, const int &arg_y = 0);
// Copy constructor
// copy the data members from the given object
// accessable to const object by default
Point_2D(const Point_2D &arg_point);
// Destructor
~Point_2D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// Constructor & Default constructor
// initialize data members, with default values
Point_2D::Point_2D(const int &arg_x, const int &arg_y)
// use `: var_name1(arg_var_name1), var_name2(arg_var_name2)`
// to initialize data members
: m_x(arg_x),
m_y(arg_y)
{
// check if the point is valid
_check_validity();
}
// Copy constructor
// copy the data members from the given object
Point_2D::Point_2D(const Point_2D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y)
{
// check if the point is valid
_check_validity();
}
Class getter & setter
- The getter is a function that is called when we want to access the value of a class member.
- The setter is a function that is called when we want to modify the value of a class member.
- Getter and setter will check if the value is valid.
Example: Point_2D (partial)
class Point_2D
{
private: // private data members & member functions
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
public: // public member functions
// Setter
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void set_x(const int &arg_x);
void set_y(const int &arg_y);
void set(const int &arg_x, const int &arg_y);
// Getter
// get the x coordinate and y coordinate
// accessable to const object
int get_x() const;
int get_y() const;
};
Class destructor
- The destructor is a function that is called when an object is destroyed.
- The destructor is usually used to free the memory that is allocated by the constructor.
Syntax:
class class_name
{
public:
// default constructor
class_name();
// destructor
~class_name();
};
const function & const class instance
- How to access the member of a class that is declared as
const?- add
constto the class declaration
- add
Example: Point_2D (partial)
class Point_2D
{
private: // private data members & member functions
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
public: // public member functions
// print the x and y coordinate in format (x, y)
// we add `const` so that it can access the value form a const object
void print() const;
// Setter
// modify the x and y coordinate
// we don't add `const` because it will modify the value
void set_x(const int &arg_x);
void set_y(const int &arg_y);
void set(const int &arg_x, const int &arg_y);
// Getter
// get the x coordinate and y coordinate
// we add `const` so that it can access the value form a const object
int get_x() const;
int get_y() const;
};
// main function
int main()
{
// create a Point_2D object with initial values
Point_2D p1(1, 2);
// also create a `const` Point_2D object
const Point_2D p2(3, 4);
// create a `const` with another Point_2D object
const Point_2D p3(p1);
// print 3 instances of Point
p1.print();
cout << endl;
// getter can be used to access the member of a `const` object
cout << "(" << p2.get_x() << ", "
<< p2.get_y() << ")" << endl;
// also `print()` can be used to access the member of a `const` object
p3.print();
cout << endl;
// modify each instance with setter
p1.set(3, 4);
p2.set_x(5); // error, cannot modify the member of a `const` object
p2.set_y(6); // error, cannot modify the member of a `const` object
return 0;
}
Member function & Global function
Rather than design a member function in a class, we can design a global function to process a class instance.
- Member function usually process the data members of a class.
- public: getter, setter, constructor, destructor, etc.
- private: utility functions, debug functions, etc.
- Global function usually process class instances with member functions.
- like normal function.
- but friend function can access the member of a class. (discuss in the next lecture)
Example: Point_2D
#include <iostream>
using namespace std;
class Point_2D // the class name
// we use first upper case letter to indicate a class
{
private: // private data members & member functions
// Data members
// we use `m_` to indicate a data member
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
// Private member functions
// we use `_` to indicate a private member function
// utility: check if the point is valid
void _check_validity();
public: // public member functions
// Constructor
// Constructor & Default constructor
// initialize data members, with default values
// accessable to const object by default
Point_2D(const int &arg_x = 0, const int &arg_y = 0);
// Copy constructor
// copy the data members from the given object
// accessable to const object by default
Point_2D(const Point_2D &arg_point);
// Destructor
~Point_2D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// Member functions
// we use lower case letter to indicate a member function
// also, we just define the function declaration
// and leave the definition to the end of the class
// print the x and y coordinate in format (x, y)
// accessable to const object
void print() const;
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void set_x(const int &arg_x);
void set_y(const int &arg_y);
void set(const int &arg_x, const int &arg_y);
// get the x coordinate and y coordinate
// accessable to const object
int get_x() const;
int get_y() const;
};
How to design class interface?
- To design a class interface, we need to know the following:
- What is the interface of the class?
- What is the input?
- What is the output?
- What is the return value?
- How to implement the interface?
- How to use the interface?
- How to call the interface?
- What is the interface of the class?
- Usually have guidelines in a team to design the interface.
- To simplify it, we can use the following guidelines for the course.
Guidelines: (again)
- each member function should show it's accessibility explicitly
- '_' is used to indicate a member function used internally (
private) - all other functions are public
- '_' is used to indicate a member function used internally (
- essential member functions should be defined in the class
- getter & setter
- constructor & destructor
operator=(disscuss on later lecture)- etc.
- utility functions are usually for in-class use
- utility functions are used to help other member functions and make it reusable, readable, and maintainable
- naming of member functions should be consistent with the class name
get_for getterset_for setteris_for predicatehas_for predicateadd_for mutatorremove_for mutatorclear_for mutatorsize_for predicateto_string_for predicatefrom_string_for mutator- etc.
Example 1: Triangle (again) [Source]
A Triangle:
- contains 3 points
- on the 2D plane
- need to be able to calculate the area
- need to be initialized, printed, and modified
Example 2: Vector (again) [Source]
A Vector:
- contains 3 factors of the 3 basis $\bold{i}$, $\bold{j}$, $\bold{k}$
- need to be able to calculate the length
- need to be able to calculate the dot, cross product
- need to be initialized, printed, and modified
Example 3: Integer Calculator (again) [Source]
A Integer Calculator:
- contains current value, input value, and operation
- neet to be able to set the input value
- neet to be able to set the operation
- neet to be able to calculate the result
- neet to be able to clear the input value
- need to be initialized
- need to be able to get all information
Lab 4: Complex Number
Example 1: Trangle
#include <iostream>
using namespace std;
// Triangle class declaration
class Triangle
{
private:
// define three points of the triangle
// in x1, y1, x2, y2, x3, y3 format
double m_x1, m_y1, m_x2, m_y2, m_x3, m_y3;
// check & correct the triangle points to counterclockwise order
void _check_points();
public:
// Constructor
Triangle(const double &arg_x1 = 0.0, const double &arg_y1 = 0.0,
const double &arg_x2 = 0.0, const double &arg_y2 = 0.0,
const double &arg_x3 = 0.0, const double &arg_y3 = 0.0);
// Copy constructor
Triangle(const Triangle &arg_triangle);
// Destructor
~Triangle()
{
// do nothing
}
// print the triangle
void print();
// modify the three points of the triangle
void set_points(const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2,
const double &arg_x3, const double &arg_y3);
void set_point1(const double &arg_x1, const double &arg_y1);
void set_point2(const double &arg_x2, const double &arg_y2);
void set_point3(const double &arg_x3, const double &arg_y3);
void set_x1(const double &arg_x1);
void set_y1(const double &arg_y1);
void set_x2(const double &arg_x2);
void set_y2(const double &arg_y2);
void set_x3(const double &arg_x3);
void set_y3(const double &arg_y3);
// get the three points of the triangle
double get_x1() const;
double get_y1() const;
double get_x2() const;
double get_y2() const;
double get_x3() const;
double get_y3() const;
// calculate the area of the triangle
double area();
};
// Triangle class implementation
// check & correct the triangle points to counterclockwise order
void Triangle::_check_points()
{
// calculate the area of the triangle
double area = (m_x1 * (m_y2 - m_y3) + m_x2 * (m_y3 - m_y1)
+ m_x3 * (m_y1 - m_y2)) / 2.0;
// if the area is negative, swap the points
if (area < 0.0)
{
double temp_x = m_x1;
double temp_y = m_y1;
m_x1 = m_x2;
m_y1 = m_y2;
m_x2 = temp_x;
m_y2 = temp_y;
}
}
// Constructor
Triangle::Triangle(const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2,
const double &arg_x3, const double &arg_y3)
: m_x1(arg_x1), m_y1(arg_y1), m_x2(arg_x2), m_y2(arg_y2),
m_x3(arg_x3), m_y3(arg_y3)
{
// check & correct the triangle points to counterclockwise order
_check_points();
}
// Copy constructor
Triangle::Triangle(const Triangle &arg_triangle)
: m_x1(arg_triangle.m_x1), m_y1(arg_triangle.m_y1),
m_x2(arg_triangle.m_x2), m_y2(arg_triangle.m_y2),
m_x3(arg_triangle.m_x3), m_y3(arg_triangle.m_y3)
{
}
// print the triangle
void Triangle::print()
{
// print the three points of the triangle
cout << "Triangle: " << endl;
cout << "(" << m_x1 << ", " << m_y1 << ")" << endl;
cout << "(" << m_x2 << ", " << m_y2 << ")" << endl;
cout << "(" << m_x3 << ", " << m_y3 << ")" << endl;
}
// set the three points of the triangle
void Triangle::set_points(const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2,
const double &arg_x3, const double &arg_y3)
{
m_x1 = arg_x1;
m_y1 = arg_y1;
m_x2 = arg_x2;
m_y2 = arg_y2;
m_x3 = arg_x3;
m_y3 = arg_y3;
// check & correct the triangle points to counterclockwise order
_check_points();
}
void Triangle::set_point1(const double &arg_x1, const double &arg_y1)
{
m_x1 = arg_x1;
m_y1 = arg_y1;
// check & correct the triangle points to counterclockwise order
_check_points();
}
void Triangle::set_point2(const double &arg_x2, const double &arg_y2)
{
m_x2 = arg_x2;
m_y2 = arg_y2;
// check & correct the triangle points to counterclockwise order
_check_points();
}
void Triangle::set_point3(const double &arg_x3, const double &arg_y3)
{
m_x3 = arg_x3;
m_y3 = arg_y3;
// check & correct the triangle points to counterclockwise order
_check_points();
}
void Triangle::set_x1(const double &arg_x1)
{
m_x1 = arg_x1;
// check & correct the triangle points to counterclockwise order
_check_points();
}
void Triangle::set_y1(const double &arg_y1)
{
m_y1 = arg_y1;
// check & correct the triangle points to counterclockwise order
_check_points();
}
void Triangle::set_x2(const double &arg_x2)
{
m_x2 = arg_x2;
// check & correct the triangle points to counterclockwise order
_check_points();
}
void Triangle::set_y2(const double &arg_y2)
{
m_y2 = arg_y2;
// check & correct the triangle points to counterclockwise order
_check_points();
}
void Triangle::set_x3(const double &arg_x3)
{
m_x3 = arg_x3;
// check & correct the triangle points to counterclockwise order
_check_points();
}
void Triangle::set_y3(const double &arg_y3)
{
m_y3 = arg_y3;
// check & correct the triangle points to counterclockwise order
_check_points();
}
// get the three points of the triangle
double Triangle::get_x1() const
{
return m_x1;
}
double Triangle::get_y1() const
{
return m_y1;
}
double Triangle::get_x2() const
{
return m_x2;
}
double Triangle::get_y2() const
{
return m_y2;
}
double Triangle::get_x3() const
{
return m_x3;
}
double Triangle::get_y3() const
{
return m_y3;
}
// calculate the area of the triangle
double Triangle::area()
{
// calculate the area of the triangle
return (m_x1 * (m_y2 - m_y3) + m_x2 * (m_y3 - m_y1) + m_x3 * (m_y1 - m_y2)) / 2.0;
}
// main function
int main()
{
Triangle t(1, 1, 2, 2, 0, 3);
t.print();
cout << "Area: " << t.area() << endl;
// change the points of the triangle
t.set_points(1, 2, 2, 3, 3, 1);
t.print();
cout << "Area: " << t.area() << endl;
return 0;
}
Example 2: Vector
#include <iostream>
#include <cmath>
using namespace std;
// Vector class declaration
class Vector
{
private:
// define the three factor of the basis vectors
// on the x, y, z axes
double m_x, m_y, m_z;
public:
// Constructor
Vector(const double &arg_x = 0.0, const double &arg_y = 0.0,
const double &arg_z = 0.0);
// Copy constructor
Vector(const Vector &arg_vector);
// Destructor
~Vector()
{
// do nothing
}
// print the vector
void print();
// set the three factor of the basis vectors
void set_vector(const double &arg_x, const double &arg_y,
const double &arg_z);
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
// get the three factor of the basis vectors
double get_x() const;
double get_y() const;
double get_z() const;
// calculate the length of the vector
double length();
// calculate the dot product of two vectors
int dot(const Vector &);
// calculate the cross product of two vectors
Vector cross(const Vector &);
};
// Vector class implementation
// Constructor
Vector::Vector(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x), m_y(arg_y), m_z(arg_z)
{
}
// Copy constructor
Vector::Vector(const Vector &arg_vector)
: m_x(arg_vector.m_x), m_y(arg_vector.m_y), m_z(arg_vector.m_z)
{
}
// print the vector
void Vector::print()
{
// print the three factor of the basis vectors
cout << "Vector: " << endl;
cout << "(" << m_x << ", " << m_y << ", " << m_z << ")" << endl;
}
// set the three factor of the basis vectors
void Vector::set_vector(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
void Vector::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Vector::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Vector::set_z(const double &arg_z)
{
m_z = arg_z;
}
// get the three factor of the basis vectors
double Vector::get_x() const
{
return m_x;
}
double Vector::get_y() const
{
return m_y;
}
double Vector::get_z() const
{
return m_z;
}
// calculate the length of the vector
double Vector::length()
{
// calculate the length of the vector
return sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
}
// calculate the dot product of two vectors
int Vector::dot(const Vector &arg_v)
{
// calculate the dot product of two vectors
return m_x * arg_v.m_x + m_y * arg_v.m_y + m_z * arg_v.m_z;
}
// calculate the cross product of two vectors
Vector Vector::cross(const Vector &arg_v)
{
// calculate the cross product of two vectors
Vector v;
v.m_x = m_y * arg_v.m_z - m_z * arg_v.m_y;
v.m_y = m_z * arg_v.m_x - m_x * arg_v.m_z;
v.m_z = m_x * arg_v.m_y - m_y * arg_v.m_x;
return v;
}
// main function
int main()
{
Vector v1;
v1.print();
cout << endl;
cout << "Length of v1: " << v1.length() << endl;
v1.set_vector(1.0, 2.0, 3.0);
v1.print();
cout << endl;
cout << "Length of v1: " << v1.length() << endl;
cout << endl;
Vector v2(v1);
v2.print();
cout << endl;
cout << "Length of v2: " << v2.length() << endl;
v2.set_vector(2.0, 3.0, 4.0);
v2.print();
cout << endl;
cout << "Length of v2: " << v2.length() << endl;
cout << endl;
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Dot: " << v1.dot(v2) << endl;
cout << endl;
v2.set_vector(1.0, 1.0, 1.0);
Vector v3(v1.cross(v2));
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Cross: ";
v3.print();
cout << endl;
cout << endl;
return 0;
}
Example 3: Integer Calculator
#include <iostream>
using namespace std;
// Triangle class declaration
class Int_Calc
{
private:
// define current value
long m_curr_val;
// define input value
long m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and ` ` for none
char m_op;
// calculate result
void _calc_result();
public:
// Constructor
Int_Calc(const long &arg_curr_val = 0, const long &arg_input_val = 0,
const char &arg_op = ' ');
// Copy constructor
Int_Calc(const Int_Calc &arg_int_calc);
// Destructor
~Int_Calc()
{
// do nothing
}
// clear the input value
void clear();
// set the input value
void set_input(long arg_input);
// add the input value to the current value
void add();
// subtract the input value from the current value
void sub();
// multiply the input value with the current value
void mul();
// divide the current value by the input value
void div();
// assign the input value to the current value
void assign();
// get the current value
long get_curr_val();
// get the current operation
char get_op();
// get the input value
long get_input_val();
};
// Int_Calc class implementation
// Constructor
Int_Calc::Int_Calc(const long &arg_curr_val, const long &arg_input_val,
const char &arg_op)
: m_curr_val(arg_curr_val), m_input_val(arg_input_val), m_op(arg_op)
{
}
// Copy constructor
Int_Calc::Int_Calc(const Int_Calc &arg_int_calc)
: m_curr_val(arg_int_calc.m_curr_val),
m_input_val(arg_int_calc.m_input_val),
m_op(arg_int_calc.m_op)
{
}
// calculate the result
void Int_Calc::_calc_result()
{
switch (m_op)
{
case '+':
m_curr_val += m_input_val;
break;
case '-':
m_curr_val -= m_input_val;
break;
case '*':
m_curr_val *= m_input_val;
break;
case '/':
m_curr_val /= m_input_val;
break;
case ' ':
m_curr_val = m_input_val;
break;
default:
break;
}
}
// clear the input value
void Int_Calc::clear()
{
m_input_val = 0;
}
// set the input value
void Int_Calc::set_input(long arg_input)
{
m_input_val = arg_input;
}
// add the input value to the current value
void Int_Calc::add()
{
_calc_result();
m_op = '+';
}
// subtract the input value from the current value
void Int_Calc::sub()
{
_calc_result();
m_op = '-';
}
// multiply the input value with the current value
void Int_Calc::mul()
{
_calc_result();
m_op = '*';
}
// divide the current value by the input value
void Int_Calc::div()
{
_calc_result();
m_op = '/';
}
// assign the input value to the current value
void Int_Calc::assign()
{
_calc_result();
m_op = ' ';
}
// get the current value
long Int_Calc::get_curr_val()
{
return m_curr_val;
}
// get the current operation
char Int_Calc::get_op()
{
return m_op;
}
// get the input value
long Int_Calc::get_input_val()
{
return m_input_val;
}
// main function
int main()
{
// create an instance of the class
Int_Calc calc;
// set the input value
calc.set_input(10);
// get the input value
cout << calc.get_input_val() << endl;
// add the input value to the current value
calc.add();
// get current op
cout << '\'' << calc.get_op() << '\'' << endl;
// set another input value
calc.set_input(20);
// get the input value
cout << calc.get_input_val() << endl;
// clear the input value
calc.clear();
// set the input value
calc.set_input(30);
// get the input value
cout << calc.get_input_val() << endl;
// compute the result
calc.assign();
// print the result
cout << calc.get_curr_val() << endl;
}
Lab 4: Complex Number
Lab 4-1: Complex Numbers (50%)
- 輸入:
- 以
double格式輸入複數的實數及虛數部分,以空格分開 - 一行輸入一個複數
- 輸入 Ctrl+D 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
^Z) 再輸入 Enter 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
- 以
- 輸出:
- 顯示複數儲存 Complex Class 的數字
- 一行輸入跟著輸出一個複數
- 檔名:
lab4-1_<學號>.cpp(e.g.lab4-1_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果
- 請使用 pseudo code 提供的 main function 來處理輸入與輸出
- 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Format
<real 1> <imag 1>⏎
<real 1> + <imag 1> i
<real 2> <imag 2>⏎
<real 2> + <imag 2> i
...
<real n> <imag n>⏎
<real n> + <imag n> i
^Z⏎
Example
$ ./a.out
1.0 0.0⏎
1 + 0 i
2.0 1.1⏎
2 + 1.1 i
-3.0 -2.2⏎
-3 + -2.2 i
^Z⏎
$
Pseudo Code
#include <iostream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
public:
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
// print function
// note: be careful about the format of output
// especially the ` ` and newline (endl)
void print();
};
int main()
{
double real = 0.0, imag = 0.0;
while (cin >> real >> imag)
{
Complex c(real, imag);
c.print();
}
return 0;
}
Reference Code:
陳光齊 (110021102)
#include <iostream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex(double arg_real, double arg_imag);
// print function
// note: be careful about the format of output
// especially the ` ` and newline (endl)
void print();
};
Complex::Complex(double arg_real, double arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
void Complex::print()
{
cout << m_real << " + " << this->m_imag << " i" << endl;
}
int main()
{
double real = 0.0, imag = 0.0;
while (cin >> real >> imag)
{
Complex c(real, imag);
c.print();
}
return 0;
}
賴杰弘 (110021118)
#include <iostream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy Constructor
Complex(const Complex &arg_complex);
// Destructor
~Complex(){
// do nothing
};
// print function
// note: be careful about the format of output
// especially the ` ` and newline (endl)
void print();
};
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
Complex::Complex(const Complex &arg_complex)
: m_real(arg_complex.m_real), m_imag(arg_complex.m_imag)
{
}
void Complex::print()
{
cout << m_real << " + " << m_imag << " i" << endl;
return;
}
int main()
{
double real = 0.0, imag = 0.0;
while (cin >> real >> imag)
{
Complex c(real, imag);
c.print();
}
return 0;
}
Lab 4-2: Complex Number Calculation (35%)
- 輸入:
- 以
double格式輸入複數的實數及虛數部分,以空格分開,一行輸入一個複數 - 以
char格式輸入複數的運算子,包含+、-、*、/,一行輸入一個運算子 - 複數與運算子以交錯的方式輸入,一行輸入一個複數接著一個運算子,倒數兩行為複數與完成輸入指令
- 輸入 Ctrl+D 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
^Z) 再輸入 Enter (Format 中的⏎) 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
- 以
- 輸出:
- 顯示運算複數的結果
- 檔名:
lab4-2_<學號>.cpp(e.g.lab4-2_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果
- 使用者不需要處理錯誤輸入
- 請使用 pseudo code 提供的 main function 來處理輸入與輸出
- 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Format
<real 1> <imag 1>⏎
<op 1>⏎
<real 2> <imag 2>⏎
<op 2>⏎
...
<real n-1> <imag n-1>⏎
<op n-1>⏎
<real n> <imag n>⏎
^Z⏎
<real result> + <imag result> i
Example
$ ./a.out
1.0 0.0⏎
^Z⏎
1 + 0 i
$
$ ./a.out
1.0 0.0⏎
+⏎
2.0 1.1⏎
-⏎
-3.0 -2.2⏎
*⏎
4.3 2.1⏎
/⏎
-1.2 -3.4⏎
^Z⏎
-8.74846 + 2.46231 i
$
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
public:
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
// print function
// note: be careful about the format of output
// especially the ` ` and newline (endl)
void print();
// add function
// subtract function
// multiply function
// divide function
};
int main()
{
string input;
Complex result_complex;
char op = ' ';
while (getline(cin, input))
{
// input is a operation
if (input == "+" || input == "-" || input == "*" || input == "/")
{
op = input[0];
continue;
}
// input is a complex number
else
{
stringstream ss(input);
double real, imag;
ss >> real >> imag;
Complex current_complex(real, imag);
switch (op)
{
case '+':
result_complex = result_complex.add(current_complex);
break;
case '-':
result_complex = result_complex.sub(current_complex);
break;
case '*':
result_complex = result_complex.mul(current_complex);
break;
case '/':
result_complex = result_complex.div(current_complex);
break;
case ' ':
result_complex = current_complex;
break;
default:
cerr << "Error: unknown operation" << endl;
return 1;
}
}
}
result_complex.print();
return 0;
}
Reference Code:
陳光齊 (110021102)
#include <iostream>
#include <sstream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex(double arg_real = 0.0, double arg_imag = 0.0);
Complex(const Complex &arg_c);
// print function
// note: be careful about the format of output
// especially the ` ` and newline (endl)
void print() const;
double get_real() const;
double get_imag() const;
void set_real(double &real);
void set_imag(double &imag);
Complex add(const Complex &arg_c);
Complex sub(const Complex &arg_c);
Complex mul(const Complex &arg_c);
Complex div(Complex &arg_c);
Complex const_mul(double arg_x);
Complex conj();
};
Complex::Complex(double arg_real, double arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.get_real()), m_imag(arg_c.get_imag())
{
}
void Complex::print() const
{
cout << m_real << " + " << this->m_imag << " i" << endl;
}
double Complex::get_real() const
{
return m_real;
}
double Complex::get_imag() const
{
return m_imag;
}
void Complex::set_real(double &real)
{
m_real = real;
}
void Complex::set_imag(double &imag)
{
m_imag = imag;
}
Complex Complex::add(const Complex &arg_c)
{
Complex c_temp;
c_temp.m_real = m_real + (arg_c.get_real());
c_temp.m_imag = m_imag + (arg_c.get_imag());
return c_temp;
}
Complex Complex::sub(const Complex &arg_c)
{
Complex c_temp;
c_temp.m_real = m_real - (arg_c.get_real());
c_temp.m_imag = m_imag - (arg_c.get_imag());
return c_temp;
}
Complex Complex::mul(const Complex &arg_c)
{
Complex c_temp;
c_temp.m_real = m_real * (arg_c.get_real()) - m_imag * (arg_c.get_imag());
c_temp.m_imag = m_imag * (arg_c.get_real()) + m_real * (arg_c.get_imag());
return c_temp;
}
Complex Complex::div(Complex &arg_c)
{
double c = arg_c.get_real();
double d = arg_c.get_imag();
Complex c_this(m_real, m_imag);
Complex c_temp;
arg_c = arg_c.conj();
c_temp = c_this.mul(arg_c);
c = c * c + d * d;
c = 1 / c;
c_temp = c_temp.const_mul(c);
return c_temp;
}
Complex Complex::const_mul(double arg_x)
{
Complex c_temp;
c_temp.m_real = m_real * arg_x;
c_temp.m_imag = m_imag * arg_x;
return c_temp;
}
Complex Complex::conj()
{
Complex c_temp;
c_temp.m_real = m_real;
c_temp.m_imag = -m_imag;
return c_temp;
}
int main()
{
string input;
Complex result_complex;
char op = ' ';
while (getline(cin, input))
{
// input is a operation
if (input == "+" || input == "-" || input == "*" || input == "/")
{
op = input[0];
continue;
}
// input is a complex number
else
{
stringstream ss(input);
double real, imag;
ss >> real >> imag;
Complex current_complex(real, imag);
switch (op)
{
case '+':
result_complex = result_complex.add(current_complex);
break;
case '-':
result_complex = result_complex.sub(current_complex);
break;
case '*':
result_complex = result_complex.mul(current_complex);
break;
case '/':
result_complex = result_complex.div(current_complex);
break;
case ' ':
result_complex = current_complex;
break;
default:
cerr << "Error: unknown operation" << endl;
return 1;
}
}
}
result_complex.print();
return 0;
}
賴杰弘 (110021118)
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy Constructor
Complex(const Complex &arg_complex);
// Destructor
~Complex(){
// do nothing
};
// print function
// note: be careful about the format of output
// especially the ` ` and newline (endl)
void print();
// add function
Complex add(const Complex &arg_complex);
// subtract function
Complex sub(const Complex &arg_complex);
// multiply function
Complex mul(const Complex &arg_complex);
// divide function
Complex div(const Complex &arg_complex);
};
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
Complex::Complex(const Complex &arg_complex)
: m_real(arg_complex.m_real), m_imag(arg_complex.m_imag)
{
}
void Complex::print()
{
cout << m_real << " + " << m_imag << " i" << endl;
return;
}
Complex Complex::add(const Complex &arg_complex)
{
Complex complex;
complex.m_real = m_real + arg_complex.m_real;
complex.m_imag = m_imag + arg_complex.m_imag;
return complex;
}
Complex Complex::sub(const Complex &arg_complex)
{
Complex complex;
complex.m_real = m_real - arg_complex.m_real;
complex.m_imag = m_imag - arg_complex.m_imag;
return complex;
}
Complex Complex::mul(const Complex &arg_complex)
{
Complex complex;
complex.m_real = (m_real * arg_complex.m_real) - (m_imag * arg_complex.m_imag);
complex.m_imag = (m_real * arg_complex.m_imag) + (m_imag * arg_complex.m_real);
return complex;
}
Complex Complex::div(const Complex &arg_complex)
{
Complex complex;
complex.m_real = ((m_real * arg_complex.m_real) + (m_imag * arg_complex.m_imag))
/ ((arg_complex.m_real * arg_complex.m_real) + (arg_complex.m_imag * arg_complex.m_imag));
complex.m_imag = ((m_imag * arg_complex.m_real) - (m_real * arg_complex.m_imag))
/ ((arg_complex.m_real * arg_complex.m_real) + (arg_complex.m_imag * arg_complex.m_imag));
return complex;
}
int main()
{
string input;
Complex result_complex;
char op = ' ';
while (getline(cin, input))
{
// input is a operation
if (input == "+" || input == "-" || input == "*" || input == "/")
{
op = input[0];
continue;
}
// input is a complex number
else
{
stringstream ss(input);
double real, imag;
ss >> real >> imag;
Complex current_complex(real, imag);
switch (op)
{
case '+':
result_complex = result_complex.add(current_complex);
break;
case '-':
result_complex = result_complex.sub(current_complex);
break;
case '*':
result_complex = result_complex.mul(current_complex);
break;
case '/':
result_complex = result_complex.div(current_complex);
break;
case ' ':
result_complex = current_complex;
break;
default:
cerr << "Error: unknown operation" << endl;
return 1;
}
}
}
result_complex.print();
return 0;
}
Lab 4-3: Advance Complex Number Calculation (15%)
- 輸入:
- 以
double格式輸入複數的實數及虛數部分,以空格分開,一行輸入一個複數 - 以
char格式輸入複數的運算子,包含+、-、*、/,一行輸入一個運算子 - 複數與運算子以交錯的方式輸入,一行輸入一個複數接著一個運算子,倒數兩行為複數與完成輸入指令
- 輸入 Ctrl+D 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
^Z) 再輸入 Enter (Format 中的⏎) 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
- 程式輸入以行為單位,每行輸入為任何有效的
string格式
- 以
- 輸出:
- 顯示運算複數的結果
- 若使用者輸入的複數或運算子不正確,則顯示錯誤訊息
Error: Invalid input並結束程式
- 檔名:
lab4-3_<學號>.cpp(e.g.lab4-3_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果或錯誤訊息
- 程式僅需處裡輸入錯誤的例外狀況,如輸入的複數或運算子不正確,其餘錯誤不須處裡
- 請基於 pseudo code 提供的 main function 進行修改來處理輸入與輸出
- 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Format
<real 1> <imag 1>⏎
<op 1>⏎
<real 2> <imag 2>⏎
<op 2>⏎
...
<real n-1> <imag n-1>⏎
<op n-1>⏎
<real n> <imag n>⏎
^Z⏎
<real result> + <imag result> i
Example
Normal
$ ./a.out
1.0 0.0⏎
^Z⏎
1 + 0 i
$
$ ./a.out
1.0 0.0⏎
+⏎
2.0 1.1⏎
-⏎
-3.0 -2.2⏎
*⏎
4.3 2.1⏎
/⏎
-1.2 -3.4⏎
^Z⏎
-8.74846 + 2.46231 i
$
Exception Handling
$ ./a.out
+⏎
Error: Invalid input
$
$ ./a.out
1.0 0.0⏎
+⏎
^Z⏎
Error: Invalid input
$
$ ./a.out
1.0 0.0⏎
1.0 0.0⏎
Error: Invalid input
$
$ ./a.out
1.0 0.0⏎
+⏎
+⏎
Error: Invalid input
$
$ ./a.out
^Z⏎
Error: Invalid input
$
$ ./a.out
1.0 2.0 3.0⏎
Error: Invalid input
$
$ ./a.out
1.0 2.0⏎
sdafsdagret⏎
Error: Invalid input
$
$ ./a.out
sdoifjwepoirjpwoie⏎
Error: Invalid input
$
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
public:
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
// print function
// note: be careful about the format of output
// especially the ` ` and newline (endl)
void print();
// add function
// subtract function
// multiply function
// divide function
// parse function
// note: use `stringstream` and `>>` to parse the string to double
// and use `stringstream::fail()` to check the conversion is successful
};
// parse op global function
char parse_op(const string &arg_str);
// prompt invalid input and exit
void prompt_invalid_input()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
int main()
{
string input;
Complex result_complex;
char op = ' '; // default op is ' '
bool is_process_continue = true; // current process should be continued or not
while (is_process_continue)
{
// get the first input
// check is not end of input
if (input.empty() || cin.eof())
{
prompt_invalid_input();
}
// check the input is a valid complex number
// calculate the result
// get the second input
// check is end of input or not
if (input.empty() || cin.eof())
{
is_process_continue = false;
}
// if not end of input, check the input is a valid operator
}
result_complex.print();
return 0;
}
Reference Code:
藍珮芳(110021116)
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
using namespace std;
class Complex
{
private:
double m_real;
double m_imag;
public:
Complex(double arg_real = 0.0, double arg_imag = 0.0)
{
m_real = arg_real;
m_imag = arg_imag;
}
void print()
{
cout << m_real << " + " << m_imag << " i\n";
};
Complex add(Complex &arg_c)
{
Complex temp;
temp.m_real = m_real + arg_c.m_real;
temp.m_imag = m_imag + arg_c.m_imag;
return temp;
};
Complex sub(Complex &arg_c)
{
Complex temp;
temp.m_real = m_real - arg_c.m_real;
temp.m_imag = m_imag - arg_c.m_imag;
return temp;
};
Complex mul(Complex &arg_c)
{
Complex temp;
temp.m_real = m_real * arg_c.m_real - m_imag * arg_c.m_imag;
temp.m_imag = m_real * arg_c.m_imag + m_imag * arg_c.m_real;
return temp;
};
Complex div(Complex &arg_c)
{
Complex temp;
temp.m_real = (m_real * arg_c.m_real + m_imag * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
temp.m_imag = (m_imag * arg_c.m_real - m_real * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
return temp;
};
};
bool check_complex(string &input)
{
string temp_str;
vector<string> vec;
stringstream terms_extractor(input);
while (terms_extractor >> temp_str)
{
vec.push_back(temp_str);
}
if (vec.size() == 2)
{
if ((!isdigit(vec[0][0]) && vec[0][0] != '-')
|| (!isdigit(vec[1][0]) && vec[1][0] != '-'))
{
return false;
}
for (int i = 1; i < vec[0].size(); i++)
{
if (isdigit(vec[0][i]) || vec[0][i] == '.')
{
continue;
}
else
{
return false;
}
}
for (int i = 1; i < vec[1].size(); i++)
{
if (isdigit(vec[1][i]) || vec[1][i] == '.')
{
continue;
}
else
{
return false;
}
}
}
else
{
return false;
}
return true;
}
bool check_op(string &input)
{
if (input == "+" || input == "-" || input == "*" || input == "/")
{
return true;
}
else
{
return false;
}
}
int main()
{
string input;
Complex result_complex;
char op = ' ';
int process = 0;
while (getline(cin, input))
{
if ((process % 2 == 1) && (check_op(input) == true))
{
op = input[0];
}
else if ((process % 2 == 0) && (check_complex(input) == true))
{
double real, imag;
stringstream ss(input);
ss >> real >> imag;
Complex current_complex(real, imag);
switch (op)
{
case '+':
result_complex = result_complex.add(current_complex);
break;
case '-':
result_complex = result_complex.sub(current_complex);
break;
case '*':
result_complex = result_complex.mul(current_complex);
break;
case '/':
result_complex = result_complex.div(current_complex);
break;
case ' ':
result_complex = current_complex;
break;
default:
cerr << "Error: unknown operation\n";
return 1;
}
}
else
{
cout << "Error: Invalid input" << endl;
return 0;
}
process = process + 1;
}
if (process = 0 || process % 2 == 1)
{
result_complex.print();
}
else
{
cout << "Error: Invalid input" << endl;
}
return 0;
}
TA
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
void prompt_invalid_input();
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0)
{
m_real = arg_real;
m_imag = arg_imag;
}
// print function
// note: be careful about the format of output
// especially the ` ` and newline (endl)
void print()
{
cout << m_real << " + " << m_imag << " i" << endl;
}
// add function
Complex add(const Complex &arg_c)
{
Complex c;
c.m_real = m_real + arg_c.m_real;
c.m_imag = m_imag + arg_c.m_imag;
return c;
}
// subtract function
Complex sub(const Complex &arg_c)
{
Complex c;
c.m_real = m_real - arg_c.m_real;
c.m_imag = m_imag - arg_c.m_imag;
return c;
}
// multiply function
Complex mul(const Complex &arg_c)
{
Complex c;
c.m_real = m_real * arg_c.m_real - m_imag * arg_c.m_imag;
c.m_imag = m_real * arg_c.m_imag + m_imag * arg_c.m_real;
return c;
}
// divide function
Complex div(const Complex &arg_c)
{
if (arg_c.m_real == 0 && arg_c.m_imag == 0)
prompt_invalid_input();
Complex c;
c.m_real = (m_real * arg_c.m_real + m_imag * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
c.m_imag = (m_imag * arg_c.m_real - m_real * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
return c;
}
// parse function
// note: use `stringstream` and `>>` to parse the string to double
// and use `stringstream::fail()` to check the conversion is successful
bool parse(const string &arg_str)
{
// Check if the number of tokens = 2
for (int i = 0, n = 0; i < arg_str.length(); i++)
{
if (arg_str[i] == ' ')
n++;
if (n > 1 || (n == 0 && i == arg_str.length() - 1))
return false;
}
stringstream ss(arg_str);
double input_real, input_imag;
ss >> input_real;
if (ss.fail())
{
return false;
}
ss >> input_imag;
if (ss.fail())
{
return false;
}
m_real = input_real;
m_imag = input_imag;
return ss.eof();
}
};
// parse op global function
char parse_op(const string &arg_str)
{
switch (arg_str[0])
{
case '+':
case '-':
case '*':
case '/':
return arg_str[0];
default:
return '\0'; // invalid op
}
}
// prompt invalid input and exit
void prompt_invalid_input()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
int main()
{
string input;
Complex result_complex;
char op = ' '; // default op is ' '
bool is_process_continue = true; // current process should be continued or not
while (is_process_continue)
{
// get the first input
getline(cin, input);
// check is not end of input
if (input.empty() || cin.eof())
{
prompt_invalid_input();
}
// check the input is a valid complex number
Complex input_complex;
bool is_valid_complex = input_complex.parse(input);
if (!is_valid_complex)
{
prompt_invalid_input();
}
// calculate the result
switch (op)
{
case '+':
result_complex = result_complex.add(input_complex);
break;
case '-':
result_complex = result_complex.sub(input_complex);
break;
case '*':
result_complex = result_complex.mul(input_complex);
break;
case '/':
result_complex = result_complex.div(input_complex);
break;
case ' ':
result_complex = input_complex;
break;
default:
prompt_invalid_input();
}
// get the second input
getline(cin, input);
// check is end of input or not
if (input.empty() || cin.eof())
{
is_process_continue = false;
}
// if not end of input, check the input is a valid operator
else
{
op = parse_op(input);
if (op == '\0')
{
prompt_invalid_input();
}
}
}
result_complex.print();
return 0;
}
Collaborate with Other Classes
Slides version: lecture5_slides.html Website version: lecture5.html
- Interaction in other classes
- How to use a class with another class
- as an argument
- use member functions
- use
friendclass
- How to use a class in another function
- use getter and setter
- use
friendfunction
friendfunction- syntax & example
- Example
- Example: Triangle (again)
- Example: Vector (again)
- Example: Fixed Point Number & Fixed Point Number Calculator
- Pratices
Interaction with other classes
User can use multiple classes to process data.
- use
std::vectorto store multiplestd::stringdata - compute the intersection of a line and a point in a 2D plane with user-defined
lineandpointclasses - etc.
How to use a class in another class
To use a class with another class:
- as an argument
- use member functions
friendclass
Use a class as an argument
Example: Point_2D and Line_2D (v1, partial)
#include <iostream>
using namespace std;
class Point_2D // a point on a 2D plane
{
private:
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
public:
// Constructor
Point_2D(const int &arg_x = 0, const int &arg_y = 0);
Point_2D(const Point_2D &arg_point);
// Member functions
void set_x(const int &arg_x);
void set_y(const int &arg_y);
void set(const int &arg_x, const int &arg_y);
int get_x() const;
int get_y() const;
};
class Line_2D // a line on a 2D plane
{
private:
// record the start point
Point_2D m_start;
// record the end point
Point_2D m_end;
public:
// Constructor
Line_2D(const Point_2D &arg_start, const Point_2D &arg_end);
Line_2D(const Line_2D &arg_line);
// Member functions
void set_start(const Point_2D &arg_start);
void set_end(const Point_2D &arg_end);
void set(const Point_2D &arg_start, const Point_2D &arg_end);
Point_2D get_start() const;
Point_2D get_end() const;
};
Use member functions of a class
Example: Point_2D and Line_2D (v2, partial)
class Line_2D // a line on a 2D plane
{
private:
// record the start point
Point_2D m_start;
// record the end point
Point_2D m_end;
public:
// Constructor
Line_2D(const Point_2D &arg_start, const Point_2D &arg_end);
Line_2D(const Line_2D &arg_line);
// use Point_2D's constructor to set the start and end point
Line_2D(int arg_start_x = 0, int arg_start_y = 0,
int arg_end_x = 0, int arg_end_y = 0);
// Member functions
void set_start(const Point_2D &arg_start);
void set_end(const Point_2D &arg_end);
void set(const Point_2D &arg_start, const Point_2D &arg_end);
// use member function to set the x and y coordinates
void set_start(int arg_x, int arg_y)
{
m_start.set_x(arg_x);
m_start.set_y(arg_y);
}
void set_end(int arg_x, int arg_y)
{
m_end.set_x(arg_x);
m_end.set_y(arg_y);
}
void set(int arg_start_x, int arg_start_y,
int arg_end_x, int arg_end_y)
{
m_start.set_x(arg_start_x);
m_start.set_y(arg_start_y);
m_end.set_x(arg_end_x);
m_end.set_y(arg_end_y);
}
Point_2D get_start() const;
Point_2D get_end() const;
// use member function to get the x and y coordinates
int get_start_x() const { return m_start.get_x(); }
int get_start_y() const { return m_start.get_y(); }
int get_end_x() const { return m_end.get_x(); }
int get_end_y() const { return m_end.get_y(); }
};
Use friend class
Example: Point_2D and Line_2D (v3, partial)
#include <iostream>
using namespace std;
class Point_2D // a point on a 2D plane
{
private:
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
public:
// Constructor
Point_2D(const int &arg_x = 0, const int &arg_y = 0);
Point_2D(const Point_2D &arg_point);
// Member functions
void set_x(const int &arg_x);
void set_y(const int &arg_y);
void set(const int &arg_x, const int &arg_y);
int get_x() const;
int get_y() const;
// Friend class, can access private members
friend class Line_2D;
};
class Line_2D // a line on a 2D plane
{
private:
// record the start point
Point_2D m_start;
// record the end point
Point_2D m_end;
public:
// Constructor
Line_2D(const Point_2D &arg_start, const Point_2D &arg_end);
Line_2D(const Line_2D &arg_line);
// use Point_2D's constructor to set the start and end point
Line_2D(int arg_start_x = 0, int arg_start_y = 0,
int arg_end_x = 0, int arg_end_y = 0);
// Member functions
void set_start(const Point_2D &arg_start);
void set_end(const Point_2D &arg_end);
void set(const Point_2D &arg_start, const Point_2D &arg_end);
// set the x and y coordinates directly because of friend class
void set_start(int arg_x, int arg_y)
{
m_start.m_x = arg_x; m_start.m_y = arg_y;
}
void set_end(int arg_x, int arg_y)
{
m_end.m_x = arg_x; m_end.m_y = arg_y;
}
void set(int arg_start_x, int arg_start_y,
int arg_end_x, int arg_end_y)
{
m_start.m_x = arg_start_x; m_start.m_y = arg_start_y;
m_end.m_x = arg_end_x; m_end.m_y = arg_end_y;
}
Point_2D get_start() const;
Point_2D get_end() const;
// get the x and y coordinates directly because of friend class
int get_start_x() const { return m_start.m_x; }
int get_start_y() const { return m_start.m_y; }
int get_end_x() const { return m_end.m_x; }
int get_end_y() const { return m_end.m_y; }
};
What is a friend class & friend function?
Ref: Friend class and function in C++ - GeeksforGeeks
A friend class can access private and protected members of other class in which it is declared as friend. It is sometimes useful to allow a particular class to access private members of other class.
Friend Class Example
#include <iostream>
class A {
private:
int a;
public:
A() { a = 0; }
friend class B; // Friend Class
};
class B {
private:
int b;
public:
void showA(A& x)
{
// Since B is friend of A, it can access
// private members of A
std::cout << "A::a=" << x.a;
}
};
int main()
{
A a;
B b;
b.showA(a);
return 0;
}
Friend Function Example
#include <iostream>
class B; // Forward declaration, used in class A
class A {
public:
void showB(B&);
};
class B {
private:
int b;
public:
B() { b = 0; }
friend void A::showB(B& x); // Friend function
};
void A::showB(B& x)
{
// Since showB() is friend of B, it can
// access private members of B
std::cout << "B::b = " << x.b;
}
int main()
{
A a;
B x;
a.showB(x);
return 0;
}
Friend Function Example (global)
#include <iostream>
class A {
int a;
public:
A() { a = 0; }
// global friend function
friend void showA(A&);
};
void showA(A& x)
{
// Since showA() is a friend, it can access
// private members of A
std::cout << "A::a=" << x.a;
}
int main()
{
A a;
showA(a);
return 0;
}
How to use a class in another function
To use a class with another function:
- use getter and setter
- use
friendfunction
Use getter and setter of a class
Example: compare two Point_2D objects
int compare(const Point_2D &arg_point1, const Point_2D &arg_point2)
{
// compare the x coordinates
if (arg_point1.get_x() < arg_point2.get_x())
{
return -1;
}
else if (arg_point1.get_x() > arg_point2.get_x())
{
return 1;
}
else
{
// compare the y coordinates
if (arg_point1.get_y() < arg_point2.get_y())
{
return -1;
}
else if (arg_point1.get_y() > arg_point2.get_y())
{
return 1;
}
else
{
return 0;
}
}
}
Use friend function
Example: compare two Point_2D objects with friend function
#include <iostream>
using namespace std;
class Point_2D // a point on a 2D plane
{
private:
// record the x coordinate
int m_x;
// record the y coordinate
int m_y;
public:
// Constructor
Point_2D(const int &arg_x = 0, const int &arg_y = 0);
Point_2D(const Point_2D &arg_point);
// Member functions
void set_x(const int &arg_x);
void set_y(const int &arg_y);
void set(const int &arg_x, const int &arg_y);
int get_x() const;
int get_y() const;
// Friend function, can access private members
friend int compare(const Point_2D &arg_point1, const Point_2D &arg_point2);
};
int compare(const Point_2D &arg_point1, const Point_2D &arg_point2)
{
// compare the x coordinates
if (arg_point1.m_x < arg_point2.m_x)
{
return -1;
}
else if (arg_point1.m_x > arg_point2.m_x)
{
return 1;
}
else
{
// compare the y coordinates
if (arg_point1.m_y < arg_point2.m_y)
{
return -1;
}
else if (arg_point1.m_y > arg_point2.m_y)
{
return 1;
}
else
{
return 0;
}
}
}
Example 1: Triangle (again) [Source]
A Triangle:
- contains 3 points
- on the 2D plane
- need to be able to calculate the area
- need to be initialized, printed, and modified
Example 2: Vector (again) [Source]
A Vector:
- contains 3 factors of the 3 basis $\bold{i}$, $\bold{j}$, $\bold{k}$
- need to be able to calculate the length
- need to be able to calculate the dot, cross product
- need to be initialized, printed, and modified
Example 3: Fixed Point Number & Fixed Point Number Calculator [Source]
A Fixed Point Number:
- contains a integer part, a fractional part, and a precision
- need to be able to calculate the sum, difference
- need to be able to convert to/from string,
float, anddouble - need to be initialized, printed, and modified
A Fixed Point Number Calculator:
- contains current value, input value, and operation
- need to be able to set the input value
- need to be able to set the operation
- need to be able to calculate the result
- need to be able to clear the input value
- need to be initialized
- need to be able to get all information
Pratices
- Pratice 1: 參考
Triangleclass, 如果需要支援多維度的座標系以及四邊形等其他圖形需要如何修改? - Pratice 2: 參考
Vectorclass, 如果需要支援多維度的座標系上、或是轉換 basis 為其他 vector 要如何修改? - Pratice 3: 參考
Fp_Calcclass, 如果需要支援乘除法、超過Fixed_Point可儲存的範圍要如何設計相關的 member function?
Example 1: Trangle
#include <iostream>
using namespace std;
class Triangle_2D; // forward declaration
class Point_2D // the class name
// we use first upper case letter to indicate a class
{
private: // private data members & member functions
// Data members
// we use `m_` to indicate a data member
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// Member functions
// we use `_` to indicate a member function
// check if the point is valid
void _check_validity();
public: // public member functions
// Constructor
// Constructor & Default constructor
// initialize data members, with default values
// accessable to const object by default
Point_2D(const double &arg_x = 0, const double &arg_y = 0);
// Copy constructor
// copy the data members from the given object
// accessable to const object by default
Point_2D(const Point_2D &arg_point);
// Destructor
~Point_2D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// Member functions
// we use lower case letter to indicate a member function
// also, we just define the function declaration
// and leave the definition to the end of the class
// print the x and y coordinate in format (x, y)
// accessable to const object
void print() const;
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set(const double &arg_x, const double &arg_y);
// get the x coordinate and y coordinate
// accessable to const object
double get_x() const;
double get_y() const;
// friend class
friend class Triangle_2D;
};
// Triangle_2D class declaration
class Triangle_2D
{
private:
// define three points of the Triangle_2D
// in array of Point_2D format
Point_2D m_point[3];
// check & correct the Triangle_2D points to counterclockwise order
void _check_points();
public:
// Constructor
Triangle_2D(const double &arg_x0 = 0.0, const double &arg_y0 = 0.0,
const double &arg_x1 = 0.0, const double &arg_y1 = 0.0,
const double &arg_x2 = 0.0, const double &arg_y2 = 0.0);
// Copy constructor
Triangle_2D(const Triangle_2D &arg_triangle);
// Destructor
~Triangle_2D()
{
// do nothing
}
// print the Triangle_2D
void print();
// modify the three points of the Triangle_2D
void set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2);
void set_point1(const double &arg_x0, const double &arg_y0);
void set_point2(const double &arg_x1, const double &arg_y1);
void set_point3(const double &arg_x2, const double &arg_y2);
void set_x0(const double &arg_x0);
void set_y0(const double &arg_y0);
void set_x1(const double &arg_x1);
void set_y1(const double &arg_y1);
void set_x2(const double &arg_x2);
void set_y2(const double &arg_y2);
// get the three points of the Triangle_2D
double get_x0() const;
double get_y0() const;
double get_x1() const;
double get_y1() const;
double get_x2() const;
double get_y2() const;
// calculate the area of the Triangle_2D
double area();
};
// function definition
// check if the point is valid
void Point_2D::_check_validity()
{
// check if the x coordinate is valid
if (m_x < 0)
{
// if not, set it to 0
m_x = 0;
}
// check if the y coordinate is valid
if (m_y < 0)
{
// if not, set it to 0
m_y = 0;
}
}
// Constructor & Default constructor
// initialize data members, with default values
Point_2D::Point_2D(const double &arg_x, const double &arg_y)
// use `: var_name1(arg_var_name1), var_name2(arg_var_name2)`
// to initialize data members
: m_x(arg_x),
m_y(arg_y)
{
// check if the point is valid
_check_validity();
}
// Copy constructor
// copy the data members from the given object
Point_2D::Point_2D(const Point_2D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y)
{
// check if the point is valid
_check_validity();
}
// print the x and y coordinate
// accessable to const object
void Point_2D::print() const
{
cout << "(" << m_x << ", " << m_y << ")";
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_2D::set_x(const double &arg_x)
{
m_x = arg_x;
// check if the point is valid
_check_validity();
}
void Point_2D::set_y(const double &arg_y)
{
m_y = arg_y;
// check if the point is valid
_check_validity();
}
void Point_2D::set(const double &arg_x, const double &arg_y)
{
m_x = arg_x;
m_y = arg_y;
// check if the point is valid
_check_validity();
}
// get the x coordinate and y coordinate
// accessable to const object
double Point_2D::get_x() const
{
return m_x;
}
double Point_2D::get_y() const
{
return m_y;
}
// Triangle_2D class implementation
// check & correct the Triangle_2D points to counterclockwise order
void Triangle_2D::_check_points()
{
// calculate the area of the Triangle_2D
double area = m_point[0].m_x * m_point[1].m_y +
m_point[1].m_x * m_point[2].m_y +
m_point[2].m_x * m_point[0].m_y -
m_point[0].m_x * m_point[2].m_y -
m_point[1].m_x * m_point[0].m_y -
m_point[2].m_x * m_point[1].m_y;
// if the area is negative, swap the points
if (area < 0.0)
{
Point_2D temp = m_point[0];
m_point[0] = m_point[1];
m_point[1] = temp;
}
}
// Constructor
Triangle_2D::Triangle_2D(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
: m_point{Point_2D(arg_x0, arg_y0),
Point_2D(arg_x1, arg_y1),
Point_2D(arg_x2, arg_y2)} // init the array with {}
{
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// Copy constructor
Triangle_2D::Triangle_2D(const Triangle_2D &arg_triangle)
: m_point{Point_2D(arg_triangle.m_point[0]),
Point_2D(arg_triangle.m_point[1]),
Point_2D(arg_triangle.m_point[2])} // init the array with {}
{
}
// print the Triangle_2D
void Triangle_2D::print()
{
// print the three points of the Triangle_2D
cout << "Triangle_2D: " << endl;
for (int i = 0; i < 3; i++)
{
m_point[i].print();
cout << endl;
}
}
// set the three points of the Triangle_2D
void Triangle_2D::set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
{
m_point[0].set(arg_x0, arg_y0);
m_point[1].set(arg_x1, arg_y1);
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point1(const double &arg_x0, const double &arg_y0)
{
m_point[0].set(arg_x0, arg_y0);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point2(const double &arg_x1, const double &arg_y1)
{
m_point[1].set(arg_x1, arg_y1);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point3(const double &arg_x2, const double &arg_y2)
{
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x0(const double &arg_x0)
{
m_point[0].m_x = arg_x0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y0(const double &arg_y0)
{
m_point[0].m_y = arg_y0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x1(const double &arg_x1)
{
m_point[1].m_x = arg_x1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y1(const double &arg_y1)
{
m_point[1].m_y = arg_y1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x2(const double &arg_x2)
{
m_point[2].m_x = arg_x2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y2(const double &arg_y2)
{
m_point[2].m_y = arg_y2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// get the three points of the Triangle_2D
double Triangle_2D::get_x0() const
{
return m_point[0].m_x;
}
double Triangle_2D::get_y0() const
{
return m_point[0].m_y;
}
double Triangle_2D::get_x1() const
{
return m_point[1].m_x;
}
double Triangle_2D::get_y1() const
{
return m_point[1].m_y;
}
double Triangle_2D::get_x2() const
{
return m_point[2].m_x;
}
double Triangle_2D::get_y2() const
{
return m_point[2].m_y;
}
// calculate the area of the Triangle_2D
double Triangle_2D::area()
{
// calculate the area of the Triangle_2D
return (m_point[0].m_x * m_point[1].m_y +
m_point[1].m_x * m_point[2].m_y +
m_point[2].m_x * m_point[0].m_y -
m_point[0].m_x * m_point[2].m_y -
m_point[1].m_x * m_point[0].m_y -
m_point[2].m_x * m_point[1].m_y) /
2.0;
}
// main function
int main()
{
Triangle_2D t(1, 1, 2, 2, 0, 3);
t.print();
cout << "Area: " << t.area() << endl;
// change the points of the Triangle_2D
t.set_points(1, 2, 2, 3, 3, 1);
t.print();
cout << "Area: " << t.area() << endl;
return 0;
}
Example 2: Vector
#include <iostream>
#include <cmath>
using namespace std;
class Vector_3D; // forward declaration
class Point_3D // represents a point in 3D space
{
private:
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// record the z coordinate
double m_z;
public:
Point_3D(const double &arg_x = 0, const double &arg_y = 0);
Point_3D(const Point_3D &arg_point);
// Destructor
~Point_3D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// print the x and y coordinate in format (x, y, z)
void print() const;
// modify the x, y and z coordinate
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
void set(const double &arg_x, const double &arg_y, const double &arg_z);
// get the x, y and z coordinate
double get_x() const;
double get_y() const;
double get_z() const;
// friend class
friend class Vector_3D;
};
// Vector_3D class declaration
class Vector_3D
{
private:
// define the three factor of the basis vectors
// on the x, y, z axes
double m_x, m_y, m_z;
public:
// Constructor
Vector_3D(const double &arg_x = 0.0, const double &arg_y = 0.0,
const double &arg_z = 0.0);
Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2);
// Copy constructor
Vector_3D(const Vector_3D &arg_vector);
// Destructor
~Vector_3D()
{
// do nothing
}
// print the Vector_3D
void print();
// set the three factor of the basis vectors
void set_vector(const double &arg_x, const double &arg_y,
const double &arg_z);
void set_vector(const Point_3D &arg_point1, const Point_3D &arg_point2);
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
// get the three factor of the basis vectors
double get_x() const;
double get_y() const;
double get_z() const;
// calculate the length of the Vector_3D
double length();
// calculate the dot product of two vectors
int dot(const Vector_3D &);
// calculate the cross product of two vectors
Vector_3D cross(const Vector_3D &);
};
// Vector_3D class implementation
// Constructor
Vector_3D::Vector_3D(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x), m_y(arg_y), m_z(arg_z)
{
}
Vector_3D::Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2)
: m_x(arg_point2.m_x - arg_point1.m_x),
m_y(arg_point2.m_y - arg_point1.m_y),
m_z(arg_point2.m_z - arg_point1.m_z)
{
}
// Copy constructor
Vector_3D::Vector_3D(const Vector_3D &arg_vector)
: m_x(arg_vector.m_x), m_y(arg_vector.m_y), m_z(arg_vector.m_z)
{
}
// print the Vector_3D
void Vector_3D::print()
{
// print the three factor of the basis vectors
cout << "Vector_3D: " << endl;
cout << "(" << m_x << ", " << m_y << ", " << m_z << ")" << endl;
}
// set the three factor of the basis vectors
void Vector_3D::set_vector(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
void Vector_3D::set_vector(const Point_3D &arg_point1,
const Point_3D &arg_point2)
{
m_x = arg_point2.m_x - arg_point1.m_x;
m_y = arg_point2.m_y - arg_point1.m_y;
m_z = arg_point2.m_z - arg_point1.m_z;
}
void Vector_3D::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Vector_3D::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Vector_3D::set_z(const double &arg_z)
{
m_z = arg_z;
}
// get the three factor of the basis vectors
double Vector_3D::get_x() const
{
return m_x;
}
double Vector_3D::get_y() const
{
return m_y;
}
double Vector_3D::get_z() const
{
return m_z;
}
// calculate the length of the Vector_3D
double Vector_3D::length()
{
// calculate the length of the Vector_3D
return sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
}
// calculate the dot product of two vectors
int Vector_3D::dot(const Vector_3D &arg_v)
{
// calculate the dot product of two vectors
return m_x * arg_v.m_x + m_y * arg_v.m_y + m_z * arg_v.m_z;
}
// calculate the cross product of two vectors
Vector_3D Vector_3D::cross(const Vector_3D &arg_v)
{
// calculate the cross product of two vectors
Vector_3D v;
v.m_x = m_y * arg_v.m_z - m_z * arg_v.m_y;
v.m_y = m_z * arg_v.m_x - m_x * arg_v.m_z;
v.m_z = m_x * arg_v.m_y - m_y * arg_v.m_x;
return v;
}
// main function
int main()
{
Vector_3D v1;
v1.print();
cout << endl;
cout << "Length of v1: " << v1.length() << endl;
v1.set_vector(1.0, 2.0, 3.0);
v1.print();
cout << endl;
cout << "Length of v1: " << v1.length() << endl;
cout << endl;
Vector_3D v2(v1);
v2.print();
cout << endl;
cout << "Length of v2: " << v2.length() << endl;
v2.set_vector(2.0, 3.0, 4.0);
v2.print();
cout << endl;
cout << "Length of v2: " << v2.length() << endl;
cout << endl;
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Dot: " << v1.dot(v2) << endl;
cout << endl;
v2.set_vector(1.0, 1.0, 1.0);
Vector_3D v3(v1.cross(v2));
cout << "v1: ";
v1.print();
cout << endl;
cout << "v2: ";
v2.print();
cout << endl;
cout << "Cross: ";
v3.print();
cout << endl;
cout << endl;
return 0;
}
Example 3: Fixed Point Number & Fixed Point Number Calculator
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
class Fp_Calc; // forward declaration
// Fixed point class declaration
class Fixed_Point
{
private:
long long int m_int_part;
long long int m_frac_part;
unsigned int m_precision;
// utility functions
// set fixed point without checking
void _set(const string &arg_str);
// normalize to m_precision
void _normalize(const unsigned int arg_precision = 0);
public:
Fixed_Point(const long long int &arg_int_part = 0,
const unsigned long long int &arg_frac_part = 0,
const unsigned int &arg_precision = 9);
Fixed_Point(const string &arg_str);
~Fixed_Point();
// getter & setter
void set_int_part(const long long int arg_int_part);
void set_frac_part(const unsigned long long int arg_frac_part);
void set_precision(const unsigned int arg_precision);
void set(const long long int &arg_int_part,
const unsigned long long int &arg_frac_part,
const unsigned int &arg_precision);
void set(const string &arg_str);
void set(const double &arg_double);
void set(const float &arg_float);
long long int get_int_part() const;
unsigned long long int get_frac_part() const;
unsigned int get_precision() const;
double get_double_value() const;
float get_float_value() const;
string get_string_value() const;
// formatted output
void print() const;
// arithmetic operation
Fixed_Point add(const Fixed_Point &arg_fp) const;
Fixed_Point sub(const Fixed_Point &arg_fp) const;
// friend class
friend class Fp_Calc;
};
// Fixed point calculator class declaration
class Fp_Calc
{
private:
// define current value
Fixed_Point m_curr_val;
// define input value
Fixed_Point m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and ` ` for none
char m_op;
// calculate result
void _calc_result();
public:
// Constructor
Fp_Calc();
// Copy constructor
Fp_Calc(const Fp_Calc &arg_int_calc);
// Destructor
~Fp_Calc(){}; // no need to do anything
// clear the input value
void clear();
// set the input value
void set_input(const string &arg_input);
// add the input value to the current value
void add();
// subtract the input value from the current value
void sub();
// multiply the input value with the current value
void mul();
// divide the current value by the input value
void div();
// assign the input value to the current value
void assign();
// get the current value
Fixed_Point get_curr_val();
// get the current operation
char get_op();
// get the input value
Fixed_Point get_input_val();
};
// Fixed point class implementation
// utility functions
// set fixed point without checking
void Fixed_Point::_set(const string &arg_str)
{
// set integer part
m_int_part = stoll(arg_str.substr(0, arg_str.find('.')));
// set fractional part
m_frac_part = stoull(arg_str.substr(arg_str.find('.') + 1));
// set precision
m_precision = arg_str.length() - arg_str.find('.') - 1;
}
// normalize to precision
void Fixed_Point::_normalize(const unsigned int arg_precision)
{
unsigned int temp_precision = arg_precision;
// if precision is not specified, use the current precision
if (arg_precision == 0)
{
temp_precision = m_precision;
}
// if precision is over the maximum, use the maximum
else if (arg_precision > 9)
{
temp_precision = 9;
}
else
{
temp_precision = arg_precision;
}
// update fractional part
int precision_diff = temp_precision - m_precision;
if (precision_diff > 0)
{
m_frac_part *= pow(10, precision_diff);
}
else if (precision_diff < 0)
{
m_frac_part /= pow(10, -precision_diff);
}
// update m_precision
m_precision = temp_precision;
// handle fractional part overflow
// update integer part
if (m_frac_part >= pow(10, m_precision))
{
m_int_part += m_frac_part / pow(10, m_precision);
m_frac_part %= (int)pow(10, m_precision);
}
// handle fractional part underflow
// update integer part
if (m_frac_part < 0)
{
m_int_part -= 1;
m_frac_part += pow(10, m_precision);
}
}
// Constructor
Fixed_Point::Fixed_Point(const long long int &arg_int_part,
const unsigned long long int &arg_frac_part,
const unsigned int &arg_precision)
: m_int_part(arg_int_part),
m_frac_part(arg_frac_part),
m_precision(arg_precision)
{
}
Fixed_Point::Fixed_Point(const string &arg_string)
{
_set(arg_string);
_normalize();
}
Fixed_Point::~Fixed_Point()
{
// do nothing
}
// getter & setter
void Fixed_Point::set_int_part(const long long int arg_int_part)
{
m_int_part = arg_int_part;
}
void Fixed_Point::set_frac_part(const unsigned long long int arg_frac_part)
{
m_frac_part = arg_frac_part;
_normalize();
}
void Fixed_Point::set_precision(const unsigned int arg_precision)
{
_normalize(arg_precision);
}
void Fixed_Point::set(const long long int &arg_int_part,
const unsigned long long int &arg_frac_part,
const unsigned int &arg_precision)
{
m_int_part = arg_int_part;
m_frac_part = arg_frac_part;
m_precision = arg_precision;
_normalize();
}
void Fixed_Point::set(const string &arg_str)
{
_set(arg_str);
_normalize();
}
void Fixed_Point::set(const double &arg_double)
{
_set(to_string(arg_double));
_normalize();
}
void Fixed_Point::set(const float &arg_float)
{
_set(to_string(arg_float));
_normalize();
}
long long int Fixed_Point::get_int_part() const
{
return m_int_part;
}
unsigned long long int Fixed_Point::get_frac_part() const
{
return m_frac_part;
}
unsigned int Fixed_Point::get_precision() const
{
return m_precision;
}
double Fixed_Point::get_double_value() const
{
return double(m_int_part) + double(m_frac_part) / pow(10, m_precision);
}
float Fixed_Point::get_float_value() const
{
return float(m_int_part) + float(m_frac_part) / pow(10, m_precision);
}
string Fixed_Point::get_string_value() const
{
string str_int_part = to_string(m_int_part);
string str_frac_part = to_string(m_frac_part);
// if precision is not specified, use the current precision
if (m_precision == 0)
{
return str_int_part;
}
// if precision is 1, return integer part and fractional part
else if (m_precision == 1)
{
return str_int_part + "." + str_frac_part;
}
// if precision is over 1, return integer part and fractional part with
// specified precision
else
{
// if fractional part is 0, return integer part
if (str_frac_part == "0")
{
return str_int_part;
}
// if fractional part is not 0, return integer part and fractional part
else
{
// if fractional part is less than precision, add 0 to the front
if (str_frac_part.length() < m_precision)
{
str_frac_part = string(m_precision - str_frac_part.length(), '0') + str_frac_part;
}
// if fractional part is more than precision, remove the end
else if (str_frac_part.length() > m_precision)
{
str_frac_part = str_frac_part.substr(0, m_precision);
}
return str_int_part + "." + str_frac_part;
}
}
}
void Fixed_Point::print() const
{
cout << get_string_value();
}
Fixed_Point Fixed_Point::add(const Fixed_Point &arg_fixed_point) const
{
Fixed_Point result;
Fixed_Point normalized_this(*this);
Fixed_Point normalized_arg(arg_fixed_point);
unsigned int max_precision = max(normalized_this.m_precision,
normalized_arg.m_precision);
normalized_this.set_precision(max_precision);
normalized_arg.set_precision(max_precision);
result.m_precision = max_precision;
result.m_int_part = normalized_this.m_int_part + normalized_arg.m_int_part;
result.m_frac_part = normalized_this.m_frac_part + normalized_arg.m_frac_part;
result._normalize();
return result;
}
Fixed_Point Fixed_Point::sub(const Fixed_Point &arg_fixed_point) const
{
Fixed_Point result;
Fixed_Point normalized_this(*this);
Fixed_Point normalized_arg(arg_fixed_point);
unsigned int max_precision = max(normalized_this.m_precision,
normalized_arg.m_precision);
normalized_this.set_precision(max_precision);
normalized_arg.set_precision(max_precision);
result.m_precision = max_precision;
result.m_int_part = normalized_this.m_int_part - normalized_arg.m_int_part;
result.m_frac_part = normalized_this.m_frac_part - normalized_arg.m_frac_part;
result._normalize();
return result;
}
// Fp_Calc class implementation
// Constructor
Fp_Calc::Fp_Calc()
: m_curr_val(), m_input_val(), m_op(' ')
{
}
// Copy constructor
Fp_Calc::Fp_Calc(const Fp_Calc &arg_int_calc)
: m_curr_val(arg_int_calc.m_curr_val),
m_input_val(arg_int_calc.m_input_val),
m_op(arg_int_calc.m_op)
{
}
// calculate the result
void Fp_Calc::_calc_result()
{
switch (m_op)
{
case '+':
m_curr_val = m_curr_val.add(m_input_val);
break;
case '-':
m_curr_val = m_curr_val.sub(m_input_val);
break;
case ' ':
m_curr_val = m_input_val;
break;
default:
break;
}
}
// clear the input value
void Fp_Calc::clear()
{
m_input_val = Fixed_Point();
}
// set the input value
void Fp_Calc::set_input(const string &arg_input_val)
{
m_input_val = Fixed_Point(arg_input_val);
}
// add the input value to the current value
void Fp_Calc::add()
{
_calc_result();
m_op = '+';
}
// subtract the input value from the current value
void Fp_Calc::sub()
{
_calc_result();
m_op = '-';
}
// multiply the input value with the current value
void Fp_Calc::mul()
{
_calc_result();
m_op = '*';
}
// divide the current value by the input value
void Fp_Calc::div()
{
_calc_result();
m_op = '/';
}
// assign the input value to the current value
void Fp_Calc::assign()
{
_calc_result();
m_op = ' ';
}
// get the current value
Fixed_Point Fp_Calc::get_curr_val()
{
return m_curr_val;
}
// get the current operation
char Fp_Calc::get_op()
{
return m_op;
}
// get the input value
Fixed_Point Fp_Calc::get_input_val()
{
return m_input_val;
}
// main function
int main()
{
// create an instance of the class
Fp_Calc calc;
// set the input value
calc.set_input("10.0");
// get the input value
calc.get_input_val().print();
cout << endl;
// add the input value to the current value
calc.add();
// get current op
cout << '\'' << calc.get_op() << '\'' << endl;
// set another input value
calc.set_input("20.0123");
// get the input value
calc.get_input_val().print();
cout << endl;
// clear the input value
calc.clear();
cout << "clear" << endl;
// set the input value
calc.set_input("30.000456");
// get the input value
calc.get_input_val().print();
cout << endl;
// subtract the input value from the current value
calc.sub();
// get current op
cout << '\'' << calc.get_op() << '\'' << endl;
// print the result
calc.get_curr_val().print();
cout << endl;
// set another input value
calc.set_input("20.0123");
// get the input value
calc.get_input_val().print();
cout << endl;
// compute the result
calc.assign();
// print the result
calc.get_curr_val().print();
cout << endl;
}
Operator & Operator Overloading
Slides version: lecture6_slides.html Website version: lecture6.html
- What is Operator?
- How to write/use your own operator? (Operator Overloading)
- Syntax
- Unary, Binary, Ternary
- Example
- Syntax
- Overloading other class's/global operator
- Example: cout
<<& cin>>operator
- Example: cout
- How to design your own operator?
- Guidelines
- Example
- Example: Triangle (again)
- Example: Vector (again)
- Example: Fixed Point Number & Fixed Point Number Calculator (again)
- Lab 6: Complex Number Calculator
What is Operator?
Ref: C++ Operator Precedence - cppreference.com
| precedence (partial) | operator |
|---|---|
| 1 | a++, a-- |
| 2 | ++a, --a |
| 3 | +a, -a |
!a, ~a | |
(type) | |
| 5 | a * b, a / b, a % b |
| 6 | a + b, a - b |
| 7 | a << b, a >> b |
| 9 | a < b, a <= b, a > b, a >= b |
| 10 | a == b, a != b |
| 11 | a & b |
| 12 | a ^ b |
| 13 | a \| b |
| 14 | a && b |
| 15 | a \|\| b |
| 16 | a ? b : c, a = b, a += b, a -= b, a *= b, a /= b |
a %= b, a <<= b, a >>= b, a &= b, a ^= b, a \|= b |
How to write/use your own operator? (Operator Overloading)
Example: Point_2D (partial)
- we want to compare two
Point_2D - we want to assign a
Point_2Dto anotherPoint_2D - we want to print/output a
Point_2D - we want to read/input a
Point_2D
naive implementation:
class Point_2D
{
private:
/// ...
public:
/// ...
// print the point in the format (x, y)
void print() const;
// read the point from input
void read();
// modify the x and y coordinate
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set(const double &arg_x, const double &arg_y);
// get the x coordinate and y coordinate
double get_x() const;
double get_y() const;
// compare two points
bool equal(const Point_2D &arg_point) const;
bool not_equal(const Point_2D &arg_point) const;
bool less(const Point_2D &arg_point) const;
bool greater(const Point_2D &arg_point) const;
bool less_equal(const Point_2D &arg_point) const;
bool greater_equal(const Point_2D &arg_point) const;
// assign the point with another point
Point_2D assign(const Point_2D &arg_point);
};
Can we use operator like >, != to implement the above? Yes!
class Point_2D
{
private:
/// ...
public:
/// ...
// print the point in the format (x, y)
friend std::ostream &operator<<(std::ostream &os, const Point_2D &arg_point);
// read the point from input
friend std::istream &operator>>(std::istream &is, Point_2D &arg_point);
// modify the x and y coordinate
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set(const double &arg_x, const double &arg_y);
// get the x coordinate and y coordinate
double get_x() const;
double get_y() const;
// compare two points
bool operator==(const Point_2D &arg_point) const;
bool operator!=(const Point_2D &arg_point) const;
bool operator<(const Point_2D &arg_point) const;
bool operator>(const Point_2D &arg_point) const;
bool operator<=(const Point_2D &arg_point) const;
bool operator>=(const Point_2D &arg_point) const;
// assign the point with another point
Point_2D operator=(const Point_2D &arg_point);
};
Usage:
int main()
{
Point_2D point1, point2;
cin >> point1 >> point2;
cout << point1 << point2 << endl;
if (point1 == point2)
{
std::cout << "point1 == point2" << std::endl;
}
else
{
std::cout << "point1 != point2" << std::endl;
}
point1 = point2;
if (point1 == point2)
{
std::cout << "point1 == point2" << std::endl;
}
else
{
std::cout << "point1 != point2" << std::endl;
}
return 0;
}
Syntax
Ref: Operator Overloading in C++ - GeeksforGeeks, operator overloading - cppreference.com
operator<op>, where<op>is one of the following:+,-,*,/,%,^,&,|,~,!,=,<,>,+=,-=,*=,/=,%=,^=,&=,|=,<<,>>,>>=,<<=,==,!=,<=,>=,&&,||,++,--,,,->*,->,( ),[ ]
operator <type>, where<type>is one of the following: (type conversion)int,long,long long,unsigned,unsigned long,unsigned long long,float,double,long double,char,bool, or user-defined type defined bytypedef
Syntax (cont.)
- 2 types of operator:
- unary operator:
(a).operator@(),operator@(),(a).operator@(0),operator@(a, 0) - binary operator:
(a).operator@(b),operator@(a, b),(a).operator=(b)
- unary operator:
Example (member function)
#include <iostream>
using namespace std;
class Complex
{
private:
int real, imag;
public:
Complex(int r = 0, int i = 0)
{
real = r;
imag = i;
}
// This is automatically called when '+' is used with
// between two Complex objects
Complex operator+(Complex const &obj)
{
Complex res;
res.real = real + obj.real;
res.imag = imag + obj.imag;
return res;
}
void print() { cout << real << " + i" << imag << '\n'; }
};
int main()
{
Complex c1(10, 5), c2(2, 4);
Complex c3 = c1 + c2;
c3.print();
}
Example (friend function)
#include <iostream>
using namespace std;
class Complex
{
private:
int real, imag;
public:
Complex(int r = 0, int i = 0)
{
real = r;
imag = i;
}
void print() { cout << real << " + i" << imag << '\n'; }
// The global operator function is made friend of this class so
// that it can access private members
friend Complex operator+(Complex const &, Complex const &);
};
Complex operator+(Complex const &c1, Complex const &c2)
{
return Complex(c1.real + c2.real, c1.imag + c2.imag);
}
int main()
{
Complex c1(10, 5), c2(2, 4);
Complex c3 = c1 + c2;
c3.print();
return 0;
}
Example (type conversion)
#include <iostream>
using namespace std;
class Fraction
{
private:
int num, den;
public:
Fraction(int n, int d) { num = n; den = d; }
// Conversion operator: return float value of fraction
operator float() const {
return float(num) / float(den);
}
};
int main() {
Fraction f(2, 5);
float val = f;
cout << val << '\n';
return 0;
}
Overloading other class's/global operator
Ref: operator overloading - cppreference.com
- Global operator: To overload a global operator, you can define a function with the same name as the operator.
- Other class's operator: To overload a member operator, you need to inherit from the class and define a function with the same name as the operator. (disscuss in Lecture 9)
Example: cout << & cin >> operator
#include <iostream>
#include <string>
using namespace std;
class Point_2D
{
private:
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
public:
// print the point in the format (x, y)
friend std::ostream &operator<<(std::ostream &arg_os, const Point_2D &arg_point)
{
arg_os << "(" << arg_point.m_x << ", " << arg_point.m_y << ")";
return arg_os;
}
// read the coordinate of a point from the input, format: (x, y) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Point_2D &arg_point)
{
string str_x, str_y, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ')'))
{
arg_point.m_x = stod(str_x);
arg_point.m_y = stod(str_y);
}
}
}
return arg_is;
}
};
int main()
{
Point_2D point;
cin >> point;
cout << point << endl;
return 0;
}
Output:
$ ./a.out
(1.0, 2.0)⏎
(1, 2)
$
How to design your own operator?
Ref: Google C++ Style Guide, This section is licensed under the Apache License 2.0
Define overloaded operators only if their meaning is obvious, unsurprising, and consistent with the corresponding built-in operators. For example, use
|as a bitwise- or logical-or, not as a shell-style pipe.
Define operators only on your own types. More precisely, define them in the same headers, .cc files, and namespaces as the types they operate on. That way, the operators are available wherever the type is, minimizing the risk of multiple definitions. If possible, avoid defining operators as templates, because they must satisfy this rule for any possible template arguments. If you define an operator, also define any related operators that make sense, and make sure they are defined consistently. For example, if you overload
<, overload all the comparison operators, and make sure<and>never return true for the same arguments.
Prefer to define non-modifying binary operators as non-member functions. If a binary operator is defined as a class member, implicit conversions will apply to the right-hand argument, but not the left-hand one. It will confuse your users if
a < bcompiles butb < adoesn't.
Don't go out of your way to avoid defining operator overloads. For example, prefer to define
==,=, and<<, rather thanEquals(),CopyFrom(), andPrintTo(). Conversely, don't define operator overloads just because other libraries expect them. For example, if your type doesn't have a natural ordering, but you want to store it in astd::set, use a custom comparator rather than overloading<.
Do not overload
&&,||,,(comma), or unary&. Do not overloadoperator"", i.e., do not introduce user-defined literals. Do not use any such literals provided by others (including the standard library).
Type conversion operators are covered in the section on implicit conversions. The
=operator is covered in the section on copy constructors. Overloading<<for use with streams is covered in the section on streams. See also the rules on function overloading, which apply to operator overloading as well.
Example 1: Triangle (again) [Source]
A Triangle:
- contains 3 points
- on the 2D plane
- need to be able to calculate the area
- need to be initialized, printed, and modified
Example 2: Vector (again) [Source]
A Vector:
- contains 3 factors of the 3 basis $\bold{i}$, $\bold{j}$, $\bold{k}$
- need to be able to calculate the length
- need to be able to calculate the dot, cross product
- need to be initialized, printed, and modified
Example 3: Fixed Point Number & Fixed Point Number Calculator (again) [Source]
A Fixed Point Number:
- contains a integer part, a fractional part, and a precision
- need to be able to calculate the sum, difference
- need to be able to convert to/from string,
float, anddouble - need to be initialized, printed, and modified
A Fixed Point Number Calculator:
- contains current value, input value, and operation
- need to be able to set the input value
- need to be able to set the operation
- need to be able to calculate the result
- need to be able to clear the input value
- need to be initialized
- need to be able to get all information
Lab 6: Complex Number Calculator
Example 1: Trangle
#include <iostream>
using namespace std;
class Triangle_2D; // forward declaration
class Point_2D // the class name
// we use first upper case letter to indicate a class
{
private: // private data members & member functions
// Data members
// we use `m_` to indicate a data member
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// Member functions
// we use `_` to indicate a member function
// check if the point is valid
void _check_validity();
public: // public member functions
// Constructor
// Constructor & Default constructor
// initialize data members, with default values
// accessable to const object by default
Point_2D(const double &arg_x = 0, const double &arg_y = 0);
// Copy constructor
// copy the data members from the given object
// accessable to const object by default
Point_2D(const Point_2D &arg_point);
// Destructor
~Point_2D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// Member functions
// we use lower case letter to indicate a member function
// also, we just define the function declaration
// and leave the definition to the end of the class
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set(const double &arg_x, const double &arg_y);
// get the x coordinate and y coordinate
// accessable to const object
double get_x() const;
double get_y() const;
// // compare two points
bool operator==(const Point_2D &arg_point) const;
bool operator!=(const Point_2D &arg_point) const;
bool operator<(const Point_2D &arg_point) const;
bool operator>(const Point_2D &arg_point) const;
bool operator<=(const Point_2D &arg_point) const;
bool operator>=(const Point_2D &arg_point) const;
// assign the point with another point
Point_2D &operator=(const Point_2D &arg_point);
// friend class
friend class Triangle_2D;
// friend function
// print the x and y coordinate in format (x, y)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os, const Point_2D &arg_point);
// read the coordinate of a point from the input, format: (x, y) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Point_2D &arg_point);
};
// Triangle_2D class declaration
class Triangle_2D
{
private:
// define three points of the Triangle_2D
// in array of Point_2D format
Point_2D m_point[3];
// check & correct the Triangle_2D points to counterclockwise order
void _check_points();
public:
// Constructor
Triangle_2D(const double &arg_x0 = 0.0, const double &arg_y0 = 0.0,
const double &arg_x1 = 0.0, const double &arg_y1 = 0.0,
const double &arg_x2 = 0.0, const double &arg_y2 = 0.0);
// Copy constructor
Triangle_2D(const Triangle_2D &arg_triangle);
// Destructor
~Triangle_2D()
{
// do nothing
}
// modify the three points of the Triangle_2D
void set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2);
void set_point1(const double &arg_x0, const double &arg_y0);
void set_point2(const double &arg_x1, const double &arg_y1);
void set_point3(const double &arg_x2, const double &arg_y2);
void set_x0(const double &arg_x0);
void set_y0(const double &arg_y0);
void set_x1(const double &arg_x1);
void set_y1(const double &arg_y1);
void set_x2(const double &arg_x2);
void set_y2(const double &arg_y2);
// get the three points of the Triangle_2D
double get_x0() const;
double get_y0() const;
double get_x1() const;
double get_y1() const;
double get_x2() const;
double get_y2() const;
// calculate the area of the Triangle_2D
double area();
// print the Triangle_2D
// format: ((x0, y0), (x1, y1), (x2, y2))
friend std::ostream &operator<<(std::ostream &arg_os, const Triangle_2D &arg_tri);
// read the coordinate of a point from the input,
// format: ((x0, y0), (x1, y1), (x2, y2)) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Triangle_2D &arg_tri);
};
// function definition
// check if the point is valid
void Point_2D::_check_validity()
{
// check if the x coordinate is valid
if (m_x < 0)
{
// if not, set it to 0
m_x = 0;
}
// check if the y coordinate is valid
if (m_y < 0)
{
// if not, set it to 0
m_y = 0;
}
}
// Constructor & Default constructor
// initialize data members, with default values
Point_2D::Point_2D(const double &arg_x, const double &arg_y)
// use `: var_name1(arg_var_name1), var_name2(arg_var_name2)`
// to initialize data members
: m_x(arg_x),
m_y(arg_y)
{
// check if the point is valid
_check_validity();
}
// Copy constructor
// copy the data members from the given object
Point_2D::Point_2D(const Point_2D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y)
{
// check if the point is valid
_check_validity();
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_2D::set_x(const double &arg_x)
{
m_x = arg_x;
// check if the point is valid
_check_validity();
}
void Point_2D::set_y(const double &arg_y)
{
m_y = arg_y;
// check if the point is valid
_check_validity();
}
void Point_2D::set(const double &arg_x, const double &arg_y)
{
m_x = arg_x;
m_y = arg_y;
// check if the point is valid
_check_validity();
}
// get the x coordinate and y coordinate
// accessable to const object
double Point_2D::get_x() const
{
return m_x;
}
double Point_2D::get_y() const
{
return m_y;
}
// // compare two points
bool Point_2D::operator==(const Point_2D &arg_point) const
{
// if the x and y coordinates are equal,
// return true
return (m_x == arg_point.m_x && m_y == arg_point.m_y);
}
bool Point_2D::operator!=(const Point_2D &arg_point) const
{
return !(*this == arg_point);
}
bool Point_2D::operator<(const Point_2D &arg_point) const
{
// if the x coordinate is smaller than the other point,
// return true
if (m_x < arg_point.m_x)
{
return true;
}
// if the x coordinate is equal to the other point,
// check if the y coordinate is smaller than the other point
else if (m_x == arg_point.m_x)
{
// if the y coordinate is smaller, return true
if (m_y < arg_point.m_y)
{
return true;
}
// if the y coordinate is equal to the other point,
// return false
else if (m_y == arg_point.m_y)
{
return false;
}
// if the y coordinate is larger, return false
else
{
return false;
}
}
// if the x coordinate is larger, return false
else
{
return false;
}
}
bool Point_2D::operator>(const Point_2D &arg_point) const
{
return !(*this < arg_point || *this == arg_point);
}
bool Point_2D::operator<=(const Point_2D &arg_point) const
{
return (*this < arg_point || *this == arg_point);
}
bool Point_2D::operator>=(const Point_2D &arg_point) const
{
return !(*this < arg_point);
}
// assign the point with another point
Point_2D &Point_2D::operator=(const Point_2D &arg_point)
{
// check if the point is valid
_check_validity();
// assign the x and y coordinate
m_x = arg_point.m_x;
m_y = arg_point.m_y;
// check if the point is valid
_check_validity();
return *this;
}
// print the point in the format (x, y)
std::ostream &operator<<(std::ostream &arg_os, const Point_2D &arg_point)
{
arg_os << "(" << arg_point.m_x << ", " << arg_point.m_y << ")";
return arg_os;
}
// read the coordinate of a point from the input, format: (x, y) and ignore space
std::istream &operator>>(std::istream &arg_is, Point_2D &arg_point)
{
string str_x, str_y, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ')'))
{
arg_point.m_x = stod(str_x);
arg_point.m_y = stod(str_y);
}
}
}
// check if the point is valid
arg_point._check_validity();
return arg_is;
}
// Triangle_2D class implementation
// check & correct the Triangle_2D points to counterclockwise order
void Triangle_2D::_check_points()
{
// sort the points in ascending order
for (int i = 0; i < 3; i++)
{
for (int j = i + 1; j < 3; j++)
{
if (m_point[i] > m_point[j])
{
// swap the points
Point_2D temp = m_point[i];
m_point[i] = m_point[j];
m_point[j] = temp;
}
}
}
// if the area is negative, swap the points
if (area() < 0.0)
{
Point_2D temp = m_point[0];
m_point[0] = m_point[1];
m_point[1] = temp;
}
}
// Constructor
Triangle_2D::Triangle_2D(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
: m_point{Point_2D(arg_x0, arg_y0),
Point_2D(arg_x1, arg_y1),
Point_2D(arg_x2, arg_y2)} // init the array with {}
{
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// Copy constructor
Triangle_2D::Triangle_2D(const Triangle_2D &arg_triangle)
: m_point{Point_2D(arg_triangle.m_point[0]),
Point_2D(arg_triangle.m_point[1]),
Point_2D(arg_triangle.m_point[2])} // init the array with {}
{
}
// set the three points of the Triangle_2D
void Triangle_2D::set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
{
m_point[0].set(arg_x0, arg_y0);
m_point[1].set(arg_x1, arg_y1);
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point1(const double &arg_x0, const double &arg_y0)
{
m_point[0].set(arg_x0, arg_y0);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point2(const double &arg_x1, const double &arg_y1)
{
m_point[1].set(arg_x1, arg_y1);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point3(const double &arg_x2, const double &arg_y2)
{
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x0(const double &arg_x0)
{
m_point[0].m_x = arg_x0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y0(const double &arg_y0)
{
m_point[0].m_y = arg_y0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x1(const double &arg_x1)
{
m_point[1].m_x = arg_x1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y1(const double &arg_y1)
{
m_point[1].m_y = arg_y1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x2(const double &arg_x2)
{
m_point[2].m_x = arg_x2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y2(const double &arg_y2)
{
m_point[2].m_y = arg_y2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// get the three points of the Triangle_2D
double Triangle_2D::get_x0() const
{
return m_point[0].m_x;
}
double Triangle_2D::get_y0() const
{
return m_point[0].m_y;
}
double Triangle_2D::get_x1() const
{
return m_point[1].m_x;
}
double Triangle_2D::get_y1() const
{
return m_point[1].m_y;
}
double Triangle_2D::get_x2() const
{
return m_point[2].m_x;
}
double Triangle_2D::get_y2() const
{
return m_point[2].m_y;
}
// calculate the area of the Triangle_2D
double Triangle_2D::area()
{
// calculate the area of the Triangle_2D
return (m_point[0].m_x * m_point[1].m_y +
m_point[1].m_x * m_point[2].m_y +
m_point[2].m_x * m_point[0].m_y -
m_point[0].m_x * m_point[2].m_y -
m_point[1].m_x * m_point[0].m_y -
m_point[2].m_x * m_point[1].m_y) /
2.0;
}
// print the Triangle_2D
// format: ((x0, y0), (x1, y1), (x2, y2))
std::ostream &operator<<(std::ostream &arg_os, const Triangle_2D &arg_tri)
{
arg_os << "(";
for (int i = 0; i < 3; i++)
{
arg_os << arg_tri.m_point[i];
if (i < 2)
arg_os << ", ";
}
arg_os << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: ((x0, y0), (x1, y1), (x2, y2)) and ignore space
std::istream &operator>>(std::istream &arg_is, Triangle_2D &arg_tri)
{
string temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
for (int i = 0; i < 3; i++)
{
arg_is >> arg_tri.m_point[i];
if (i < 2)
{
getline(arg_is, temp, ','); // ignore the ','
}
}
getline(arg_is, temp, ')'); // ignore the last ')'
}
// check & correct the Triangle_2D points to counterclockwise order
arg_tri._check_points();
return arg_is;
}
// main function
int main()
{
Triangle_2D t(1, 1, 2, 2, 0, 3);
cout << t << endl;
cout << "Area: " << t.area() << endl;
// change the points of the Triangle_2D
cin >> t;
cout << t << endl;
cout << "Area: " << t.area() << endl;
return 0;
}
Example 2: Vector
#include <iostream>
#include <cmath>
using namespace std;
class Vector_3D; // forward declaration
class Point_3D // represents a point in 3D space
{
private:
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// record the z coordinate
double m_z;
public:
Point_3D(const double &arg_x = 0, const double &arg_y = 0,
const double &arg_z = 0);
Point_3D(const Point_3D &arg_point);
// Destructor
~Point_3D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// modify the x, y and z coordinate
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
void set(const double &arg_x, const double &arg_y, const double &arg_z);
// get the x, y and z coordinate
double get_x() const;
double get_y() const;
double get_z() const;
// calculate the distance between two points
// in form of a vector
Vector_3D operator-(const Point_3D &arg_point) const;
// friend class
friend class Vector_3D;
// print the x and y coordinate in format (x, y, z)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os, const Point_3D &arg_point);
// read the coordinate of a point from the input,
// format: (x, y, z) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Point_3D &arg_point);
};
// Vector_3D class declaration
class Vector_3D
{
private:
// define the three factor of the basis vectors
// on the x, y, z axes
double m_x, m_y, m_z;
public:
// Constructor
Vector_3D(const double &arg_x = 0.0, const double &arg_y = 0.0,
const double &arg_z = 0.0);
Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2);
// Copy constructor
Vector_3D(const Vector_3D &arg_vector);
// Destructor
~Vector_3D()
{
// do nothing
}
// set the three factor of the basis vectors
void set_vector(const double &arg_x, const double &arg_y,
const double &arg_z);
void set_vector(const Point_3D &arg_point1, const Point_3D &arg_point2);
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
// get the three factor of the basis vectors
double get_x() const;
double get_y() const;
double get_z() const;
// assign operator
Vector_3D &operator=(const Vector_3D &arg_vector);
// calculate the length of the Vector_3D
double length();
// calculate the dot product of two vectors
int dot(const Vector_3D &);
// calculate the cross product of two vectors
Vector_3D cross(const Vector_3D &);
// print the Vector_3D in format (x, y, z)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os,
const Vector_3D &arg_point);
// read the factors of a vector from the input,
// format: (x, y, z) and ignore space
friend std::istream &operator>>(std::istream &arg_is,
Vector_3D &arg_point);
};
// Point_3D class implementation
// Constructor & Default constructor
// initialize data members, with default values
Point_3D::Point_3D(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x),
m_y(arg_y),
m_z(arg_z)
{
}
// Copy constructor
// copy the data members from the given object
Point_3D::Point_3D(const Point_3D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y),
m_z(arg_point.m_z)
{
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_3D::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Point_3D::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Point_3D::set(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
// get the x coordinate and y coordinate
// accessable to const object
double Point_3D::get_x() const
{
return m_x;
}
double Point_3D::get_y() const
{
return m_y;
}
double Point_3D::get_z() const
{
return m_z;
}
// calculate the distance between two points
// in form of a vector
Vector_3D Point_3D::operator-(const Point_3D &arg_point) const
{
return Vector_3D(*this, arg_point);
}
// print the point in the format (x, y, z)
std::ostream &operator<<(std::ostream &arg_os, const Point_3D &arg_point)
{
arg_os << "(" << arg_point.m_x << ", " << arg_point.m_y
<< ", " << arg_point.m_z << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: (x, y, z) and ignore space
std::istream &operator>>(std::istream &arg_is, Point_3D &arg_point)
{
string str_x, str_y, str_z, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ','))
{
if (getline(arg_is, str_z, ')'))
{
arg_point.m_x = stod(str_x);
arg_point.m_y = stod(str_y);
arg_point.m_z = stod(str_z);
}
}
}
}
return arg_is;
}
// Vector_3D class implementation
// Constructor
Vector_3D::Vector_3D(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x), m_y(arg_y), m_z(arg_z)
{
}
Vector_3D::Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2)
: m_x(arg_point2.m_x - arg_point1.m_x),
m_y(arg_point2.m_y - arg_point1.m_y),
m_z(arg_point2.m_z - arg_point1.m_z)
{
}
// Copy constructor
Vector_3D::Vector_3D(const Vector_3D &arg_vector)
: m_x(arg_vector.m_x), m_y(arg_vector.m_y), m_z(arg_vector.m_z)
{
}
// set the three factor of the basis vectors
void Vector_3D::set_vector(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
void Vector_3D::set_vector(const Point_3D &arg_point1,
const Point_3D &arg_point2)
{
m_x = arg_point2.m_x - arg_point1.m_x;
m_y = arg_point2.m_y - arg_point1.m_y;
m_z = arg_point2.m_z - arg_point1.m_z;
}
void Vector_3D::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Vector_3D::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Vector_3D::set_z(const double &arg_z)
{
m_z = arg_z;
}
// get the three factor of the basis vectors
double Vector_3D::get_x() const
{
return m_x;
}
double Vector_3D::get_y() const
{
return m_y;
}
double Vector_3D::get_z() const
{
return m_z;
}
// assign operator
Vector_3D &Vector_3D::operator=(const Vector_3D &arg_vector)
{
m_x = arg_vector.m_x;
m_y = arg_vector.m_y;
m_z = arg_vector.m_z;
return *this;
}
// calculate the length of the Vector_3D
double Vector_3D::length()
{
// calculate the length of the Vector_3D
return sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
}
// calculate the dot product of two vectors
int Vector_3D::dot(const Vector_3D &arg_v)
{
// calculate the dot product of two vectors
return m_x * arg_v.m_x + m_y * arg_v.m_y + m_z * arg_v.m_z;
}
// calculate the cross product of two vectors
Vector_3D Vector_3D::cross(const Vector_3D &arg_v)
{
// calculate the cross product of two vectors
Vector_3D v;
v.m_x = m_y * arg_v.m_z - m_z * arg_v.m_y;
v.m_y = m_z * arg_v.m_x - m_x * arg_v.m_z;
v.m_z = m_x * arg_v.m_y - m_y * arg_v.m_x;
return v;
}
// print the point in the format (x, y, z)
std::ostream &operator<<(std::ostream &arg_os, const Vector_3D &arg_vector)
{
arg_os << "(" << arg_vector.m_x << ", " << arg_vector.m_y
<< ", " << arg_vector.m_z << ")";
return arg_os;
}
// read the factors of a vector from the input,
// format: (x, y, z) and ignore space
std::istream &operator>>(std::istream &arg_is, Vector_3D &arg_vector)
{
string str_x, str_y, str_z, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ','))
{
if (getline(arg_is, str_z, ')'))
{
arg_vector.m_x = stod(str_x);
arg_vector.m_y = stod(str_y);
arg_vector.m_z = stod(str_z);
}
}
}
}
return arg_is;
}
// main function
int main()
{
Vector_3D v1;
cout << v1 << endl;
cout << "Length of v1: " << v1.length() << endl;
cin >> v1;
cout << v1 << endl;
cout << "Length of v1: " << v1.length() << endl;
cout << endl;
Vector_3D v2(v1);
cout << v2 << endl;
cout << "Length of v2: " << v2.length() << endl;
Point_3D p1, p2;
cin >> p1 >> p2;
v2 = p1 - p2;
cout << v2 << endl;
cout << "Length of v2: " << v2.length() << endl;
cout << endl;
cout << "v1: " << v1 << endl;
cout << "v2: " << v2 << endl;
cout << "Dot: " << v1.dot(v2) << endl;
cout << endl;
cin >> v2;
Vector_3D v3 = v1.cross(v2);
cout << "v1: " << v1 << endl;
cout << "v2: " << v2 << endl;
cout << "Cross: " << v3 << endl;
cout << endl;
return 0;
}
Example 3: Fixed Point Number & Fixed Point Number Calculator
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
class Fp_Calc; // forward declaration
// Fixed point class declaration
class Fixed_Point
{
private:
long long int m_int_part;
long long int m_frac_part;
unsigned int m_precision;
// utility functions
// set fixed point without checking
void _set(const string &arg_str);
// normalize to m_precision
void _normalize(const unsigned int arg_precision = 0);
public:
Fixed_Point(const long long int &arg_int_part = 0,
const unsigned long long int &arg_frac_part = 0,
const unsigned int &arg_precision = 9);
// Fixed_Point(const string &arg_str);
~Fixed_Point();
// getter & setter
void set_int_part(const long long int arg_int_part);
void set_frac_part(const unsigned long long int arg_frac_part);
void set_precision(const unsigned int arg_precision);
void set(const long long int &arg_int_part,
const unsigned long long int &arg_frac_part,
const unsigned int &arg_precision);
long long int get_int_part() const;
unsigned long long int get_frac_part() const;
unsigned int get_precision() const;
string get_string_value() const;
// arithmetic operators
Fixed_Point operator+(const Fixed_Point &arg_fp) const;
Fixed_Point operator-(const Fixed_Point &arg_fp) const;
Fixed_Point operator+=(const Fixed_Point &arg_fp);
Fixed_Point operator-=(const Fixed_Point &arg_fp);
// conversion operators
operator double() const;
operator float() const;
// assignment operators
Fixed_Point &operator=(const Fixed_Point &arg_fp);
Fixed_Point &operator=(const double &arg_double);
Fixed_Point &operator=(const float &arg_float);
// friend class
friend class Fp_Calc;
// friend function
// formatted output
friend ostream &operator<<(ostream &os, const Fixed_Point &arg_fp);
// formatted input
friend istream &operator>>(istream &is, Fixed_Point &arg_fp);
};
// Fixed point calculator class declaration
class Fp_Calc
{
private:
// define current value
Fixed_Point m_curr_val;
// define input value
Fixed_Point m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and ` ` for none
char m_op;
// calculate result
void _calc_result();
public:
// Constructor
Fp_Calc();
// Copy constructor
Fp_Calc(const Fp_Calc &arg_int_calc);
// Destructor
~Fp_Calc(){}; // no need to do anything
// clear the input value
void clear();
// // set the input value
// void set_input(const string &arg_input);
// add the input value to the current value
void add();
// subtract the input value from the current value
void sub();
// multiply the input value with the current value
void mul();
// divide the current value by the input value
void div();
// assign the input value to the current value
void assign();
// get the current value
Fixed_Point get_curr_val();
// get the current operation
char get_op();
// get the input value
Fixed_Point get_input_val();
// formatted output
friend ostream &operator<<(ostream &os, const Fp_Calc &arg_fp_calc);
// formatted input
friend istream &operator>>(istream &is, Fp_Calc &arg_fp_calc);
};
// Fixed point class implementation
// utility functions
// set fixed point without checking
void Fixed_Point::_set(const string &arg_str)
{
// set integer part
m_int_part = stoll(arg_str.substr(0, arg_str.find('.')));
// set fractional part
m_frac_part = stoull(arg_str.substr(arg_str.find('.') + 1));
// set precision
m_precision = arg_str.length() - arg_str.find('.') - 1;
}
// normalize to precision
void Fixed_Point::_normalize(const unsigned int arg_precision)
{
unsigned int temp_precision = arg_precision;
// if precision is not specified, use the current precision
if (arg_precision == 0)
{
temp_precision = m_precision;
}
// if precision is over the maximum, use the maximum
else if (arg_precision > 9)
{
temp_precision = 9;
}
else
{
temp_precision = arg_precision;
}
// update fractional part
int precision_diff = temp_precision - m_precision;
if (precision_diff > 0)
{
m_frac_part *= pow(10, precision_diff);
}
else if (precision_diff < 0)
{
m_frac_part /= pow(10, -precision_diff);
}
// update m_precision
m_precision = temp_precision;
// handle fractional part overflow
// update integer part
if (m_frac_part >= pow(10, m_precision))
{
m_int_part += m_frac_part / pow(10, m_precision);
m_frac_part %= (int)pow(10, m_precision);
}
// handle fractional part underflow
// update integer part
if (m_frac_part < 0)
{
m_int_part -= 1;
m_frac_part += pow(10, m_precision);
}
}
// Constructor
Fixed_Point::Fixed_Point(const long long int &arg_int_part,
const unsigned long long int &arg_frac_part,
const unsigned int &arg_precision)
: m_int_part(arg_int_part),
m_frac_part(arg_frac_part),
m_precision(arg_precision)
{
}
Fixed_Point::~Fixed_Point()
{
// do nothing
}
// getter & setter
void Fixed_Point::set_int_part(const long long int arg_int_part)
{
m_int_part = arg_int_part;
}
void Fixed_Point::set_frac_part(const unsigned long long int arg_frac_part)
{
m_frac_part = arg_frac_part;
_normalize();
}
void Fixed_Point::set_precision(const unsigned int arg_precision)
{
_normalize(arg_precision);
}
void Fixed_Point::set(const long long int &arg_int_part,
const unsigned long long int &arg_frac_part,
const unsigned int &arg_precision)
{
m_int_part = arg_int_part;
m_frac_part = arg_frac_part;
m_precision = arg_precision;
_normalize();
}
long long int Fixed_Point::get_int_part() const
{
return m_int_part;
}
unsigned long long int Fixed_Point::get_frac_part() const
{
return m_frac_part;
}
unsigned int Fixed_Point::get_precision() const
{
return m_precision;
}
string Fixed_Point::get_string_value() const
{
string str_int_part = to_string(m_int_part);
string str_frac_part = to_string(m_frac_part);
// if precision is not specified, use the current precision
if (m_precision == 0)
{
return str_int_part;
}
// if precision is 1, return integer part and fractional part
else if (m_precision == 1)
{
return str_int_part + "." + str_frac_part;
}
// if precision is over 1, return integer part and fractional part with
// specified precision
else
{
// if fractional part is 0, return integer part
if (str_frac_part == "0")
{
return str_int_part;
}
// if fractional part is not 0, return integer part and fractional part
else
{
// if fractional part is less than precision, add 0 to the front
if (str_frac_part.length() < m_precision)
{
str_frac_part = string(m_precision - str_frac_part.length(), '0')
+ str_frac_part;
}
// if fractional part is more than precision, remove the end
else if (str_frac_part.length() > m_precision)
{
str_frac_part = str_frac_part.substr(0, m_precision);
}
return str_int_part + "." + str_frac_part;
}
}
}
Fixed_Point Fixed_Point::operator+(const Fixed_Point &arg_fixed_point) const
{
Fixed_Point result(*this);
result += arg_fixed_point;
return result;
}
Fixed_Point Fixed_Point::operator-(const Fixed_Point &arg_fixed_point) const
{
Fixed_Point result(*this);
result -= arg_fixed_point;
return result;
}
Fixed_Point Fixed_Point::operator+=(const Fixed_Point &arg_fixed_point)
{
Fixed_Point normalized_arg(arg_fixed_point);
unsigned int max_precision = max(m_precision,
normalized_arg.m_precision);
set_precision(max_precision);
normalized_arg.set_precision(max_precision);
m_precision = max_precision;
m_int_part = m_int_part + normalized_arg.m_int_part;
m_frac_part = m_frac_part + normalized_arg.m_frac_part;
_normalize();
return *this;
}
Fixed_Point Fixed_Point::operator-=(const Fixed_Point &arg_fixed_point)
{
Fixed_Point normalized_arg(arg_fixed_point);
unsigned int max_precision = max(m_precision,
normalized_arg.m_precision);
set_precision(max_precision);
normalized_arg.set_precision(max_precision);
m_int_part = m_int_part - normalized_arg.m_int_part;
m_frac_part = m_frac_part - normalized_arg.m_frac_part;
_normalize();
return *this;
}
Fixed_Point::operator double() const
{
return double(m_int_part) + double(m_frac_part) / pow(10, m_precision);
}
Fixed_Point::operator float() const
{
return float(m_int_part) + float(m_frac_part) / pow(10, m_precision);
}
Fixed_Point &Fixed_Point::operator=(const Fixed_Point &arg_fp)
{
m_int_part = arg_fp.m_int_part;
m_frac_part = arg_fp.m_frac_part;
m_precision = arg_fp.m_precision;
return *this;
}
Fixed_Point &Fixed_Point::operator=(const double &arg_double)
{
_set(to_string(arg_double));
_normalize();
return *this;
}
Fixed_Point &Fixed_Point::operator=(const float &arg_float)
{
_set(to_string(arg_float));
_normalize();
return *this;
}
// formated output
ostream &operator<<(ostream &arg_os, const Fixed_Point &arg_fixed_point)
{
arg_os << arg_fixed_point.get_string_value(); // reuse get_string_value()
return arg_os;
}
// formated input
istream &operator>>(istream &arg_is, Fixed_Point &arg_fixed_point)
{
string str_value;
arg_is >> str_value;
arg_fixed_point._set(str_value); // reuse _set()
arg_fixed_point._normalize();
return arg_is;
}
// Fp_Calc class implementation
// Constructor
Fp_Calc::Fp_Calc()
: m_curr_val(), m_input_val(), m_op(' ')
{
}
// Copy constructor
Fp_Calc::Fp_Calc(const Fp_Calc &arg_int_calc)
: m_curr_val(arg_int_calc.m_curr_val),
m_input_val(arg_int_calc.m_input_val),
m_op(arg_int_calc.m_op)
{
}
// calculate the result
void Fp_Calc::_calc_result()
{
switch (m_op)
{
case '+':
m_curr_val += m_input_val;
break;
case '-':
m_curr_val -= m_input_val;
break;
case ' ':
m_curr_val = m_input_val;
break;
default:
break;
}
}
// clear the input value
void Fp_Calc::clear()
{
m_input_val = Fixed_Point();
}
// // set the input value
// void Fp_Calc::set_input(const string &arg_input_val)
// {
// m_input_val = Fixed_Point(arg_input_val);
// }
// add the input value to the current value
void Fp_Calc::add()
{
_calc_result();
m_op = '+';
}
// subtract the input value from the current value
void Fp_Calc::sub()
{
_calc_result();
m_op = '-';
}
// multiply the input value with the current value
void Fp_Calc::mul()
{
_calc_result();
m_op = '*';
}
// divide the current value by the input value
void Fp_Calc::div()
{
_calc_result();
m_op = '/';
}
// assign the input value to the current value
void Fp_Calc::assign()
{
_calc_result();
m_op = ' ';
}
// get the current value
Fixed_Point Fp_Calc::get_curr_val()
{
return m_curr_val;
}
// get the current operation
char Fp_Calc::get_op()
{
return m_op;
}
// get the input value
Fixed_Point Fp_Calc::get_input_val()
{
return m_input_val;
}
// formated output
ostream &operator<<(ostream &arg_os, Fp_Calc &arg_fp_calc)
{
arg_os << arg_fp_calc.get_curr_val();
return arg_os;
}
// formated input
istream &operator>>(istream &arg_is, Fp_Calc &arg_fp_calc)
{
arg_is >> arg_fp_calc.m_input_val;
return arg_is;
}
// main function
int main()
{
// create an instance of the class
Fp_Calc calc;
// set the input value
cin >> calc;
// get the input value
cout << "Input: " << calc.get_input_val() << endl;
// add the input value to the current value
calc.add();
// get current op
cout << '\'' << calc.get_op() << '\'' << endl;
// set another input value
cin >> calc;
// get the input value
cout << "Input: " << calc.get_input_val() << endl;
// clear the input value
calc.clear();
cout << "clear" << endl;
// set the input value
cin >> calc;
// get the input value
cout << "Input: " << calc.get_input_val() << endl;
// subtract the input value from the current value
calc.sub();
// get current op
cout << '\'' << calc.get_op() << '\'' << endl;
// print the result
cout << "Result: " << calc << endl;
// set another input value
cin >> calc;
// get the input value
cout << "Input: " << calc.get_input_val() << endl;
// compute the result
calc.assign();
// print the result
cout << "Result: " << calc << endl;
}
Lab 6: Complex Number Calculator
Lab 6-1: Enhanced Complex Numbers (40%)
- 輸入:
- 以
double格式輸入複數的實數及虛數部分,以空格分開,一行輸入一個複數 - 以
char格式輸入複數的運算子,包含+、-、*、/,一行輸入一個運算子 - 複數與運算子以交錯的方式輸入,一行輸入一個複數接著一個運算子,倒數兩行為複數與完成輸入指令
- 輸入 Ctrl+D 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
^Z) 再輸入 Enter (Format 中的⏎) 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
- 以
- 輸出:
- 顯示運算複數的結果
- 格式請參考 Format 中的說明
- 若虛數部分為 0 則僅顯示實數部分
- 虛數及實數部分皆以預設
double格式顯示
- 顯示運算複數的結果
- 檔名:
lab6-1_<學號>.cpp(e.g.lab6-1_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果
- 使用者不需要處理錯誤輸入
- 請使用 pseudo code 提供的 main function 來處理輸入與輸出
- 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Format
<real 1> <imag 1>⏎
<op 1>⏎
<real 2> <imag 2>⏎
<op 2>⏎
...
<real n-1> <imag n-1>⏎
<op n-1>⏎
<real n> <imag n>⏎
^Z⏎
(-)<real result> (+|-) (<imag result>i)
Example
$ ./a.out
1.0 0.0⏎
^Z⏎
1
$ ./a.out
0.0 1.0⏎
^Z⏎
0 + 1i⏎
$ ./a.out
1.0 0.0⏎
+⏎
2.0 1.1⏎
-⏎
-3.0 -2.2⏎
*⏎
4.3 2.1⏎
/⏎
-1.2 -3.4⏎
^Z⏎
-8.74846 + 2.46231i
$ ./a.out
1.0 0.0⏎
+⏎
2.0 1.1⏎
-⏎
-3.0 -2.2⏎
*⏎
4.3 2.1⏎
/⏎
-1.2 3.4⏎
^Z⏎
5.26477 - 7.40815i
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// subtract assignment operator
Complex &operator-=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// divide assignment operator
Complex &operator/=(const Complex &arg_c);
// add function
Complex operator+(const Complex &arg_c) const;
// subtract function
Complex operator-(const Complex &arg_c) const;
// multiply function
Complex operator*(const Complex &arg_c) const;
// divide function
Complex operator/(const Complex &arg_c) const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: be careful about the format of input
// hint: use `stod` to convert string to double
friend istream &operator>>(istream &arg_is, Complex &arg_c);
};
// used for process the test cases, do not modify
int main()
{
string input;
Complex result_complex;
char op = ' ';
while (getline(cin, input))
{
// input is a operation
if (input == "+" || input == "-" || input == "*" || input == "/")
{
op = input[0];
continue;
}
else if (input.empty())
{
continue;
}
// input is a complex number
else
{
stringstream ss(input);
Complex current_complex;
ss >> current_complex;
switch (op)
{
case '+':
result_complex += current_complex;
break;
case '-':
result_complex -= current_complex;
break;
case '*':
result_complex *= current_complex;
break;
case '/':
result_complex /= current_complex;
break;
case ' ':
result_complex = current_complex;
break;
default:
cerr << "Error: unknown operation" << endl;
return 1;
}
}
}
cout << endl;
cout << result_complex << endl;
return 0;
}
Reference Code:
陳誼倫(110021127)
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0, const double &arg_imag = 0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
~Complex() {}
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// subtract assignment operator
Complex &operator-=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// divide assignment operator
Complex &operator/=(const Complex &arg_c);
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: be careful about the format of input
// hint: use `stod` to convert string to double
friend istream &operator>>(istream &arg_is, Complex &arg_c);
};
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag) {}
Complex::Complex(const Complex &arg_point)
: m_real(arg_point.m_real), m_imag(arg_point.m_imag) {}
Complex &Complex::operator=(const Complex &arg_c)
{
this->m_real = arg_c.m_real;
this->m_imag = arg_c.m_imag;
return *this;
}
Complex &Complex::operator+=(const Complex &arg_c)
{
this->m_real += arg_c.m_real;
this->m_imag += arg_c.m_imag;
return *this;
}
Complex &Complex::operator-=(const Complex &arg_c)
{
this->m_real -= arg_c.m_real;
this->m_imag -= arg_c.m_imag;
return *this;
}
Complex &Complex::operator*=(const Complex &arg_c)
{
double _real = this->m_real, _imag = this->m_imag;
this->m_real = (_real * arg_c.m_real) - (_imag * arg_c.m_imag);
this->m_imag = (_real * arg_c.m_imag) + (_imag * arg_c.m_real);
return *this;
}
Complex &Complex::operator/=(const Complex &arg_c)
{
double _real = this->m_real, _imag = this->m_imag;
this->m_real = ((_real * arg_c.m_real) + (_imag * arg_c.m_imag))
/ ((arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag));
this->m_imag = ((-_real * arg_c.m_imag) + (_imag * arg_c.m_real))
/ ((arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag));
return *this;
}
std::ostream &operator<<(std::ostream &arg_os, const Complex &arg_point)
{
if (arg_point.m_imag == 0)
{
arg_os << arg_point.m_real;
return arg_os;
}
else if (arg_point.m_imag < 0)
{
arg_os << arg_point.m_real << " - " << -arg_point.m_imag << "i ";
return arg_os;
}
else
{
arg_os << arg_point.m_real << " + " << arg_point.m_imag << "i ";
return arg_os;
}
}
// read the coordinate of a point from the input, format: (x, y) and ignore space
std::istream &operator>>(std::istream &arg_is, Complex &arg_point)
{
string str_x, str_y, temp;
if (getline(arg_is, str_x, ' '))
{
if (getline(arg_is, str_y, ' '))
{
arg_point.m_real = stod(str_x);
arg_point.m_imag = stod(str_y);
}
}
return arg_is;
}
// used for process the test cases, do not modify
int main()
{
string input;
Complex result_complex;
char op = ' ';
while (getline(cin, input))
{
// input is a operation
if (input == "+" || input == "-" || input == "*" || input == "/")
{
op = input[0];
continue;
}
else if (input.empty())
{
continue;
}
// input is a complex number
else
{
stringstream ss(input);
Complex current_complex;
ss >> current_complex;
switch (op)
{
case '+':
result_complex += current_complex;
break;
case '-':
result_complex -= current_complex;
break;
case '*':
result_complex *= current_complex;
break;
case '/':
result_complex /= current_complex;
break;
case ' ':
result_complex = current_complex;
break;
default:
cerr << "Error: unknown operation" << endl;
return 1;
}
}
}
cout << endl;
cout << result_complex << endl;
return 0;
}
林恩佑(109021107)
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with double precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// subtract assignment operator
Complex &operator-=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// divide assignment operator
Complex &operator/=(const Complex &arg_c);
// add function
Complex operator+(const Complex &arg_c) const;
// subtract function
Complex operator-(const Complex &arg_c) const;
// multiply function
Complex operator*(const Complex &arg_c) const;
// divide function
Complex operator/(const Complex &arg_c) const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: be careful about the format of input
// hint: use stod to convert string to double
friend istream &operator>>(istream &arg_is, Complex &arg_c);
};
Complex::Complex(const double &arg_real, const double &arg_image)
: m_real(arg_real), m_imag(arg_image)
{
}
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
Complex &Complex::operator=(const Complex &arg_c)
{
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
Complex &Complex::operator+=(const Complex &arg_c)
{
m_real += arg_c.m_real;
m_imag += arg_c.m_imag;
return *this;
}
Complex &Complex::operator-=(const Complex &arg_c)
{
m_real -= arg_c.m_real;
m_imag -= arg_c.m_imag;
return *this;
}
Complex &Complex::operator*=(const Complex &arg_c)
{
Complex a;
a.m_real = m_real;
a.m_imag = m_imag;
m_real = a.m_real * arg_c.m_real - a.m_imag * arg_c.m_imag;
m_imag = a.m_real * arg_c.m_imag + arg_c.m_real * a.m_imag;
return *this;
}
Complex &Complex::operator/=(const Complex &arg_c)
{
Complex a;
a.m_real = m_real;
a.m_imag = m_imag;
m_real = (a.m_real * arg_c.m_real + a.m_imag * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
m_imag = (arg_c.m_real * a.m_imag - a.m_real * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
return *this;
}
ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag == 0)
{
arg_os << arg_c.m_real;
}
else if (arg_c.m_imag < 0)
{
arg_os << arg_c.m_real << " - " << 0.0 - arg_c.m_imag << "i";
}
else
{
arg_os << arg_c.m_real << " + " << arg_c.m_imag << "i";
}
return arg_os;
}
istream &operator>>(istream &arg_is, Complex &arg_c)
{
string strs;
size_t sz;
arg_c = {0, 0};
arg_is >> strs;
try
{
arg_c.m_real = stod(strs);
}
catch (const invalid_argument &ia)
{
}
strs = "";
arg_is >> strs;
try
{
arg_c.m_imag = stod(strs);
}
catch (const invalid_argument &ia)
{
}
return arg_is;
}
// used for process the test cases, do not modify
int main()
{
string input;
Complex result_complex;
char op = ' ';
while (getline(cin, input))
{
// input is a operation
if (input == "+" || input == "-" || input == "*" || input == "/")
{
op = input[0];
continue;
}
else if (input.empty())
{
continue;
}
// input is a complex number
else
{
stringstream ss(input);
Complex current_complex;
ss >> current_complex;
switch (op)
{
case '+':
result_complex += current_complex;
break;
case '-':
result_complex -= current_complex;
break;
case '*':
result_complex *= current_complex;
break;
case '/':
result_complex /= current_complex;
break;
case ' ':
result_complex = current_complex;
break;
default:
cerr << "Error: unknown operation" << endl;
return 1;
}
}
}
cout << endl;
cout << result_complex << endl;
return 0;
}
Lab 6-2: Simple Complex Number Calculator (40%)
- 輸入:
- 以
double格式輸入複數的實數及虛數部分,以空格分開,一行輸入一個複數 - 以
char格式輸入複數的運算子,包含+、-、*、/,一行輸入一個運算子 - 複數與運算子以交錯的方式輸入,一行輸入一個複數接著一個運算子,倒數一行為複數
- 輸入 Ctrl+D 結束程式
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
^Z) 再輸入 Enter (Format 中的⏎) 結束程式
- 以
- 輸出:
- 顯示運算複數的結果
- 複數的格式為
(-)<real result> (+|-) (<imag result>i) - 若輸入運算子、需顯示之前運算的結果,如 Example 的範例
- 檔名:
lab6-2_<學號>.cpp(e.g.lab6-2_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果或錯誤訊息
- 使用者不需要處理錯誤輸入
- 請使用 pseudo code 提供的
main及Complex_Calc::set_input來處理輸入與輸出 - 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Format
<real 1> <imag 1>⏎
<result 1>
<op 1>⏎
<result 1>
<real 2> <imag 2>⏎
<result 2>
<op 2>⏎
<result 2>
...
<real n-1> <imag n-1>⏎
<result n-1>
<op n-1>⏎
<result n-1>
<real n> <imag n>⏎
<result n>
^Z⏎
Example
$ ./a.out
1.0 0.0⏎
1
^Z⏎
$ ./a.out
0.0 1.0⏎
0 + 1i⏎
^Z⏎
$ ./a.out
1.0 0.0⏎
1
+⏎
1
2.0 1.1⏎
3 + 1.1i
-⏎
3 + 1.1i
-3.0 -2.2⏎
6 + 3.3i
*⏎
6 + 3.3i
4.3 2.1⏎
18.87 + 26.79i
/⏎
18.87 + 26.79i
-1.2 -3.4⏎
-8.74846 + 2.46231i
^Z⏎
$ ./a.out
1.0 0.0⏎
1
+⏎
1
2.0 1.1⏎
3 + 1.1i
-⏎
3 + 1.1i
-3.0 -2.2⏎
6 + 3.3i
*⏎
6 + 3.3i
4.3 2.1⏎
18.87 + 26.79i
/⏎
18.87 + 26.79i
-1.2 3.4⏎
5.26477 - 7.40815i
^Z⏎
$
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
using namespace std;
class Complex_Calc;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// subtract assignment operator
Complex &operator-=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// divide assignment operator
Complex &operator/=(const Complex &arg_c);
// add function
Complex operator+(const Complex &arg_c) const;
// subtract function
Complex operator-(const Complex &arg_c) const;
// multiply function
Complex operator*(const Complex &arg_c) const;
// divide function
Complex operator/(const Complex &arg_c) const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: be careful about the format of input
// hint: use `stod` to convert string to double
friend istream &operator>>(istream &arg_is, Complex &arg_c);
friend class Complex_Calc;
};
// Complex calculator class declaration
class Complex_Calc
{
private:
// define current value
Complex m_curr_val;
// define input value
Complex m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and `=`
char m_op;
// calculate result
void _calc_result();
// operation functions
// add the input value to the current value
void _add();
// subtract the input value from the current value
void _sub();
// multiply the input value with the current value
void _mul();
// divide the current value by the input value
void _div();
// assign the input value to the current value
void _assign();
public:
// Constructor
Complex_Calc();
// Copy constructor
Complex_Calc(const Complex_Calc &arg_int_calc);
// Destructor
~Complex_Calc(){}; // no need to do anything
// set input value or operation
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc);
};
// parse the test cases, do not modify belows
void Complex_Calc::set_input(const string &arg_input)
{
// input is empty, read again
if (arg_input.empty())
{
return;
}
// input is a operation
else if (arg_input == "+" || arg_input == "-" || arg_input == "*"
|| arg_input == "/" || arg_input == "=")
{
// set the activated operation
// as the same as the user press the op button
switch (arg_input[0])
{
case '+':
_add();
break;
case '-':
_sub();
break;
case '*':
_mul();
break;
case '/':
_div();
break;
case '=':
_assign();
break;
}
}
// input is a complex number
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
else
{
stringstream ss(arg_input);
ss >> m_input_val;
_calc_result();
}
}
// main function
int main()
{
// create an instance of the class
Complex_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
Reference Code:
林恩佑(109021107)
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
using namespace std;
class Complex_Calc;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with double precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// subtract assignment operator
Complex &operator-=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// divide assignment operator
Complex &operator/=(const Complex &arg_c);
// add function
Complex operator+(const Complex &arg_c) const;
// subtract function
Complex operator-(const Complex &arg_c) const;
// multiply function
Complex operator*(const Complex &arg_c) const;
// divide function
Complex operator/(const Complex &arg_c) const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: be careful about the format of input
// hint: use stod to convert string to double
friend istream &operator>>(istream &arg_is, Complex &arg_c);
friend class Complex_Calc;
};
Complex::Complex(const double &arg_real, const double &arg_image)
: m_real(arg_real), m_imag(arg_image)
{
}
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
Complex &Complex::operator=(const Complex &arg_c)
{
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
Complex &Complex::operator+=(const Complex &arg_c)
{
m_real += arg_c.m_real;
m_imag += arg_c.m_imag;
return *this;
}
Complex &Complex::operator-=(const Complex &arg_c)
{
m_real -= arg_c.m_real;
m_imag -= arg_c.m_imag;
return *this;
}
Complex &Complex::operator*=(const Complex &arg_c)
{
Complex a;
a.m_real = m_real;
a.m_imag = m_imag;
m_real = a.m_real * arg_c.m_real - a.m_imag * arg_c.m_imag;
m_imag = a.m_real * arg_c.m_imag + arg_c.m_real * a.m_imag;
return *this;
}
Complex &Complex::operator/=(const Complex &arg_c)
{
Complex a;
a.m_real = m_real;
a.m_imag = m_imag;
m_real = (a.m_real * arg_c.m_real + a.m_imag * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
m_imag = (arg_c.m_real * a.m_imag - a.m_real * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
return *this;
}
ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag == 0)
{
arg_os << arg_c.m_real;
}
else if (arg_c.m_imag < 0)
{
arg_os << arg_c.m_real << " - " << 0.0 - arg_c.m_imag << "i";
}
else
{
arg_os << arg_c.m_real << " + " << arg_c.m_imag << "i";
}
return arg_os;
}
istream &operator>>(istream &arg_is, Complex &arg_c)
{
string strs;
size_t sz;
arg_c = {0, 0};
arg_is >> strs;
try
{
arg_c.m_real = stod(strs);
}
catch (const invalid_argument &ia)
{
}
strs = "";
arg_is >> strs;
try
{
arg_c.m_imag = stod(strs);
}
catch (const invalid_argument &ia)
{
}
return arg_is;
}
// Complex calculator class declaration
class Complex_Calc
{
private:
// define current value
Complex m_curr_val;
// define input value
Complex m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and `=`
char m_op;
// calculate result
void _calc_result();
// operation functions
// add the input value to the current value
void _add();
// subtract the input value from the current value
void _sub();
// multiply the input value with the current value
void _mul();
// divide the current value by the input value
void _div();
// assign the input value to the current value
void _assign();
public:
// Constructor
Complex_Calc();
// Copy constructor
Complex_Calc(const Complex_Calc &arg_int_calc);
// Destructor
~Complex_Calc(){}; // no need to do anything
// set input value or operation
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc);
};
Complex_Calc::Complex_Calc()
: m_curr_val(), m_input_val(), m_op('=')
{
}
Complex_Calc::Complex_Calc(const Complex_Calc &arg_int_calc)
: m_curr_val(arg_int_calc.m_curr_val),
m_input_val(arg_int_calc.m_input_val),
m_op(arg_int_calc.m_op)
{
}
void Complex_Calc::_calc_result()
{
switch (m_op)
{
case '+':
m_curr_val += m_input_val;
break;
case '-':
m_curr_val -= m_input_val;
break;
case '*':
m_curr_val *= m_input_val;
break;
case '/':
m_curr_val /= m_input_val;
break;
case '=':
m_curr_val = m_input_val;
break;
default:
break;
}
}
void Complex_Calc::_add()
{
m_op = '+';
}
void Complex_Calc::_sub()
{
m_op = '-';
}
void Complex_Calc::_mul()
{
m_op = '*';
}
void Complex_Calc::_div()
{
m_op = '/';
}
void Complex_Calc::_assign()
{
m_op = '=';
}
ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc)
{
Complex arg_c = arg_comp_calc.m_curr_val;
arg_os << arg_c;
return arg_os;
}
/*
ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc){
if (arg_c.m_imag==0){
arg_os << arg_c.m_real <<endl;
}
else if (arg_c.m_imag<0){
arg_c.m_imag*=(-1);
arg_os<<arg_c.m_real<<" - "<<arg_c.m_imag<<" i"<<endl;
}
else{
arg_os << arg_c.m_real << " + " << arg_c.m_imag <<" i"<<endl;
}
return arg_os;
}
*/
// parse the test cases, do not modify belows
void Complex_Calc::set_input(const string &arg_input)
{
// input is empty, read again
if (arg_input.empty())
{
return;
}
// input is a operation
else if (arg_input == "+" || arg_input == "-" || arg_input == "*"
|| arg_input == "/" || arg_input == "=")
{
// set the activated operation
// as the same as the user press the op button
switch (arg_input[0])
{
case '+':
_add();
break;
case '-':
_sub();
break;
case '*':
_mul();
break;
case '/':
_div();
break;
case '=':
_assign();
break;
}
}
// input is a complex number
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
else
{
stringstream ss(arg_input);
ss >> m_input_val;
_calc_result();
}
}
// main function
int main()
{
// create an instance of the class
Complex_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
TA
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
using namespace std;
class Complex_Calc;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// subtract assignment operator
Complex &operator-=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// divide assignment operator
Complex &operator/=(const Complex &arg_c);
// add function
Complex operator+(const Complex &arg_c) const;
// subtract function
Complex operator-(const Complex &arg_c) const;
// multiply function
Complex operator*(const Complex &arg_c) const;
// divide function
Complex operator/(const Complex &arg_c) const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
friend class Complex_Calc;
};
// Complex calculator class declaration
class Complex_Calc
{
private:
// define current value
Complex m_curr_val;
// define input value
Complex m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and `=`
char m_op;
// define input status, turns `op` for true and turns `value` for false
bool m_op_input;
// calculate result
void _calc_result();
// operation functions
// set activation op to add
void _add();
// set activation op to subtract
void _sub();
// set activation op to multiply
void _mul();
// set activation op to divide
void _div();
// set activation op to assign
void _assign();
public:
// Constructor
Complex_Calc();
// Copy constructor
Complex_Calc(const Complex_Calc &arg_int_calc);
// Destructor
~Complex_Calc(){}; // no need to do anything
// set input value or operation
// as the same as the user input number or operation
// into the calculator
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc);
};
// error and exit
void error_and_exit()
{
cerr << "Error: Invalid input" << endl;
exit(1);
}
// Complex class implementation
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
// Copy constructor
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
// assignment operator
Complex &Complex::operator=(const Complex &arg_c)
{
if (this == &arg_c) // self-assignment
return *this;
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
// add assignment operator
Complex &Complex::operator+=(const Complex &arg_c)
{
m_real += arg_c.m_real;
m_imag += arg_c.m_imag;
return *this;
}
// subtract assignment operator
Complex &Complex::operator-=(const Complex &arg_c)
{
m_real -= arg_c.m_real;
m_imag -= arg_c.m_imag;
return *this;
}
// multiply assignment operator
Complex &Complex::operator*=(const Complex &arg_c)
{
double real = m_real * arg_c.m_real - m_imag * arg_c.m_imag;
double imag = m_real * arg_c.m_imag + m_imag * arg_c.m_real;
m_real = real;
m_imag = imag;
return *this;
}
// divide assignment operator
Complex &Complex::operator/=(const Complex &arg_c)
{
if (arg_c.m_real == 0 && arg_c.m_imag == 0)
error_and_exit();
double real = (m_real * arg_c.m_real + m_imag * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
double imag = (m_imag * arg_c.m_real - m_real * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
m_real = real;
m_imag = imag;
return *this;
}
// add function
Complex Complex::operator+(const Complex &arg_c) const
{
Complex c(*this);
c += arg_c;
return c;
}
// subtract function
Complex Complex::operator-(const Complex &arg_c) const
{
Complex c(*this);
c -= arg_c;
return c;
}
// multiply function
Complex Complex::operator*(const Complex &arg_c) const
{
Complex c(*this);
c *= arg_c;
return c;
}
// divide function
Complex Complex::operator/(const Complex &arg_c) const
{
Complex c(*this);
c /= arg_c;
return c;
}
// cout `<<` operator for print complex number
// note: be careful about the format of output
ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag > 0)
{
arg_os << arg_c.m_real << " + " << arg_c.m_imag << "i";
}
else if (arg_c.m_imag < 0)
{
arg_os << arg_c.m_real << " - " << -arg_c.m_imag << "i";
}
else
{
arg_os << arg_c.m_real;
}
return arg_os;
}
// cin `>>` operator for input complex number
// note: be careful about the format of input
istream &operator>>(istream &arg_is, Complex &arg_c)
{
double input_real, input_imag;
arg_is >> input_real;
arg_is >> input_imag;
arg_c.m_real = input_real;
arg_c.m_imag = input_imag;
return arg_is;
}
// Complex_Calc class implementation
// Constructor
Complex_Calc::Complex_Calc()
: m_curr_val(), m_input_val(), m_op('='), m_op_input(false)
{
}
// Copy constructor
Complex_Calc::Complex_Calc(const Complex_Calc &arg_int_calc)
: m_curr_val(arg_int_calc.m_curr_val),
m_input_val(arg_int_calc.m_input_val),
m_op(arg_int_calc.m_op),
m_op_input(arg_int_calc.m_op_input)
{
}
// parse the test cases, do not modify belows
void Complex_Calc::set_input(const string &arg_input)
{
// input is empty, read again
if (arg_input.empty())
{
return;
}
// input is a operation
else if (arg_input == "+" || arg_input == "-" || arg_input == "*"
|| arg_input == "/" || arg_input == "=")
{
// set the activated operation
// as the same as the user press the op button
switch (arg_input[0])
{
case '+':
_add();
break;
case '-':
_sub();
break;
case '*':
_mul();
break;
case '/':
_div();
break;
case '=':
_assign();
break;
}
}
// input is a complex number
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
else
{
stringstream ss(arg_input);
ss >> m_input_val;
_calc_result();
}
}
void Complex_Calc::_calc_result()
{
switch (m_op)
{
case '+':
m_curr_val += m_input_val;
break;
case '-':
m_curr_val -= m_input_val;
break;
case '*':
m_curr_val *= m_input_val;
break;
case '/':
m_curr_val /= m_input_val;
break;
case '=':
m_curr_val = m_input_val;
break;
}
}
// add the input value to the current value
void Complex_Calc::_add()
{
m_op = '+';
}
// subtract the input value from the current value
void Complex_Calc::_sub()
{
m_op = '-';
}
// multiply the input value with the current value
void Complex_Calc::_mul()
{
m_op = '*';
}
// divide the current value by the input value
void Complex_Calc::_div()
{
m_op = '/';
}
// assign the input value to the current value
void Complex_Calc::_assign()
{
m_op = '=';
}
// cout `<<` operator for print calculator status
ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc)
{
arg_os << arg_comp_calc.m_curr_val;
return arg_os;
}
// main function
int main()
{
// create an instance of the class
Complex_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
Lab 6-3: Enhanced Complex Number Calculator (20%)
- 輸入:
- 以
double格式輸入複數的實數及虛數部分,以空格分開,一行輸入一個複數 - 以
char格式輸入複數的運算子,包含+、-、*、/,一行輸入一個運算子 - 複數與運算子以交錯的方式輸入,一行輸入一個複數接著一個運算子,倒數一行為複數
- 在任一行輸入 Ctrl+D 結束程式
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
^Z) 再輸入 Enter (Format 中的⏎) 結束程式
- 程式輸入以行為單位,每行輸入為任何有效的
string格式
- 以
- 輸出:
- 顯示運算複數的結果
- 複數的格式為
(-)<real result> (+|-) (<imag result>i) - 若輸入運算子、需顯示之前運算的結果,如 Example 的範例
- 若使用者輸入的複數或運算子不正確,則顯示錯誤訊息
Error: Invalid input並結束程式
- 檔名:
lab6-3_<學號>.cpp(e.g.lab6-3_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果或錯誤訊息
- 程式僅需處裡輸入錯誤的例外狀況,如輸入的複數或運算子不正確,其餘錯誤不須處裡
- 請基於 pseudo code 提供的
main及Complex_Calc::set_input進行修改來處理輸入與輸出 - 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Format
<real 1> <imag 1>⏎
<result 1>
<op 1>⏎
<result 1>
<real 2> <imag 2>⏎
<result 2>
<op 2>⏎
<result 2>
...
<real n-1> <imag n-1>⏎
<result n-1>
<op n-1>⏎
<result n-1>
<real n> <imag n>⏎
<result n>
^Z⏎
Example
Normal
$ ./a.out
1.0 0.0⏎
1
^Z⏎
$ ./a.out
0.0 1.0⏎
0 + 1i⏎
^Z⏎
$ ./a.out
1.0 0.0⏎
1
+⏎
1
^Z⏎
$ ./a.out
^Z⏎
$ ./a.out
1.0 0.0⏎
1
+⏎
1
2.0 1.1⏎
3 + 1.1i
-⏎
3 + 1.1i
-3.0 -2.2⏎
6 + 3.3i
*⏎
6 + 3.3i
4.3 2.1⏎
18.87 + 26.79i
/⏎
18.87 + 26.79i
-1.2 -3.4⏎
-8.74846 + 2.46231i
^Z⏎
$ ./a.out
1.0 0.0⏎
1
+⏎
1
2.0 1.1⏎
3 + 1.1i
-⏎
3 + 1.1i
-3.0 -2.2⏎
6 + 3.3i
*⏎
6 + 3.3i
4.3 2.1⏎
18.87 + 26.79i
/⏎
18.87 + 26.79i
-1.2 3.4⏎
5.26477 - 7.40815i
^Z⏎
$
Exception Handling
$ ./a.out
+⏎
Error: Invalid input
$
$ ./a.out
1.0 0.0⏎
1
1.0 0.0⏎
Error: Invalid input
$
$ ./a.out
1.0 0.0⏎
1
+⏎
1
+⏎
Error: Invalid input
$
$ ./a.out
1.0 2.0 3.0⏎
Error: Invalid input
$
$ ./a.out
1.0 2.0⏎
1 + 2i
sdafsdagret⏎
Error: Invalid input
$
$ ./a.out
sdoifjwepoirjpwoie⏎
Error: Invalid input
$
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
using namespace std;
class Complex_Calc;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// subtract assignment operator
Complex &operator-=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// divide assignment operator
Complex &operator/=(const Complex &arg_c);
// add function
Complex operator+(const Complex &arg_c) const;
// subtract function
Complex operator-(const Complex &arg_c) const;
// multiply function
Complex operator*(const Complex &arg_c) const;
// divide function
Complex operator/(const Complex &arg_c) const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
friend class Complex_Calc;
};
// Complex calculator class declaration
class Complex_Calc
{
private:
// define current value
Complex m_curr_val;
// define input value
Complex m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and `=`
char m_op;
// define input status, truns `op` for true and turns `value` for false
bool m_op_input;
// calculate result
void _calc_result();
// operation functions
// set activation op to add
void _add();
// set activation op to subtract
void _sub();
// set activation op to multiply
void _mul();
// set activation op to divide
void _div();
// set activation op to assign
void _assign();
public:
// Constructor
Complex_Calc();
// Copy constructor
Complex_Calc(const Complex_Calc &arg_int_calc);
// Destructor
~Complex_Calc(){}; // no need to do anything
// set input value or operation
// as the same as the user input number or operation
// into the calculator
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc);
};
// error and exit
void error_and_exit()
{
cerr << "Error: Invalid input" << endl;
exit(1);
}
void Complex_Calc::set_input(const string &arg_input)
{
// input is empty, read again
if (arg_input.empty())
{
return;
}
// input is a operator in right turn
// set the activated operation
// as the same as the user press the op button
// set to 'input a complex number' turn
// input is a complex number in right turn
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
// else, input is invalid
else
{
error_and_exit();
}
}
// main function
int main()
{
// create an instance of the class
Complex_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
Reference Code:
林元鴻(110021120)
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
using namespace std;
class Complex_Calc;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0)
{
m_real = arg_real;
m_imag = arg_imag;
}
// Copy constructor
Complex(const Complex &arg_c)
{
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
}
// assignment operator
Complex &operator=(const Complex &arg_c)
{
m_imag = arg_c.m_imag;
m_real = arg_c.m_real;
return *this;
}
// add assignment operator
Complex &operator+=(const Complex &arg_c)
{
m_imag = m_imag + arg_c.m_imag;
m_real = m_real + arg_c.m_real;
return *this;
}
// subtract assignment operator
Complex &operator-=(const Complex &arg_c)
{
m_imag = m_imag - arg_c.m_imag;
m_real = m_real - arg_c.m_real;
return *this;
}
// multiply assignment operator
Complex &operator*=(const Complex &arg_c)
{
Complex p;
p.m_real = (m_real * arg_c.m_real) - (m_imag * arg_c.m_imag);
p.m_imag = (m_real * arg_c.m_imag) + (m_imag * arg_c.m_real);
m_imag = p.m_imag;
m_real = p.m_real;
return *this;
}
// divide assignment operator
Complex &operator/=(const Complex &arg_c)
{
Complex p;
p.m_real = (arg_c.m_real * m_real + m_imag * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
p.m_imag = (arg_c.m_real * m_imag - m_real * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
m_imag = p.m_imag;
m_real = p.m_real;
return *this;
}
// add function
Complex operator+(const Complex &arg_c) const
{
Complex p;
p.m_imag = m_imag + arg_c.m_imag;
p.m_real = m_real + arg_c.m_real;
return p;
}
// subtract function
Complex operator-(const Complex &arg_c) const
{
Complex p;
p.m_imag = m_imag - arg_c.m_imag;
p.m_real = m_real - arg_c.m_real;
return p;
}
// multiply function
Complex operator*(const Complex &arg_c) const
{
Complex p;
p.m_real = (m_real * arg_c.m_real) - (m_imag * arg_c.m_imag);
p.m_imag = (m_real * arg_c.m_imag) + (m_imag * arg_c.m_real);
return p;
}
// divide function
Complex operator/(const Complex &arg_c) const
{
Complex p;
p.m_real = (arg_c.m_real * m_real + m_imag * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
p.m_imag = (arg_c.m_real * m_imag - m_real * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
return p;
}
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag == 0)
arg_os << arg_c.m_real;
else if (arg_c.m_imag > 0)
arg_os << arg_c.m_real << " + " << arg_c.m_imag << 'i';
else
arg_os << arg_c.m_real << " - " << (-1) * (arg_c.m_imag) << 'i';
return arg_os;
}
friend istream &operator>>(istream &arg_is, Complex &arg_c)
{
string str_x, str_y, temp;
if (getline(arg_is, str_x, ' '))
{
if (getline(arg_is, str_y, '\n'))
{
arg_c.m_real = stod(str_x);
arg_c.m_imag = stod(str_y);
}
}
return arg_is;
}
friend class Complex_Calc;
};
// Complex calculator class declaration
class Complex_Calc
{
private:
// define current value
Complex m_curr_val;
// define input value
Complex m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and `=`
string m_op;
// calculate result
void _calc_result()
{
switch (m_op[0])
{
case '+':
_add();
break;
case '-':
_sub();
break;
case '*':
_mul();
break;
case '/':
_div();
break;
case '=':
_assign();
break;
}
return;
}
// operation functions
// add the input value to the current value
void _add()
{
m_curr_val += m_input_val;
return;
}
// subtract the input value from the current value
void _sub()
{
m_curr_val -= m_input_val;
return;
}
// multiply the input value with the current value
void _mul()
{
m_curr_val *= m_input_val;
return;
}
// divide the current value by the input value
void _div()
{
m_curr_val /= m_input_val;
return;
}
// assign the input value to the current value
void _assign()
{
m_curr_val = m_input_val;
return;
}
public:
// Constructor
Complex_Calc(const Complex &arg_curr_val = Complex(0, 0),
const Complex &arg_input_val = Complex(0, 0),
const string op = "=")
{
m_curr_val = arg_curr_val;
m_input_val = arg_input_val;
m_op = op;
}
//(const Complex &arg_curr_val = (0, 0),
// const Complex &arg_input_val = (0,0),
// const char op = '=')
// Copy constructor
Complex_Calc(const Complex_Calc &arg_int_calc)
{
m_curr_val = arg_int_calc.m_curr_val;
m_input_val = arg_int_calc.m_input_val;
m_op = arg_int_calc.m_op;
}
// Destructor
~Complex_Calc(){}; // no need to do anything
// set input value or operation
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc)
{
arg_os << arg_comp_calc.m_curr_val;
return arg_os;
}
};
// parse the test cases, do not modify belows
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
void Complex_Calc::set_input(const string &arg_input)
{
// input is empty, read again
if (arg_input.empty())
{
error_and_exit();
return;
}
// input is a operation
else if (arg_input == "+" || arg_input == "-"
|| arg_input == "*" || arg_input == "/" || arg_input == "=")
{
m_op = arg_input;
}
// input is a complex number
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
else
{
stringstream ss(arg_input);
ss >> m_input_val;
if (m_input_val.m_imag == 0 && m_input_val.m_real == 0 && m_op == "/")
{
error_and_exit();
}
_calc_result();
}
}
// main function
bool test(string input, int n)
{
if (n % 2 == 0)
{
int t = 0;
for (int i = 0; i < input.size(); i++)
{
if (input[i] == ' ')
{
t++;
}
}
if (t != 1)
{
return false;
}
double real, imag;
stringstream ss(input);
ss >> real;
if (ss.fail()) // if fail return false
{
return false;
}
ss >> imag;
if (ss.fail())
{
return false;
}
if (!ss.eof()) // if it is not the end of file return false
{
return false;
}
}
else
{
if (input.size() != 1)
{
return false;
}
else if (input[0] != '+' && input[0] != '-'
&& input[0] != '*' && input[0] != '/')
{
return false;
}
}
return true;
}
int main()
{
int n = 0;
// create an instance of the class
Complex_Calc calc;
string input;
while (getline(cin, input))
{
if (!(test(input, n)))
{
error_and_exit();
}
calc.set_input(input);
cout << calc << endl;
n++;
}
}
陳誼倫(110021127)
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Complex_Calc;
class Complex
{
private:
double m_real;
double m_imag;
public:
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
Complex(const Complex &arg_c);
Complex &operator=(const Complex &arg_c);
Complex &operator+=(const Complex &arg_c);
Complex &operator-=(const Complex &arg_c);
Complex &operator*=(const Complex &arg_c);
Complex &operator/=(const Complex &arg_c);
Complex operator+(const Complex &arg_c) const
{
Complex res(*this);
res += arg_c;
return res;
}
Complex operator-(const Complex &arg_c) const
{
Complex res(*this);
res -= arg_c;
return res;
}
Complex operator*(const Complex &arg_c) const
{
Complex res(*this);
res *= arg_c;
return res;
}
Complex operator/(const Complex &arg_c) const
{
Complex res(*this);
res /= arg_c;
return res;
}
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
friend istream &operator>>(istream &arg_is, Complex &arg_c);
friend class Complex_Calc;
};
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag) {}
Complex::Complex(const Complex &arg_point)
: m_real(arg_point.m_real), m_imag(arg_point.m_imag) {}
Complex &Complex::operator=(const Complex &arg_c)
{
this->m_real = arg_c.m_real;
this->m_imag = arg_c.m_imag;
return *this;
}
Complex &Complex::operator+=(const Complex &arg_c)
{
this->m_real += arg_c.m_real;
this->m_imag += arg_c.m_imag;
return *this;
}
Complex &Complex::operator-=(const Complex &arg_c)
{
this->m_real -= arg_c.m_real;
this->m_imag -= arg_c.m_imag;
return *this;
}
Complex &Complex::operator*=(const Complex &arg_c)
{
double _real = this->m_real, _imag = this->m_imag;
this->m_real = (_real * arg_c.m_real) - (_imag * arg_c.m_imag);
this->m_imag = (_real * arg_c.m_imag) + (_imag * arg_c.m_real);
return *this;
}
Complex &Complex::operator/=(const Complex &arg_c)
{
double _real = this->m_real, _imag = this->m_imag;
this->m_real = ((_real * arg_c.m_real) + (_imag * arg_c.m_imag))
/ ((arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag));
this->m_imag = ((-_real * arg_c.m_imag) + (_imag * arg_c.m_real))
/ ((arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag));
return *this;
}
std::ostream &operator<<(std::ostream &arg_os, const Complex &arg_point)
{
if (arg_point.m_imag == 0)
{
arg_os << arg_point.m_real;
return arg_os;
}
else if (arg_point.m_imag < 0)
{
arg_os << arg_point.m_real << " - " << -arg_point.m_imag << "i ";
return arg_os;
}
else
{
arg_os << arg_point.m_real << " + " << arg_point.m_imag << "i ";
return arg_os;
}
}
std::istream &operator>>(std::istream &arg_is, Complex &arg_point)
{
string str_x, str_y, temp;
if (getline(arg_is, str_x, ' '))
{
if (getline(arg_is, str_y, ' '))
{
arg_point.m_real = stod(str_x);
arg_point.m_imag = stod(str_y);
}
}
return arg_is;
}
class Complex_Calc
{
private:
Complex m_curr_val;
Complex m_input_val;
char m_op, op;
int process = 0;
void _calc_result()
{
switch (m_op)
{
case '+':
m_curr_val += m_input_val;
break;
case '-':
m_curr_val -= m_input_val;
break;
case '*':
m_curr_val *= m_input_val;
break;
case '/':
if (m_input_val.m_real == 0 && m_input_val.m_imag == 0)
{
error_and_exit();
}
else
{
m_curr_val /= m_input_val;
break;
}
case '=':
m_curr_val = m_input_val;
break;
}
}
void _add()
{
m_op = '+';
}
void _sub()
{
m_op = '-';
}
void _mul()
{
m_op = '*';
}
void _div()
{
m_op = '/';
}
void _assign()
{
m_op = '=';
}
public:
Complex_Calc();
Complex_Calc(const Complex_Calc &arg_int_calc);
~Complex_Calc(){};
void error_and_exit();
void set_input(const string &arg_input);
friend ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc);
};
Complex_Calc::Complex_Calc() : m_curr_val(), m_input_val(), m_op('=')
{
}
Complex_Calc::Complex_Calc(const Complex_Calc &arg_int_calc)
: m_curr_val(arg_int_calc.m_curr_val),
m_input_val(arg_int_calc.m_input_val),
m_op(arg_int_calc.m_op)
{
}
bool check_complex(const string &input)
{
string temp_str;
vector<string> vec;
stringstream terms_extractor(input);
while (terms_extractor >> temp_str)
{
vec.push_back(temp_str);
}
if (vec.size() == 2)
{
if ((!isdigit(vec[0][0]) && vec[0][0] != '-')
|| (!isdigit(vec[1][0]) && vec[1][0] != '-'))
{
return false;
}
for (int i = 1; i < vec[0].size(); i++)
{
if (isdigit(vec[0][i]) || vec[0][i] == '.')
{
continue;
}
else
{
return false;
}
}
for (int i = 1; i < vec[1].size(); i++)
{
if (isdigit(vec[1][i]) || vec[1][i] == '.')
{
continue;
}
else
{
return false;
}
}
}
else
{
return false;
}
return true;
}
bool check_op(const string &input)
{
if (input == "+" || input == "-" || input == "*" || input == "/")
{
return true;
}
else
{
return false;
}
}
void Complex_Calc::set_input(const string &arg_input)
{
if ((process % 2 == 1) && (check_op(arg_input) == true))
{
op = arg_input[0];
}
else if ((process % 2 == 0) && (check_complex(arg_input) == true))
{
switch (op)
{
case '+':
_add();
break;
case '-':
_sub();
break;
case '*':
_mul();
break;
case '/':
_div();
break;
case '=':
_assign();
break;
}
stringstream ss(arg_input);
ss >> m_input_val;
_calc_result();
}
else
{
error_and_exit();
}
process = process + 1;
}
void Complex_Calc::error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
std::ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc)
{
arg_os << arg_comp_calc.m_curr_val;
return arg_os;
}
// main function
int main()
{
// create an instance of the class
Complex_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
TA
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
using namespace std;
class Complex_Calc;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// subtract assignment operator
Complex &operator-=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// divide assignment operator
Complex &operator/=(const Complex &arg_c);
// add function
Complex operator+(const Complex &arg_c) const;
// subtract function
Complex operator-(const Complex &arg_c) const;
// multiply function
Complex operator*(const Complex &arg_c) const;
// divide function
Complex operator/(const Complex &arg_c) const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
friend class Complex_Calc;
};
// Complex calculator class declaration
class Complex_Calc
{
private:
// define current value
Complex m_curr_val;
// define input value
Complex m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and `=`
char m_op;
// define input status, turns `op` for true and turns `value` for false
bool m_op_input;
// calculate result
void _calc_result();
// operation functions
// set activation op to add
void _add();
// set activation op to subtract
void _sub();
// set activation op to multiply
void _mul();
// set activation op to divide
void _div();
// set activation op to assign
void _assign();
public:
// Constructor
Complex_Calc();
// Copy constructor
Complex_Calc(const Complex_Calc &arg_int_calc);
// Destructor
~Complex_Calc(){}; // no need to do anything
// set input value or operation
// as the same as the user input number or operation
// into the calculator
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc);
};
// error and exit
void error_and_exit()
{
cerr << "Error: Invalid input" << endl;
exit(1);
}
// Complex class implementation
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
// Copy constructor
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
// assignment operator
Complex &Complex::operator=(const Complex &arg_c)
{
if (this == &arg_c) // self-assignment
return *this;
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
// add assignment operator
Complex &Complex::operator+=(const Complex &arg_c)
{
m_real += arg_c.m_real;
m_imag += arg_c.m_imag;
return *this;
}
// subtract assignment operator
Complex &Complex::operator-=(const Complex &arg_c)
{
m_real -= arg_c.m_real;
m_imag -= arg_c.m_imag;
return *this;
}
// multiply assignment operator
Complex &Complex::operator*=(const Complex &arg_c)
{
double real = m_real * arg_c.m_real - m_imag * arg_c.m_imag;
double imag = m_real * arg_c.m_imag + m_imag * arg_c.m_real;
m_real = real;
m_imag = imag;
return *this;
}
// divide assignment operator
Complex &Complex::operator/=(const Complex &arg_c)
{
if (arg_c.m_real == 0 && arg_c.m_imag == 0)
error_and_exit();
double real = (m_real * arg_c.m_real + m_imag * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
double imag = (m_imag * arg_c.m_real - m_real * arg_c.m_imag)
/ (arg_c.m_real * arg_c.m_real + arg_c.m_imag * arg_c.m_imag);
m_real = real;
m_imag = imag;
return *this;
}
// add function
Complex Complex::operator+(const Complex &arg_c) const
{
Complex c(*this);
c += arg_c;
return c;
}
// subtract function
Complex Complex::operator-(const Complex &arg_c) const
{
Complex c(*this);
c -= arg_c;
return c;
}
// multiply function
Complex Complex::operator*(const Complex &arg_c) const
{
Complex c(*this);
c *= arg_c;
return c;
}
// divide function
Complex Complex::operator/(const Complex &arg_c) const
{
Complex c(*this);
c /= arg_c;
return c;
}
// cout `<<` operator for print complex number
// note: be careful about the format of output
ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag > 0)
{
arg_os << arg_c.m_real << " + " << arg_c.m_imag << "i";
}
else if (arg_c.m_imag < 0)
{
arg_os << arg_c.m_real << " - " << -arg_c.m_imag << "i";
}
else
{
arg_os << arg_c.m_real;
}
return arg_os;
}
// cin `>>` operator for input complex number
// note: be careful about the format of input
istream &operator>>(istream &arg_is, Complex &arg_c)
{
double input_real, input_imag;
arg_is >> input_real;
if (arg_is.fail())
{
error_and_exit();
}
arg_is >> input_imag;
if (arg_is.fail() || !arg_is.eof())
{
error_and_exit();
}
arg_c.m_real = input_real;
arg_c.m_imag = input_imag;
return arg_is;
}
// Complex_Calc class implementation
// Constructor
Complex_Calc::Complex_Calc()
: m_curr_val(), m_input_val(), m_op('='), m_op_input(false)
{
}
// Copy constructor
Complex_Calc::Complex_Calc(const Complex_Calc &arg_int_calc)
: m_curr_val(arg_int_calc.m_curr_val),
m_input_val(arg_int_calc.m_input_val),
m_op(arg_int_calc.m_op),
m_op_input(arg_int_calc.m_op_input)
{
}
void Complex_Calc::set_input(const string &arg_input)
{
// input is empty, read again
if (arg_input.empty())
return;
// input is a operator in right turn
else if (m_op_input && (arg_input == "+" || arg_input == "-"
|| arg_input == "*" || arg_input == "/" || arg_input == "="))
{
// set the activated operation
// as the same as the user press the op button
switch (arg_input[0])
{
case '+':
_add();
break;
case '-':
_sub();
break;
case '*':
_mul();
break;
case '/':
_div();
break;
case '=':
_assign();
break;
}
// set to 'input a complex number' turn
m_op_input = false;
}
// input is a complex number in right turn
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
else if (!m_op_input)
{
stringstream ss(arg_input);
ss >> m_input_val;
_calc_result();
m_op_input = true;
}
// else, input is invalid
else
{
error_and_exit();
}
}
void Complex_Calc::_calc_result()
{
switch (m_op)
{
case '+':
m_curr_val += m_input_val;
break;
case '-':
m_curr_val -= m_input_val;
break;
case '*':
m_curr_val *= m_input_val;
break;
case '/':
m_curr_val /= m_input_val;
break;
case '=':
m_curr_val = m_input_val;
break;
}
}
// add the input value to the current value
void Complex_Calc::_add()
{
m_op = '+';
}
// subtract the input value from the current value
void Complex_Calc::_sub()
{
m_op = '-';
}
// multiply the input value with the current value
void Complex_Calc::_mul()
{
m_op = '*';
}
// divide the current value by the input value
void Complex_Calc::_div()
{
m_op = '/';
}
// assign the input value to the current value
void Complex_Calc::_assign()
{
m_op = '=';
}
// cout `<<` operator for print calculator status
ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc)
{
arg_os << arg_comp_calc.m_curr_val;
return arg_os;
}
// main function
int main()
{
// create an instance of the class
Complex_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
Introduction to Object Oriented Programming & Design
Slides version: lecture7_slides.html Website version: lecture7.html
- What is Object Oriented Programming?
- What is Object Oriented Analysis and Design?
- Object Oriented Analysis
- Example: Calculator
- Use cases
- Object models
- Example: Calculator
- Object Oriented Design
- Example: Calculator
- System Design
- Object Design
- Example: Calculator
- Object Oriented Implementation
- Example: Calculator
- Summary
- Pratices
What is Object Oriented Programming?
Example: Calculator
| C | ± | % | / |
| 7 | 8 | 9 | * |
| 4 | 5 | 6 | - |
| 1 | 2 | 3 | + |
| 0 | . | = |
A calculator consists of a set of buttons, each of which has following functions:
- Numbers:
1,2,3,4,5,6,7,8,9,0 - Operations:
+,-,*,/ - Symbols: ±(
plusminus),%,. - Function:
=,C(lear)
So, we can model the calculator as a class. For example:
class Button
{
// ...
};
class Calc_Controller
{
// ...
};
class Calculator
{
// ...
};
But, how?
What is Object Oriented Analysis and Design?
Object-oriented analysis and design - Wikipedia
Object-oriented analysis and design (OOAD) is a technical approach for analyzing and designing an application, system, or business by applying object-oriented programming, as well as using visual modeling throughout the software development process to guide stakeholder communication and product quality.
Object Oriented Analysis
First, we need to review the use cases and list the object models.
Use case: Calculator
- A calculator consists of a set of buttons, each of which has following functions:
- Numbers:
1,2,3,4,5,6,7,8,9,0 - Operations:
+,-,*,/ - Symbols: ±(
plusminus),%,. - Function:
=,C(lear)
- Numbers:
- User want to type in a number, user need to press number buttons or
., from left to right- If the number is a percentage, press
%after finish typing a number - If the number is a negative number, press
±after finish typing a number - If the typed number is wrong, press
Cto clear the number
- If the number is a percentage, press
- After finish typing a number, user need to press an operation button
- perform the previous operation with the current result and the typed number
- If the typed number is the first number, set the result with the typed number, as the same as the user press
=in 2.
- If the typed number is the first number, set the result with the typed number, as the same as the user press
- Do 1. to 3. until user press
=
Object models: Calculator
Next, we need to list the objects and their attributes.
Calculator:
- result: number
- buttons:
- Numbers:
1,2,3,4,5,6,7,8,9,0 - Operations:
+,-,*,/ - Symbols: ±(
plusminus),%,. - Function:
=,C(lear)
- Numbers:
- controller
- a button is pressed
- a number is typed
Clear is pressed±is pressed%is pressed.is pressed
- an operation is pressed
=is pressed
Object Oriented Design
After we have the object models, we can design the system and the objects.
System Design
Calculator:
- input: buttons
- output: result
- status: result, controller, buttons
Use cases:
- send which button is pressed to controller
- send result to controller as the input of previous operation
- contoller will update the result of the calculator with the input number, operation, and the previous result
Object Design
Botton:
- identify which button is pressed
- send which button is pressed
Controller
- translate the pressed buttons to the corresponding actions:
- a number is typed
Clear is pressed±is pressed%is pressed
- an operation is pressed
=is pressed
- a number is typed
- get the previous result
- send the result to the calculator
Object Oriented Implementation
Finally, we can implement the system and the objects.
Botton
class Button
{
protected:
char symbol;
public:
Button(char arg_btn_char)
: symbol(arg_btn_char)
{
}
virtual char press() const // polymorphism, will discuss in lecture 11
{
return '\0';
}
};
class Num_Button : public Button // inherits from Button, will discuss in next lecture
{
public:
Num_Button(char arg_btn_char = '\0') : Button(arg_btn_char)
{
// ...
}
char press() const
{
return symbol;
}
};
class Op_Button : public Button
{
public:
Op_Button(char arg_btn_char = '\0') : Button(arg_btn_char)
{
// ...
}
char press() const
{
return symbol;
}
};
class Sym_Button : public Button
{
public:
Sym_Button(char arg_btn_char = '\0') : Button(arg_btn_char)
{
// ...
}
char press() const
{
return symbol;
}
};
class Func_button : public Button
{
public:
Func_button(char arg_btn_char = '\0') : Button(arg_btn_char)
{
// ...
}
char press() const
{
return symbol;
}
};
Controller
class Calc_Controller
{
private:
int status; // 0 = init, 1 = type num, 2 = press op or assign
char next_op;
char curr_op;
bool decimal_pressed;
double type_num;
bool minus_pressed;
int decimal_offset;
public:
Calc_Controller()
: status(0), next_op('='), curr_op('='), decimal_pressed(false),
type_num(0), minus_pressed(false), decimal_offset(1)
{
}
void button_pressed(Button &arg_btn)
{
switch (status)
{
case 0:
if (typeid(arg_btn) == typeid(Num_Button))
{
status = 1;
type_num = arg_btn.press() - '0';
}
else if (typeid(arg_btn) == typeid(Op_Button))
{
status = 2;
next_op = arg_btn.press();
}
else if (typeid(arg_btn) == typeid(Sym_Button))
{
status = 1;
switch (arg_btn.press())
{
case '.':
decimal_pressed = true;
break;
case 'p':
minus_pressed = true;
break;
default:
break;
}
}
else if (typeid(arg_btn) == typeid(Func_button))
{
status = 0;
next_op = '=';
arg_btn.press();
}
break;
case 1:
if (typeid(arg_btn) == typeid(Num_Button))
{
if (decimal_pressed)
{
decimal_offset *= 10;
}
type_num *= 10;
type_num += arg_btn.press() - '0';
}
else if (typeid(arg_btn) == typeid(Op_Button))
{
status = 2;
curr_op = next_op;
next_op = arg_btn.press();
type_num = type_num * (minus_pressed ? -1 : 1) / decimal_offset;
}
else if (typeid(arg_btn) == typeid(Sym_Button))
{
switch (arg_btn.press())
{
case '.':
decimal_pressed = true;
break;
case 'p':
minus_pressed = !minus_pressed;
break;
case '%':
type_num = type_num * 0.01;
break;
default:
break;
}
}
else if (typeid(arg_btn) == typeid(Func_button))
{
switch (arg_btn.press())
{
case 'c':
type_num = 0;
break;
case '=':
curr_op = next_op;
next_op = arg_btn.press();
status = 2;
type_num = type_num * (minus_pressed ? -1 : 1) / decimal_offset;
}
}
break;
case 2:
if (typeid(arg_btn) == typeid(Num_Button))
{
status = 1;
type_num = arg_btn.press() - '0';
}
else if (typeid(arg_btn) == typeid(Op_Button))
{
next_op = arg_btn.press();
}
else if (typeid(arg_btn) == typeid(Sym_Button))
{
status = 1;
switch (arg_btn.press())
{
case '.':
decimal_pressed = true;
break;
case 'p':
minus_pressed = !minus_pressed;
break;
case '%':
type_num = type_num * 0.01;
break;
default:
break;
}
}
else if (typeid(arg_btn) == typeid(Func_button))
{
switch (arg_btn.press())
{
case 'c':
type_num = 0;
status = 0;
curr_op = '=';
next_op = '=';
break;
case '=':
curr_op = '=';
next_op = '=';
break;
}
}
break;
}
}
double update_result(const double &arg_result)
{
switch (status)
{
case 0:
return arg_result;
case 1:
return arg_result;
case 2:
switch (curr_op)
{
case '+':
return arg_result + type_num;
case '-':
return arg_result - type_num;
case '*':
return arg_result * type_num;
case '/':
return arg_result / type_num;
case '=':
return type_num;
default:
return arg_result;
}
}
return arg_result;
}
};
Calculator
class Calculator
{
private:
double result;
Calc_Controller controller;
Num_Button num_buttons[10];
Op_Button op_buttons[4];
Sym_Button sym_buttons[3];
Func_button func_buttons[2];
void _run()
{
controller.button_pressed(num_buttons[1]); // 1
result = controller.update_result(result);
controller.button_pressed(op_buttons[0]); // +
result = controller.update_result(result);
controller.button_pressed(num_buttons[2]); // 2
result = controller.update_result(result);
controller.button_pressed(func_buttons[1]); // =
result = controller.update_result(result);
}
public:
Calculator() // like we turn on a calculator
: result(0.0), controller()
{
// init num_buttons
for (int i = 0; i < 10; i++)
{
num_buttons[i] = Num_Button(i + '0');
}
// init op_buttons
op_buttons[0] = Op_Button('+');
op_buttons[1] = Op_Button('-');
op_buttons[2] = Op_Button('*');
op_buttons[3] = Op_Button('/');
// init sym_buttons
sym_buttons[0] = Sym_Button('.');
sym_buttons[1] = Sym_Button('p');
sym_buttons[2] = Sym_Button('%');
// init func_buttons
func_buttons[0] = Func_button('C');
func_buttons[1] = Func_button('=');
_run();
}
~Calculator() // like we turn off a calculator
{
}
};
int main()
{
Calculator calc;
return 0;
}
Summary
4 steps to perform object-oriented programming:
- Define use cases
- Define objects by use cases
- Define whole system by objects
- Detail define objects and their properties
- Implement objects and system
Pratices
Use the workflow above to implement the following problems:
- Elevator system
- Basketball game
- Closet
OOP: Inheritance (1)
Slides version: lecture8_slides.html Website version: lecture8.html
- What is Inheritance? and Why do we need it?
- Example: Bus, Car, and Truck.
- Syntax
- Inheritance Mode
- Public, Protected, Private
- Example
- Public, Protected, Private
- Inheritance Type
- Single
- Multiple
- Multi-level
- Hierarchical (discuss in the next lecture)
- Hybrid (Virtual) Inheritance (discuss in the next lecture)
- Multipath inheritance (discuss in the next lecture)
- Example 1: Integer & Real
- Example 2: Complex Number
- Example 3: Integer & Real & Complex Number
- Pratices
What is Inheritance? and Why do we need it?
Ref: Inheritance in C++
The capability of a class to derive properties and characteristics from another class is called Inheritance.
Example: Bus, Car, and Truck.
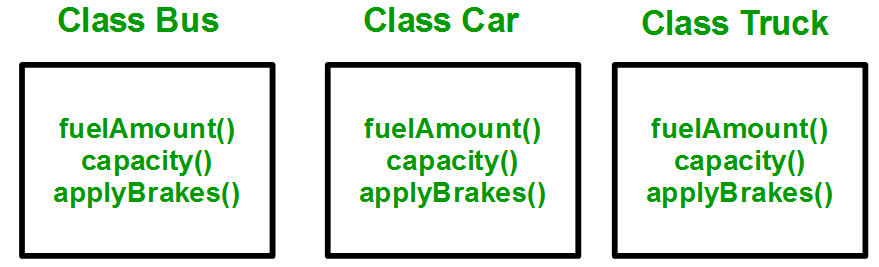
Because bus, car and truck are all vehicles, and they all have the same member functions, we can use inheritance to reduce the amount of code we need to write. For example, class Vehicle:
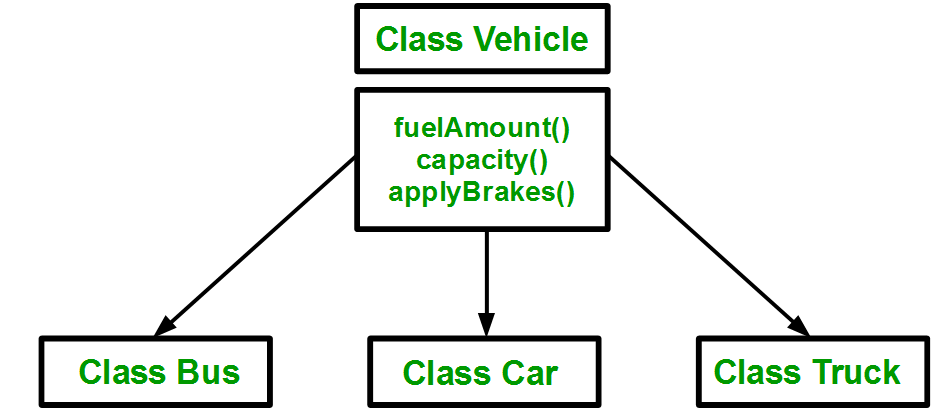
Syntax
class subclass_name : access_mode base_class_name
{
// body of subclass
};
Example: Bus, Car, and Truck.
#include <iostream>
using namespace std;
class Vehicle
{
public:
void run()
{
std::cout << "Vehicle is running" << std::endl;
}
};
class Bus : public Vehicle
{
};
class Car : public Vehicle
{
};
class Truck : public Vehicle
{
};
int main()
{
Bus bus;
Car car;
Truck truck;
bus.run();
car.run();
truck.run();
return 0;
}
Output:
$ ./a.out
Vehicle is running
Vehicle is running
Vehicle is running
Example: Parent & Child
// C++ program to demonstrate implementation
// of Inheritance
#include <bits/stdc++.h>
using namespace std;
// Base class
class Parent
{
public:
int id_p;
};
// Sub class inheriting from Base Class(Parent)
class Child : public Parent
{
public:
int id_c;
};
// main function
int main()
{
Child obj1;
// An object of class child has all data members
// and member functions of class parent
obj1.id_c = 7;
obj1.id_p = 91;
cout << "Child id is: " << obj1.id_c << '\n';
cout << "Parent id is: " << obj1.id_p << '\n';
return 0;
}
Output:
$ ./a.out
Child id is: 7
Parent id is: 91
Inheritance Mode
| Class Member Type | Type of | Inheritence | |
|---|---|---|---|
| Public | Protected | Private | |
| Public | Public | Protected | Private |
| Protected | Protected | Protected | Private |
| Private | Not accessible | Not accessible | Not accessible |
Example: Inheritance Mode
// C++ Implementation to show that a derived class
// doesn’t inherit access to private data members.
// However, it does inherit a full parent object.
class A
{
public:
int x;
protected:
int y;
private:
int z;
};
class B : public A
{
// x is public
// y is protected
// z is not accessible from B
};
class C : protected A
{
// x is protected
// y is protected
// z is not accessible from C
};
class D : private A // 'private' is default for classes
{
// x is private
// y is private
// z is not accessible from D
};
Inheritance Type
- Single
- Multiple
- Multi-level
- Hierarchical (discuss in the next lecture)
- Hybrid (Virtual) Inheritance (discuss in the next lecture)
- Multipath inheritance (discuss in the next lecture)
Single Inheritance
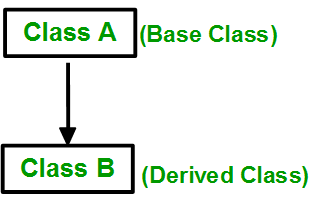
Syntax:
class subclass_name : access_mode base_class
{
// body of subclass
};
Example: Single Inheritance

// C++ program to explain
// Single inheritance
#include <iostream>
using namespace std;
// base class
class Vehicle
{
public:
Vehicle()
{
cout << "This is a Vehicle\n";
}
};
// sub class derived from a single base classes
class Car : public Vehicle
{
};
// main function
int main()
{
// Creating object of sub class will
// invoke the constructor of base classes
Car obj;
return 0;
}
Multiple Inheritance
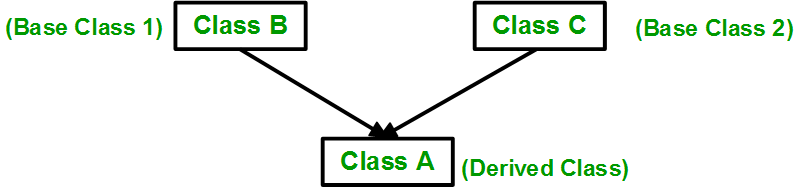
Syntax:
class subclass_name : access_mode base_class1,
access_mode base_class2,
....
{
// body of subclass
};
Example: Multiple Inheritance

// C++ program to explain
// multiple inheritance
#include <iostream>
using namespace std;
// first base class
class Vehicle
{
public:
Vehicle()
{
cout << "This is a Vehicle\n";
}
};
// second base class
class FourWheeler
{
public:
FourWheeler()
{
cout << "This is a 4 wheeler Vehicle\n";
}
};
// sub class derived from two base classes
class Car : public Vehicle, public FourWheeler
{
};
// main function
int main()
{
// Creating object of sub class will
// invoke the constructor of base classes.
Car obj;
return 0;
}
Multi-level Inheritance
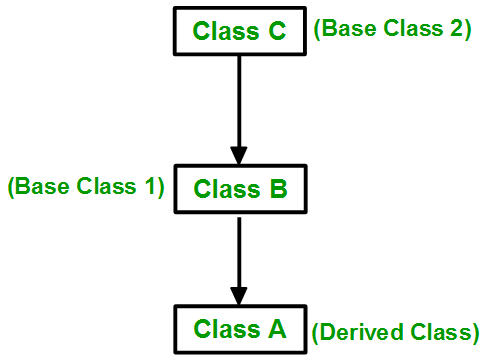
Syntax:
class base_class_1 : access_mode base_class_2
{
// body of base class 1
};
class subclass_name : access_mode base_class_1
{
// body of subclass
};
Example: Multi-level Inheritance

// C++ program to implement
// Multilevel Inheritance
#include <iostream>
using namespace std;
// base class
class Vehicle
{
public:
Vehicle()
{
cout << "This is a Vehicle\n";
}
};
// first sub_class derived from class vehicle
class fourWheeler : public Vehicle
{
public:
fourWheeler()
{
cout << "Objects with 4 wheels are vehicles\n";
}
};
// sub class derived from the derived base class fourWheeler
class Car : public fourWheeler
{
public:
Car()
{
cout << "Car has 4 Wheels\n";
}
};
// main function
int main()
{
// Creating object of sub class will
// invoke the constructor of base classes.
Car obj;
return 0;
}
Example 1: Integer & Real [Source]
Example 2: Complex Number [Source]
Example 3: Integer & Real & Complex Number [Source]
Pratices
- Design a class hierarchy for Fruit. Contains:
- Grape
- Apple
- Orange
- Design a class hierarchy for Quadrilateral. Contains:
- Square
- Rectangle
- Rhombus
- Parallelogram
Example 1: Integer & Real
#include <iostream>
using namespace std;
class Integer
{
private:
int m_int_value;
public:
Integer(int arg_int_value)
{
m_int_value = arg_int_value;
}
int get_int_value()
{
return m_int_value;
}
void set_int_value(int arg_int_value)
{
m_int_value = arg_int_value;
}
};
class Real : public Integer
{
private:
double after_decimal;
public:
Real(double arg_value) : Integer((int)arg_value),
after_decimal(arg_value - (int)arg_value)
{
}
double get_real_value()
{
return after_decimal + get_int_value();
}
void set_real_value(double arg_value)
{
set_int_value((int)arg_value);
after_decimal = arg_value - (int)arg_value;
}
};
int main()
{
Real r(3.14);
cout << r.get_int_value() << endl;
cout << r.get_real_value() << endl;
r.set_real_value(3.1415);
cout << r.get_real_value() << endl;
r.set_int_value(4);
cout << r.get_real_value() << endl;
return 0;
}
Example 2: Complex Number
#include <iostream>
using namespace std;
class Integer
{
private:
int m_int_value;
public:
Integer(int arg_int_value)
{
m_int_value = arg_int_value;
}
int get_int_value()
{
return m_int_value;
}
void set_int_value(int arg_int_value)
{
m_int_value = arg_int_value;
}
};
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
double get_real_value()
{
return m_after_decimal + get_int_value();
}
void set_real_value(double arg_value)
{
set_int_value((int)arg_value);
m_after_decimal = arg_value - (int)arg_value;
}
};
class Complex : protected Real
{
private:
Real m_imaginary;
public:
Complex(double arg_real_value,
double arg_imaginary_value)
: Real(arg_real_value),
m_imaginary(arg_imaginary_value)
{
}
double get_real_value()
{
return m_after_decimal + get_int_value();
}
double get_imaginary_value()
{
return m_imaginary.get_real_value();
}
void set_real_value(double arg_real_value)
{
Real::set_real_value(arg_real_value);
}
void set_imaginary_value(double arg_imaginary_value)
{
m_imaginary.set_real_value(arg_imaginary_value);
}
};
int main()
{
Complex c(1.5, 2.5);
cout << c.get_real_value() << " + "
<< c.get_imaginary_value() << "i" << endl;
c.set_real_value(3.5);
c.set_imaginary_value(4.5);
cout << c.get_real_value()
<< " + " << c.get_imaginary_value() << "i" << endl;
return 0;
}
Example 3: Integer & Real & Complex Number
#include <iostream>
using namespace std;
class Integer
{
private:
int m_int_value;
public:
Integer(int arg_int_value)
{
m_int_value = arg_int_value;
}
int get_int_value()
{
return m_int_value;
}
void set_int_value(int arg_int_value)
{
m_int_value = arg_int_value;
}
};
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
double get_real_value()
{
return m_after_decimal + get_int_value();
}
void set_real_value(double arg_value)
{
set_int_value((int)arg_value);
m_after_decimal = arg_value - (int)arg_value;
}
};
class Imaginary
{
protected:
double m_imaginary_value;
public:
Imaginary(double arg_imaginary_value)
{
m_imaginary_value = arg_imaginary_value;
}
double get_imaginary_value()
{
return m_imaginary_value;
}
void set_imaginary_value(double arg_imaginary_value)
{
m_imaginary_value = arg_imaginary_value;
}
};
class Complex : public Real, public Imaginary
{
public:
Complex(double arg_real_value,
double arg_imaginary_value)
: Real(arg_real_value),
Imaginary(arg_imaginary_value)
{
}
void print_complex_value()
{
cout << get_real_value() << " + " << m_imaginary_value << "i" << endl;
}
};
int main()
{
Complex c(1.5, 2.5);
c.print_complex_value();
c.set_real_value(3.5);
c.set_imaginary_value(4.5);
c.print_complex_value();
return 0;
}
Midterm Project: Big Positive Real Number Calculator
Midterm-1: Big Positive Real Number in Decimal Point Format (40%)
-
Inputs:
- Input a big positive real number in decimal point format, one line for one number.
- digits before and after the decimal point are at most 9 digits, separated by a point character
..
- digits before and after the decimal point are at most 9 digits, separated by a point character
- Input a operator, one line for one operator:
+: add*: multiply
- The input is interleaved, one line for one number and one line for one operator after the number.
- Input Ctrl+D to finish the input.
- Windows: Ctrl+Z (will show
^Zon the screen) then Enter (⏎in Format) to finish the input.
- Windows: Ctrl+Z (will show
- Input a big positive real number in decimal point format, one line for one number.
-
Outputs:
- The calculation result
- The result is shown in decimal point format, with at most 18 digits before the decimal point, and 9 digits after the decimal point (rounding toward zero, truncate).
- The format please refer to the Format section.
- The calculation result
-
File name:
midterm-1_<student_id>.cpp(e.g.midterm-1_106062802.cpp) -
The program will not have any user prompts, only print the result.
-
The program does not need to handle invalid inputs.
-
The program should be finished within 10 seconds. Any test cases will garuntee the program is finished within 10 seconds.
Format
<before dec 1>.<after dec 1>⏎
<op 1>⏎
<before dec 2>.<after dec 2>⏎
<op 2>⏎
...
<before dec n-1>.<after dec n-1>⏎
<op n-1>⏎
<before dec n>.<after dec n>⏎
^Z⏎
<before dec result>.<after dec result>
Example
$ ./a.out
1.0⏎
^Z⏎
1.000000000
$ ./a.out
0.2⏎
^Z⏎
0.200000000
$ ./a.out
1.0⏎
+⏎
2.0⏎
+
3.0⏎
*⏎
4.3⏎
^Z⏎
25.800000000
$ ./a.out
1.000000001⏎
+⏎
2.000000002⏎
^Z⏎
3.000000003
$ ./a.out
123456789.123456789⏎
+⏎
987654321.987654321⏎
^Z⏎
1111111111.111111110
$ ./a.out
1.000000001⏎
*⏎
2.000000002⏎
^Z⏎
2.000000004
$ ./a.out
123456789.123456789⏎
*⏎
987654321.987654321⏎
^Z⏎
121932631356500531.347203169
Reference
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <iomanip>
using namespace std;
class BigReal
{
private:
// data members
// save the digits before and after the decimal point of a before_decimal number
// with `long long` precision
const long long m_dec_upperbound = 1000000000;
long long m_before_decimal;
long long m_after_decimal; // times 10^-9
void _output_normalization();
public:
// Constructor, initializes before_decimal and after_decimalinary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
BigReal(const long long &arg_before_decimal = 0.0,
const long long &arg_after_decimal = 0.0);
// Copy constructor
BigReal(const BigReal &arg_big_real);
// assignment operator
BigReal &operator=(const BigReal &arg_big_real);
// add assignment operator
BigReal &operator+=(const BigReal &arg_big_real);
// multiply assignment operator
BigReal &operator*=(const BigReal &arg_big_real);
// add function
BigReal operator+(const BigReal &arg_big_real) const;
// multiply function
BigReal operator*(const BigReal &arg_big_real) const;
// cout `<<` operator for print BigReal number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal &arg_big_real);
// cin `>>` operator for input BigReal number
// note: be careful about the format of input
// hint: use string `+=` to append digits
friend istream &operator>>(istream &arg_is, BigReal &arg_big_real);
};
int main()
{
string input;
BigReal result_complex;
char op = '=';
while (getline(cin, input))
{
// input is a operation
if (input == "+" || input == "*")
{
op = input[0];
continue;
}
else if (input.empty())
{
continue;
}
// input is a BigReal number
else
{
stringstream ss(input);
BigReal current_complex;
ss >> current_complex;
switch (op)
{
case '+':
result_complex += current_complex;
break;
case '*':
result_complex *= current_complex;
break;
case '=':
result_complex = current_complex;
break;
default:
cerr << "Error: unknown operation" << endl;
return 1;
}
}
}
cout << endl;
cout << result_complex << endl;
return 0;
}
TA Version Code
#include <iostream>
#include <string>
#include <sstream>
#include <iomanip>
using namespace std;
class BigReal
{
private:
// data members
// save the digits before and after the decimal point of a before_decimal number
// with `long long` precision
const long long m_dec_upperbound = 1000000000;
long long m_before_decimal;
long long m_after_decimal; // times 10^-9
void _output_normalization()
{
if (m_after_decimal < 0)
{
m_before_decimal -= 1;
m_after_decimal += m_dec_upperbound;
}
if (m_after_decimal > m_dec_upperbound)
{
m_before_decimal += m_after_decimal / m_dec_upperbound;
m_after_decimal = m_after_decimal % m_dec_upperbound;
}
}
public:
// Constructor, initializes before_decimal and after_decimalinary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
BigReal(const long long &arg_before_decimal = 0.0,
const long long &arg_after_decimal = 0.0)
: m_before_decimal(arg_before_decimal), m_after_decimal(arg_after_decimal)
{
}
// Copy constructor
BigReal(const BigReal &arg_big_real)
: m_before_decimal(arg_big_real.m_before_decimal),
m_after_decimal(arg_big_real.m_after_decimal)
{
}
// assignment operator
BigReal &operator=(const BigReal &arg_big_real)
{
if (this == &arg_big_real) // self-assignment
return *this;
m_before_decimal = arg_big_real.m_before_decimal;
m_after_decimal = arg_big_real.m_after_decimal;
return *this;
}
// add assignment operator
BigReal &operator+=(const BigReal &arg_big_real)
{
m_before_decimal += arg_big_real.m_before_decimal;
m_after_decimal += arg_big_real.m_after_decimal;
_output_normalization();
return *this;
}
// multiply assignment operator
BigReal &operator*=(const BigReal &arg_big_real)
{
long long before_decimal = m_before_decimal * arg_big_real.m_before_decimal;
long long after_decimal = m_after_decimal * arg_big_real.m_after_decimal / m_dec_upperbound;
after_decimal += m_before_decimal * arg_big_real.m_after_decimal;
after_decimal += m_after_decimal * arg_big_real.m_before_decimal;
m_before_decimal = before_decimal;
m_after_decimal = after_decimal;
_output_normalization();
return *this;
}
// add function
BigReal operator+(const BigReal &arg_big_real) const
{
BigReal c(*this);
c += arg_big_real;
return c;
}
// multiply function
BigReal operator*(const BigReal &arg_big_real) const
{
BigReal c(*this);
c *= arg_big_real;
return c;
}
// cout `<<` operator for print BigReal number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal &arg_big_real)
{
arg_os << arg_big_real.m_before_decimal << '.'
<< setfill('0') << setw(9) << arg_big_real.m_after_decimal;
return arg_os;
}
// cin `>>` operator for input BigReal number
// note: be careful about the format of input
// hint: use string `+=` to append digits
friend istream &operator>>(istream &arg_is, BigReal &arg_big_real)
{
string str_before_decimal, str_after_decimal;
getline(arg_is, str_before_decimal, '.');
getline(arg_is, str_after_decimal);
str_after_decimal = str_after_decimal.substr(0, 9);
for (int i = 0; i < 9; i++)
if (i >= str_after_decimal.size())
str_after_decimal += '0';
arg_big_real.m_before_decimal = stoll(str_before_decimal);
arg_big_real.m_after_decimal = stoll(str_after_decimal);
return arg_is;
}
};
int main()
{
string input;
BigReal result_complex;
char op = '=';
while (getline(cin, input))
{
// input is a operation
if (input == "+" || input == "*")
{
op = input[0];
continue;
}
else if (input.empty())
{
continue;
}
// input is a BigReal number
else
{
stringstream ss(input);
BigReal current_complex;
ss >> current_complex;
switch (op)
{
case '+':
result_complex += current_complex;
break;
case '*':
result_complex *= current_complex;
break;
case '=':
result_complex = current_complex;
break;
default:
cerr << "Error: unknown operation" << endl;
return 1;
}
}
}
cout << endl;
cout << result_complex << endl;
return 0;
}
Midterm-2: Simple Big Positive Real Number Calculator (40%)
-
Inputs:
- Input a big positive real number in decimal point format, one line for one number.
- digits before and after the decimal point are at most 9 digits, separated by a point character
..
- digits before and after the decimal point are at most 9 digits, separated by a point character
- Input a operator, one line for one operator:
+: add*: multiply
- The input is interleaved, one line for one number and one line for one operator after the number.
- Input Ctrl+D to finish the input.
- Windows: Ctrl+Z (will show
^Zon the screen) then Enter (⏎in Format) to finish the input.
- Windows: Ctrl+Z (will show
- Input a big positive real number in decimal point format, one line for one number.
-
Outputs:
- The calculation result
- The result is shown in decimal point format, with at most 18 digits before the decimal point, and 9 digits after the decimal point (rounding toward zero, truncate).
- If the input is an operator, the program should print the current result in the following line. The format please refer to the Example section.
- The calculation result
-
File name:
midterm-2_<student_id>.cpp(e.g.midterm-2_106062802.cpp) -
The program will not have any user prompts, only print the result.
-
The program does not need to handle invalid inputs.
-
Please use
mainandBigReal_Calc::set_inputthat provided in the pseudo code to handle the input and output. -
The program should be finished within 10 seconds. Any test cases will garuntee the program is finished within 10 seconds.
Format
<before dec 1>.<after dec 1>⏎
<result 1>
<op 1>⏎
<result 1>
<before dec 2>.<after dec 2>⏎
<result 2>
<op 2>⏎
<result 2>
...
<before dec n-1>.<after dec n-1>⏎
<result n-1>
<op n-1>⏎
<result n-1>
<before dec n>.<after dec n>⏎
<result n>
^Z⏎
Example
$ ./a.out
1.0⏎
1.000000000
^Z⏎
$ ./a.out
0.2⏎
0.200000000
^Z⏎
$ ./a.out
1.0⏎
1.000000000
+⏎
1.000000000
2.0⏎
3.000000000
+⏎
3.000000000
3.0⏎
6.000000000
*⏎
6.000000000
4.3⏎
25.800000000
^Z⏎
$ ./a.out
1.000000001⏎
1.000000001
+⏎
1.000000001
2.000000002⏎
3.000000003
^Z⏎
$ ./a.out
123456789.123456789⏎
123456789.123456789
+⏎
123456789.123456789
987654321.987654321⏎
1111111111.111111110
^Z⏎
$ ./a.out
1.000000001⏎
1.000000001
*⏎
1.000000001
2.000000002⏎
2.000000004
^Z⏎
$ ./a.out
123456789.123456789⏎
123456789.123456789
*⏎
123456789.123456789
987654321.987654321⏎
121932631356500531.347203169
^Z⏎
Reference
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <iomanip>
using namespace std;
class BigReal_Calc;
class BigReal
{
private:
// data members
// save the digits before and after the decimal point of a before_decimal number
// with `long long` precision
const long long m_dec_upperbound = 1000000000;
long long m_before_decimal;
long long m_after_decimal; // times 10^-9
void _output_normalization();
public:
// Constructor, initializes before_decimal and after_decimalinary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
BigReal(const long long &arg_before_decimal = 0.0,
const long long &arg_after_decimal = 0.0);
// Copy constructor
BigReal(const BigReal &arg_big_real);
// assignment operator
BigReal &operator=(const BigReal &arg_big_real);
// add assignment operator
BigReal &operator+=(const BigReal &arg_big_real);
// multiply assignment operator
BigReal &operator*=(const BigReal &arg_big_real);
// add function
BigReal operator+(const BigReal &arg_big_real) const;
// multiply function
BigReal operator*(const BigReal &arg_big_real) const;
// cout `<<` operator for print BigReal number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal &arg_big_real);
// cin `>>` operator for input BigReal number
// note: be careful about the format of input
// hint: use string `+=` to append digits
friend istream &operator>>(istream &arg_is, BigReal &arg_big_real);
};
// BigReal calculator class declaration
class BigReal_Calc
{
private:
// define current value
BigReal m_curr_val;
// define input value
BigReal m_input_val;
// define operation
// `+`, `*`, and `=`
char m_op;
// calculate result
void _calc_result();
// operation functions
// add the input value to the current value
void _add();
// subtract the input value from the current value
void _mul();
// divide the current value by the input value
void _assign();
public:
// Constructor
BigReal_Calc();
// Copy constructor
BigReal_Calc(const BigReal_Calc &arg_int_calc);
// Destructor
~BigReal_Calc(){}; // no need to do anything
// set input value or operation
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal_Calc &arg_comp_calc);
};
// parse the test cases, do not modify belows
void BigReal_Calc::set_input(const string &arg_input)
{
// input is empty, read again
if (arg_input.empty())
{
return;
}
// input is a operation
else if (arg_input == "+" || arg_input == "*" || arg_input == "=")
{
// set the activated operation
// as the same as the user press the op button
switch (arg_input[0])
{
case '+':
_add();
break;
case '*':
_mul();
break;
case '=':
_assign();
break;
}
}
// input is a complex number
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
else
{
stringstream ss(arg_input);
ss >> m_input_val;
_calc_result();
}
}
// main function
int main()
{
// create an instance of the class
BigReal_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
TA Version Code
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <iomanip>
using namespace std;
class BigReal_Calc;
class BigReal
{
private:
// data members
// save the digits before and after the decimal point of a before_decimal number
// with `long long` precision
const long long m_dec_upperbound = 1000000000;
long long m_before_decimal;
long long m_after_decimal; // times 10^-9
void _output_normalization();
public:
// Constructor, initializes before_decimal and after_decimalinary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
BigReal(const long long &arg_before_decimal = 0.0,
const long long &arg_after_decimal = 0.0);
// Copy constructor
BigReal(const BigReal &arg_big_real);
// assignment operator
BigReal &operator=(const BigReal &arg_big_real);
// add assignment operator
BigReal &operator+=(const BigReal &arg_big_real);
// multiply assignment operator
BigReal &operator*=(const BigReal &arg_big_real);
// add function
BigReal operator+(const BigReal &arg_big_real) const;
// multiply function
BigReal operator*(const BigReal &arg_big_real) const;
// cout `<<` operator for print BigReal number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal &arg_big_real);
// cin `>>` operator for input BigReal number
// note: be careful about the format of input
// hint: use string `+=` to append digits
friend istream &operator>>(istream &arg_is, BigReal &arg_big_real);
};
// BigReal calculator class declaration
class BigReal_Calc
{
private:
// define current value
BigReal m_curr_val;
// define input value
BigReal m_input_val;
// define operation
// `+`, `*`, and `=`
char m_op;
// calculate result
void _calc_result();
// operation functions
// add the input value to the current value
void _add();
// subtract the input value from the current value
void _mul();
// divide the current value by the input value
void _assign();
public:
// Constructor
BigReal_Calc();
// Copy constructor
BigReal_Calc(const BigReal_Calc &arg_int_calc);
// Destructor
~BigReal_Calc(){}; // no need to do anything
// set input value or operation
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal_Calc &arg_comp_calc);
};
// BigReal class implementation
void BigReal::_output_normalization()
{
if (m_after_decimal < 0)
{
m_before_decimal -= 1;
m_after_decimal += m_dec_upperbound;
}
if (m_after_decimal > m_dec_upperbound)
{
m_before_decimal += m_after_decimal / m_dec_upperbound;
m_after_decimal = m_after_decimal % m_dec_upperbound;
}
}
// Constructor, initializes before_decimal and after_decimalinary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
BigReal::BigReal(const long long &arg_before_decimal,
const long long &arg_after_decimal)
: m_before_decimal(arg_before_decimal), m_after_decimal(arg_after_decimal)
{
}
// Copy constructor
BigReal::BigReal(const BigReal &arg_big_real)
: m_before_decimal(arg_big_real.m_before_decimal),
m_after_decimal(arg_big_real.m_after_decimal)
{
}
// assignment operator
BigReal &BigReal::operator=(const BigReal &arg_big_real)
{
if (this == &arg_big_real) // self-assignment
return *this;
m_before_decimal = arg_big_real.m_before_decimal;
m_after_decimal = arg_big_real.m_after_decimal;
return *this;
}
// add assignment operator
BigReal &BigReal::operator+=(const BigReal &arg_big_real)
{
m_before_decimal += arg_big_real.m_before_decimal;
m_after_decimal += arg_big_real.m_after_decimal;
_output_normalization();
return *this;
}
// multiply assignment operator
BigReal &BigReal::operator*=(const BigReal &arg_big_real)
{
long long before_decimal = m_before_decimal * arg_big_real.m_before_decimal;
long long after_decimal = m_after_decimal * arg_big_real.m_after_decimal / m_dec_upperbound;
after_decimal += m_before_decimal * arg_big_real.m_after_decimal;
after_decimal += m_after_decimal * arg_big_real.m_before_decimal;
m_before_decimal = before_decimal;
m_after_decimal = after_decimal;
_output_normalization();
return *this;
}
// add function
BigReal BigReal::operator+(const BigReal &arg_big_real) const
{
BigReal c(*this);
c += arg_big_real;
return c;
}
// multiply function
BigReal BigReal::operator*(const BigReal &arg_big_real) const
{
BigReal c(*this);
c *= arg_big_real;
return c;
}
// cout `<<` operator for print BigReal number
// note: be careful about the format of output
ostream &operator<<(ostream &arg_os, const BigReal &arg_big_real)
{
arg_os << arg_big_real.m_before_decimal << '.'
<< setfill('0') << setw(9) << arg_big_real.m_after_decimal;
return arg_os;
}
// cin `>>` operator for input BigReal number
// note: be careful about the format of input
// hint: use string `+=` to append digits
istream &operator>>(istream &arg_is, BigReal &arg_big_real)
{
string str_before_decimal, str_after_decimal;
getline(arg_is, str_before_decimal, '.');
getline(arg_is, str_after_decimal);
str_after_decimal = str_after_decimal.substr(0, 9);
for (int i = 0; i < 9; i++)
if (i >= str_after_decimal.size())
str_after_decimal += '0';
stringstream ss_before_decimal(str_before_decimal);
ss_before_decimal >> arg_big_real.m_before_decimal;
stringstream ss_after_decimal(str_after_decimal);
ss_after_decimal >> arg_big_real.m_after_decimal;
return arg_is;
}
// BigReal_Calc class implementation
// Constructor
BigReal_Calc::BigReal_Calc()
: m_curr_val(), m_input_val(), m_op('=')
{
}
// Copy constructor
BigReal_Calc::BigReal_Calc(const BigReal_Calc &arg_int_calc)
: m_curr_val(arg_int_calc.m_curr_val),
m_input_val(arg_int_calc.m_input_val),
m_op(arg_int_calc.m_op)
{
}
// calculate the result
void BigReal_Calc::_calc_result()
{
switch (m_op)
{
case '+':
m_curr_val += m_input_val;
break;
case '*':
m_curr_val *= m_input_val;
break;
case '=':
m_curr_val = m_input_val;
break;
default:
break;
}
}
// add the input value to the current value
void BigReal_Calc::_add()
{
m_op = '+';
}
// multiply the input value with the current value
void BigReal_Calc::_mul()
{
m_op = '*';
}
// assign the input value to the current value
void BigReal_Calc::_assign()
{
m_op = '=';
}
// cout `<<` operator for print calculator status
ostream &operator<<(ostream &arg_os, const BigReal_Calc &arg_comp_calc)
{
arg_os << arg_comp_calc.m_curr_val;
return arg_os;
}
// parse the test cases, do not modify belows
void BigReal_Calc::set_input(const string &arg_input)
{
// input is empty, read again
if (arg_input.empty())
{
return;
}
// input is a operation
else if (arg_input == "+" || arg_input == "*" || arg_input == "=")
{
// set the activated operation
// as the same as the user press the op button
switch (arg_input[0])
{
case '+':
_add();
break;
case '*':
_mul();
break;
case '=':
_assign();
break;
}
}
// input is a complex number
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
else
{
stringstream ss(arg_input);
ss >> m_input_val;
_calc_result();
}
}
// main function
int main()
{
// create an instance of the class
BigReal_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
Midterm-3: Enhanced Big Positive Real Number Calculator (20%)
-
Inputs:
- Input a big positive real number in decimal point format, one line for one number.
- digits before and after the decimal point are at most 9 digits, separated by a point character
..
- digits before and after the decimal point are at most 9 digits, separated by a point character
- Input a operator, one line for one operator:
+: add*: multiply
- The input is interleaved, one line for one number and one line for one operator after the number.
- Input Ctrl+D to finish the input.
- Windows: Ctrl+Z (will show
^Zon the screen) then Enter (⏎in Format) to finish the input.
- Windows: Ctrl+Z (will show
- The input is any valid
stringtype.
- Input a big positive real number in decimal point format, one line for one number.
-
Outputs:
- The calculation result
- The result is shown in decimal point format, with at most 18 digits before the decimal point, and 9 digits after the decimal point (rounding toward zero, truncate).
- If the input is an operator, the program should print the current result in the following line. The format please refer to the Example section.
- If the input operand or operator is invalid, the program should print the error message
Error: Invalid inputand terminate the program.
- The calculation result
-
File name:
midterm-3_<student_id>.cpp(e.g.midterm-3_106062802.cpp) -
The program will not have any user prompts, only print the result.
-
The program only need to handle invalid inputs, i.e., invalid operand or operator. Other errors will be ingored.
-
Please based on
mainandBigReal_Calc::set_inputthat provided in the pseudo code to handle the input and output. -
The program should be finished within 10 seconds. Any test cases will garuntee the program is finished within 10 seconds.
Format
<before dec 1>.<after dec 1>⏎
<result 1>
<op 1>⏎
<result 1>
<before dec 2>.<after dec 2>⏎
<result 2>
<op 2>⏎
<result 2>
...
<before dec n-1>.<after dec n-1>⏎
<result n-1>
<op n-1>⏎
<result n-1>
<before dec n>.<after dec n>⏎
<result n>
^Z⏎
Example
Normal
$ ./a.out
1.0⏎
1.000000000
^Z⏎
$ ./a.out
0.2⏎
0.200000000
^Z⏎
$ ./a.out
000000000.000000000⏎
0.000000000
^Z⏎
$ ./a.out
1.0⏎
1.000000000
+⏎
1.000000000
2.0⏎
3.000000000
+⏎
3.000000000
3.0⏎
6.000000000
*⏎
6.000000000
4.3⏎
25.800000000
^Z⏎
$ ./a.out
1.000000001⏎
1.000000001
+⏎
1.000000001
2.000000002⏎
3.000000003
^Z⏎
$ ./a.out
123456789.123456789⏎
123456789.123456789
+⏎
123456789.123456789
987654321.987654321⏎
1111111111.111111110
^Z⏎
$ ./a.out
1.000000001⏎
1.000000001
*⏎
1.000000001
2.000000002⏎
2.000000004
^Z⏎
$ ./a.out
123456789.123456789⏎
123456789.123456789
*⏎
123456789.123456789
987654321.987654321⏎
121932631356500531.347203169
^Z⏎
Exception Handling
$ ./a.out
+⏎
Error: Invalid input
$
$ ./a.out
1.0⏎
1.000000000
1.0⏎
Error: Invalid input
$
$ ./a.out
1.0⏎
1.000000000
+⏎
1.000000000
+⏎
Error: Invalid input
$
$ ./a.out
1.0 2.0⏎
Error: Invalid input
$
$ ./a.out
1234567890.0⏎
Error: Invalid input
$
$ ./a.out
0000000000.0⏎
Error: Invalid input
$
$ ./a.out
123456789.1234567890⏎
Error: Invalid input
$
$ ./a.out
123456789.0⏎
Error: Invalid input
$
$ ./a.out
1.0⏎
1.000000000
sdafsdagret⏎
Error: Invalid input
$
$ ./a.out
sdoifjwepoirjpwoie⏎
Error: Invalid input
$
$ ./a.out
1.⏎
Error: Invalid input
$
$ ./a.out
.90⏎
Error: Invalid input
$
Reference
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <iomanip>
#include <cctype>
using namespace std;
class BigReal_Calc;
class BigReal
{
private:
// data members
// save the digits before and after the decimal point of a before_decimal number
// with `long long` precision
const long long m_dec_upperbound = 1000000000;
long long m_before_decimal;
long long m_after_decimal; // times 10^-9
void _output_normalization();
public:
// Constructor, initializes before_decimal and after_decimalinary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
BigReal(const long long &arg_before_decimal = 0.0,
const long long &arg_after_decimal = 0.0);
// Copy constructor
BigReal(const BigReal &arg_big_real);
// assignment operator
BigReal &operator=(const BigReal &arg_big_real);
// add assignment operator
BigReal &operator+=(const BigReal &arg_big_real);
// multiply assignment operator
BigReal &operator*=(const BigReal &arg_big_real);
// add function
BigReal operator+(const BigReal &arg_big_real) const;
// multiply function
BigReal operator*(const BigReal &arg_big_real) const;
// cout `<<` operator for print BigReal number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal &arg_big_real);
// cin `>>` operator for input BigReal number
// note: be careful about the format of input
// hint: use string `+=` to append digits
friend istream &operator>>(istream &arg_is, BigReal &arg_big_real);
};
// BigReal calculator class declaration
class BigReal_Calc
{
private:
// define current value
BigReal m_curr_val;
// define input value
BigReal m_input_val;
// define operation
// `+`, `*`, and `=`
char m_op;
// define input status, truns `op` for true and turns `value` for false
bool m_op_input;
// calculate result
void _calc_result();
// operation functions
// set activation op to add
void _add();
// set activation op to subtract
void _mul();
// set activation op to divide
void _assign();
public:
// Constructor
BigReal_Calc();
// Copy constructor
BigReal_Calc(const BigReal_Calc &arg_int_calc);
// Destructor
~BigReal_Calc(){}; // no need to do anything
// set input value or operation
// as the same as the user input number or operation
// into the calculator
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal_Calc &arg_comp_calc);
};
// error and exit
void error_and_exit()
{
cerr << "Error: Invalid input" << endl;
exit(1);
}
void BigReal_Calc::set_input(const string &arg_input)
{
if (arg_input.empty())
{
return;
}
// input is a operation
else if ()
{
// set the activated operation
// as the same as the user press the op button
switch (arg_input[0])
{
case '+':
_add();
break;
case '*':
_mul();
break;
case '=':
_assign();
break;
}
// set to 'input a complex number' turn
}
// input is a complex number
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
else if ()
{
stringstream ss(arg_input);
ss >> m_input_val;
_calc_result();
// set to 'input a op' turn
}
else
{
error_and_exit();
}
}
// main function
int main()
{
// create an instance of the class
BigReal_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
TA Version Code
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <iomanip>
#include <cctype>
using namespace std;
class BigReal_Calc;
class BigReal
{
private:
// data members
// save the digits before and after the decimal point of a before_decimal number
// with `long long` precision
const long long m_dec_upperbound = 1000000000;
long long m_before_decimal;
long long m_after_decimal; // times 10^-9
void _output_normalization();
public:
// Constructor, initializes before_decimal and after_decimalinary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
BigReal(const long long &arg_before_decimal = 0.0,
const long long &arg_after_decimal = 0.0);
// Copy constructor
BigReal(const BigReal &arg_big_real);
// assignment operator
BigReal &operator=(const BigReal &arg_big_real);
// add assignment operator
BigReal &operator+=(const BigReal &arg_big_real);
// multiply assignment operator
BigReal &operator*=(const BigReal &arg_big_real);
// add function
BigReal operator+(const BigReal &arg_big_real) const;
// multiply function
BigReal operator*(const BigReal &arg_big_real) const;
// cout `<<` operator for print BigReal number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal &arg_big_real);
// cin `>>` operator for input BigReal number
// note: be careful about the format of input
// hint: use string `+=` to append digits
friend istream &operator>>(istream &arg_is, BigReal &arg_big_real);
};
// BigReal calculator class declaration
class BigReal_Calc
{
private:
// define current value
BigReal m_curr_val;
// define input value
BigReal m_input_val;
// define operation
// `+`, `*`, and `=`
char m_op;
// define input status, truns `op` for true and turns `value` for false
bool m_op_input;
// calculate result
void _calc_result();
// operation functions
// set activation op to add
void _add();
// set activation op to subtract
void _mul();
// set activation op to divide
void _assign();
public:
// Constructor
BigReal_Calc();
// Copy constructor
BigReal_Calc(const BigReal_Calc &arg_int_calc);
// Destructor
~BigReal_Calc(){}; // no need to do anything
// set input value or operation
// as the same as the user input number or operation
// into the calculator
void set_input(const string &arg_input);
// cout `<<` operator for print calculator status
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const BigReal_Calc &arg_comp_calc);
};
// error and exit
void error_and_exit()
{
cerr << "Error: Invalid input" << endl;
exit(1);
}
// BigReal class implementation
void BigReal::_output_normalization()
{
if (m_after_decimal < 0)
{
m_before_decimal -= 1;
m_after_decimal += m_dec_upperbound;
}
if (m_after_decimal > m_dec_upperbound)
{
m_before_decimal += m_after_decimal / m_dec_upperbound;
m_after_decimal = m_after_decimal % m_dec_upperbound;
}
}
// Constructor, initializes before_decimal and after_decimalinary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
BigReal::BigReal(const long long &arg_before_decimal,
const long long &arg_after_decimal)
: m_before_decimal(arg_before_decimal), m_after_decimal(arg_after_decimal)
{
}
// Copy constructor
BigReal::BigReal(const BigReal &arg_big_real)
: m_before_decimal(arg_big_real.m_before_decimal),
m_after_decimal(arg_big_real.m_after_decimal)
{
}
// assignment operator
BigReal &BigReal::operator=(const BigReal &arg_big_real)
{
if (this == &arg_big_real) // self-assignment
return *this;
m_before_decimal = arg_big_real.m_before_decimal;
m_after_decimal = arg_big_real.m_after_decimal;
return *this;
}
// add assignment operator
BigReal &BigReal::operator+=(const BigReal &arg_big_real)
{
m_before_decimal += arg_big_real.m_before_decimal;
m_after_decimal += arg_big_real.m_after_decimal;
_output_normalization();
return *this;
}
// multiply assignment operator
BigReal &BigReal::operator*=(const BigReal &arg_big_real)
{
long long before_decimal = m_before_decimal * arg_big_real.m_before_decimal;
long long after_decimal = m_after_decimal * arg_big_real.m_after_decimal / m_dec_upperbound;
after_decimal += m_before_decimal * arg_big_real.m_after_decimal;
after_decimal += m_after_decimal * arg_big_real.m_before_decimal;
m_before_decimal = before_decimal;
m_after_decimal = after_decimal;
_output_normalization();
return *this;
}
// add function
BigReal BigReal::operator+(const BigReal &arg_big_real) const
{
BigReal c(*this);
c += arg_big_real;
return c;
}
// multiply function
BigReal BigReal::operator*(const BigReal &arg_big_real) const
{
BigReal c(*this);
c *= arg_big_real;
return c;
}
// cout `<<` operator for print BigReal number
// note: be careful about the format of output
ostream &operator<<(ostream &arg_os, const BigReal &arg_big_real)
{
arg_os << arg_big_real.m_before_decimal << '.'
<< setfill('0') << setw(9) << arg_big_real.m_after_decimal;
return arg_os;
}
// cin `>>` operator for input BigReal number
// note: be careful about the format of input
// hint: use string `+=` to append digits
istream &operator>>(istream &arg_is, BigReal &arg_big_real)
{
string str_before_decimal, str_after_decimal;
getline(arg_is, str_before_decimal, '.');
if (str_before_decimal.empty() || str_before_decimal.size() > 9)
{
error_and_exit();
}
getline(arg_is, str_after_decimal);
if (str_after_decimal.empty() || str_after_decimal.size() > 9 || !arg_is.eof())
{
error_and_exit();
}
for (int i = 0; i < 9; i++)
{
if (i >= str_after_decimal.size())
{
str_after_decimal += '0';
}
else if (!isdigit(str_after_decimal[i]))
{
error_and_exit();
}
}
stringstream ss_before_decimal(str_before_decimal);
ss_before_decimal >> arg_big_real.m_before_decimal;
if (ss_before_decimal.fail())
{
error_and_exit();
}
stringstream ss_after_decimal(str_after_decimal);
ss_after_decimal >> arg_big_real.m_after_decimal;
if (ss_after_decimal.fail())
{
error_and_exit();
}
return arg_is;
}
// BigReal_Calc class implementation
// Constructor
BigReal_Calc::BigReal_Calc()
: m_curr_val(), m_input_val(), m_op('='), m_op_input(false)
{
}
// Copy constructor
BigReal_Calc::BigReal_Calc(const BigReal_Calc &arg_int_calc)
: m_curr_val(arg_int_calc.m_curr_val),
m_input_val(arg_int_calc.m_input_val),
m_op(arg_int_calc.m_op),
m_op_input(arg_int_calc.m_op_input)
{
}
// calculate the result
void BigReal_Calc::_calc_result()
{
switch (m_op)
{
case '+':
m_curr_val += m_input_val;
break;
case '*':
m_curr_val *= m_input_val;
break;
case '=':
m_curr_val = m_input_val;
break;
default:
error_and_exit();
}
}
// set activation op to add
void BigReal_Calc::_add()
{
m_op = '+';
}
// set activation op to multiply
void BigReal_Calc::_mul()
{
m_op = '*';
}
// set activation op to assign
void BigReal_Calc::_assign()
{
m_op = '=';
}
// cout `<<` operator for print calculator status
ostream &operator<<(ostream &arg_os, const BigReal_Calc &arg_comp_calc)
{
arg_os << arg_comp_calc.m_curr_val;
return arg_os;
}
void BigReal_Calc::set_input(const string &arg_input)
{
if (arg_input.empty())
{
return;
}
// input is a operation
else if (m_op_input && (arg_input == "+" || arg_input == "*" || arg_input == "="))
{
// set the activated operation
// as the same as the user press the op button
switch (arg_input[0])
{
case '+':
_add();
break;
case '*':
_mul();
break;
case '=':
_assign();
break;
}
// set to 'input a complex number' turn
m_op_input = false;
}
// input is a complex number
// as the same as the user type a number
// it performs as the same as the user pressed the '=' button
// if the input is the first input
// thus, we initialize the m_op to '='
else if (!m_op_input)
{
stringstream ss(arg_input);
ss >> m_input_val;
_calc_result();
// set to 'input a op' turn
m_op_input = true;
}
else
{
error_and_exit();
}
}
// main function
int main()
{
// create an instance of the class
BigReal_Calc calc;
string input;
while (getline(cin, input))
{
calc.set_input(input);
cout << calc << endl;
}
}
OOP: Inheritance (2)
Slides version: lecture10_slides.html Website version: lecture10.html
- Recap Inheritance
- Example: Bus, Car, and Truck
- Inheritance Mode
- Friend function & Inheritance (public, protected, private)
- Inheritance Type
- Single, Multiple, Multi-level (discuss in the previous lecture)
- Hierarchical
- Hybrid
- Multipath inheritance
- Inheritance in Software Engineering
- Reusable & Efficient
- Is a (Inheritance) & Has a (Composition)
- Example 1: Integer & Real & Complex Number Calculator
- Example 2: Complex Number & Triangle
- Example 3: Complex Number & Triangles
Recap Inheritance
Ref: Inheritance in C++
Example: Bus, Car, and Truck.

Because bus, car and truck are all vehicles, and they all have the same member functions, we can use inheritance to reduce the amount of code we need to write. For example, class Vehicle:

Example: Bus, Car, and Truck.
#include <iostream>
using namespace std;
class Vehicle
{
public:
void run()
{
std::cout << "Vehicle is running" << std::endl;
}
};
class Bus : public Vehicle
{
};
class Car : public Vehicle
{
};
class Truck : public Vehicle
{
};
int main()
{
Bus bus;
Car car;
Truck truck;
bus.run();
car.run();
truck.run();
return 0;
}
Output:
$ ./a.out
Vehicle is running
Vehicle is running
Vehicle is running
Inheritance Mode
| Class Member Type | Type of | Inheritence | |
|---|---|---|---|
| Public | Protected | Private | |
| Public | Public | Protected | Private |
| Protected | Protected | Protected | Private |
| Private | Not accessible | Not accessible | Not accessible |
Friend function & Inheritance
class A
{
public:
int x;
friend void f_x(A &a)
{
a.x = 1;
}
protected:
int y;
friend void f_y(A &a)
{
a.y = 2;
}
private:
int z;
friend void f_z(A &a)
{
a.z = 3;
}
};
class B : public A
{
// x is public
// y is protected
// z is not accessible from B
};
class C : protected A
{
// x is protected
// y is protected
// z is not accessible from C
};
class D : private A // 'private' is default for classes
{
// x is private
// y is private
// z is not accessible from D
};
int main()
{
A a;
B b;
C c;
D d;
f_x(a);
f_y(a);
f_z(a);
f_x(b);
f_y(b);
f_z(b);
f_x(c); // error: not accessible
f_y(c); // error: not accessible
f_z(c); // error: not accessible
f_x(d); // error: not accessible
f_y(d); // error: not accessible
f_z(d); // error: not accessible
return 0;
}
Inheritance Type
- Single (discuss in the previous lecture)
- Multiple (discuss in the previous lecture)
- Multi-level (discuss in the previous lecture)
- Hierarchical
- Hybrid (Virtual) Inheritance
- Multipath inheritance
Hierarchical Inheritance
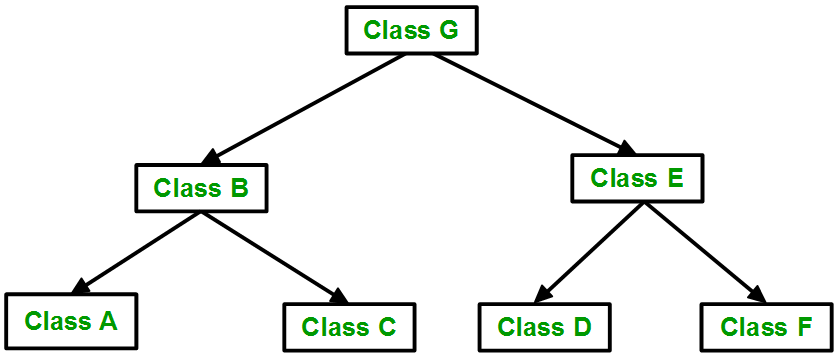
// C++ program to implement
// Hierarchical Inheritance
#include <iostream>
using namespace std;
// base class
class Vehicle
{
public:
Vehicle()
{
cout << "This is a Vehicle\n";
}
};
// first sub class
class Car : public Vehicle
{
};
// second sub class
class Bus : public Vehicle
{
};
// main function
int main()
{
// Creating object of sub class will
// invoke the constructor of base class.
Car obj1;
Bus obj2;
return 0;
}
Hybrid (Virtual) Inheritance
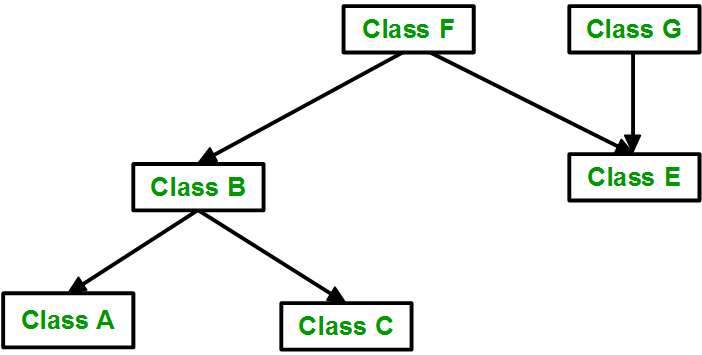
// C++ program to explain
// multiple inheritance
#include <iostream>
using namespace std;
// first base class
class Vehicle
{
public:
Vehicle()
{
cout << "This is a Vehicle\n";
}
};
// second base class
class FourWheeler
{
public:
FourWheeler()
{
cout << "This is a 4 wheeler Vehicle\n";
}
};
// sub class derived from two base classes
class Car : public Vehicle, public FourWheeler
{
};
// main function
int main()
{
// Creating object of sub class will
// invoke the constructor of base classes.
Car obj;
return 0;
}
Multipath inheritance
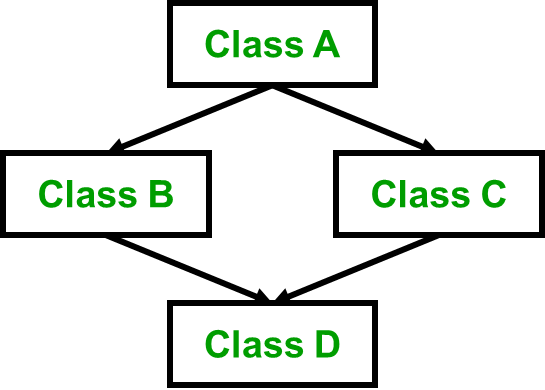
#include <iostream>
class ClassA
{
public:
int a;
};
class ClassB : virtual public ClassA
{
public:
int b;
};
class ClassC : virtual public ClassA
{
public:
int c;
};
class ClassD : public ClassB, public ClassC
{
public:
int d;
};
int main()
{
ClassD obj;
obj.a = 10; // Statement 3
obj.a = 100; // Statement 4
obj.b = 20;
obj.c = 30;
obj.d = 40;
cout << "\n a : " << obj.a;
cout << "\n b : " << obj.b;
cout << "\n c : " << obj.c;
cout << "\n d : " << obj.d << '\n';
}
Inheritance in Software Engineering
Why use inheritance?
Inheritance is used all the time when writing object-oriented code. In most OO languages, (with C++ being a prominent exception,) all objects have a single "base object" class that they derive from that provides common functionality, so literally everything that uses an object uses inheritance.
Ref: Mason Wheeler
Why use inheritance?
- Reuse code
- You can reuse code by inheriting from a class without having to copy/paste the code.
- Also, you can reuse pre-built codes with inheritance.
- Code integrity
- You can ensure that your code is consistent, i.e. the structure of the code is the same for all derived classes.
Pros of Inheritance
Advantages:
- Inheritance promotes reusability. When a class inherits or derives another class, it can access all the functionality of inherited class.
- Reusability enhanced reliability. The base class code will be already tested and debugged.
- As the existing code is reused, it leads to less development and maintenance costs.
- Inheritance makes the sub classes follow a standard interface.
- Inheritance helps to reduce code redundancy and supports code extensibility.
- Inheritance facilitates creation of class libraries.
Ref: vaishali bhatia
Cons of Inheritance
Disadvantages:
- Inherited functions work slower than normal function as there is indirection.
- Improper use of inheritance may lead to wrong solutions.
- Often, data members in the base class are left unused which may lead to memory wastage.
- Inheritance increases the coupling between base class and derived class. A change in base class will affect all the child classes.
Ref: vaishali bhatia
Is a (Inheritance) & Has a (Composition)
When to use inheritance?
- If object B is an object A, then inheritance is used.
- e.g. an apple is a fruit, so inheritance is used.
When to use composition?
- If object B has object A, then composition is used.
- e.g. a car has a engine, so composition is used.
Pitfall: Use Inheritance in Has-a Relationship
class Legs
{
public:
void WalkAround() {... code for walking around goes here... }
};
class Arms
{
public:
void GrabThings() {... code for grabbing things goes here... }
};
class InheritanceRobot : public Legs, public Arms
{
public:
// WalkAround() and GrabThings() methods are implicitly
// defined for this class since it inherited those
// methods from its two superclasses
};
class CompositionRobot
{
public:
void WalkAround() { legs.WalkAround(); }
void GrabThings() { arms.GrabThings(); }
private:
Legs legs;
Arms arms;
};
Ref: Jeremy Friesner
Example 1: Integer & Real & Complex Number Calculator [Source]
Example 2: Complex Number & Triangle [Source]
Example 3: Complex Number & Triangles [Source]
Example 1: Integer & Real & Complex Number Calculator
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Integer
{
protected:
int m_int_value;
public:
Integer(int arg_int_value = 0) : m_int_value(arg_int_value)
{
}
Integer(const Integer &arg_int) : m_int_value(arg_int.m_int_value)
{
}
operator int() const
{
return m_int_value;
}
Integer &operator=(const Integer &arg_int)
{
m_int_value = arg_int.m_int_value;
return *this;
}
void set_int_value(int arg_int_value)
{
m_int_value = arg_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Integer &arg_integer)
{
arg_os << arg_integer.m_int_value;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Integer &arg_integer)
{
arg_is >> arg_integer.m_int_value;
return arg_is;
}
friend Integer operator+(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value + arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator-(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value - arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator*(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value * arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator/(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value / arg_integer2.m_int_value);
return temp_integer;
}
};
// Real is a Integer
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value = 0.0) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
Real(const Real &arg_real) : Integer(arg_real),
m_after_decimal(arg_real.m_after_decimal)
{
}
operator double() const
{
return m_after_decimal + (double)m_int_value;
}
Real &operator=(const Real &arg_real)
{
m_int_value = arg_real.m_int_value;
m_after_decimal = arg_real.m_after_decimal;
return *this;
}
void set_real_value(double arg_value)
{
m_int_value = (int)arg_value;
m_after_decimal = arg_value - m_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Real &arg_real)
{
arg_os << (double)arg_real;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Real &arg_real)
{
double temp_double;
arg_is >> temp_double;
arg_real.set_real_value(temp_double);
return arg_is;
}
friend Real operator+(const Real &arg_real1, const Real &arg_real2)
{
// call the Integer operator+ to add the Integer part
Integer temp_integer((Integer)arg_real1 + (Integer)arg_real2);
Real temp_real(arg_real1.m_after_decimal + arg_real2.m_after_decimal);
temp_real.set_int_value((int)temp_integer + (int)temp_real);
return temp_real;
}
friend Real operator-(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 - (double)arg_real2);
return temp_real;
}
friend Real operator*(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 * (double)arg_real2);
return temp_real;
}
friend Real operator/(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 / (double)arg_real2);
return temp_real;
}
};
class Imaginary
{
protected:
double m_imaginary_value;
public:
Imaginary(double arg_imaginary_value = 0.0) : m_imaginary_value(arg_imaginary_value)
{
}
Imaginary(const Imaginary &arg_imaginary) : m_imaginary_value(arg_imaginary.m_imaginary_value)
{
}
Imaginary &operator=(const Imaginary &arg_imaginary)
{
m_imaginary_value = arg_imaginary.m_imaginary_value;
return *this;
}
double get_imaginary_value() const
{
return m_imaginary_value;
}
void set_imaginary_value(double arg_imaginary_value)
{
m_imaginary_value = arg_imaginary_value;
}
friend ostream &operator<<(ostream &arg_os, const Imaginary &arg_imaginary)
{
arg_os << arg_imaginary.m_imaginary_value << "i";
return arg_os;
}
friend Imaginary operator+(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value + arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
friend Imaginary operator-(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value - arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
};
class Complex : public Real, public Imaginary
{
public:
Complex(double arg_real_value = 0.0,
double arg_imaginary_value = 0.0)
: Real(arg_real_value),
Imaginary(arg_imaginary_value)
{
}
Complex(const Complex &arg_complex)
: Real(arg_complex),
Imaginary(arg_complex)
{
}
Complex &operator=(const Complex &arg_complex)
{
Real::operator=(arg_complex);
Imaginary::operator=(arg_complex);
return *this;
}
Complex reciprocal() const
{
Complex temp_complex(*this);
double temp_real_value = temp_complex;
double temp_imaginary_value = temp_complex.get_imaginary_value();
double temp_denominator = temp_real_value * temp_real_value + temp_imaginary_value * temp_imaginary_value;
temp_complex.set_real_value(temp_real_value / temp_denominator);
temp_complex.set_imaginary_value(-temp_imaginary_value / temp_denominator);
return temp_complex;
}
friend ostream &operator<<(ostream &arg_os, const Complex &arg_complex)
{
arg_os << (Real)arg_complex << " + " << (Imaginary)arg_complex;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Complex &arg_complex)
{
string temp_string;
getline(arg_is, temp_string);
size_t plus_pos = temp_string.find("+");
if (plus_pos != string::npos)
{
arg_complex.set_real_value(atof(temp_string.substr(0, plus_pos).c_str()));
}
size_t i_pos = temp_string.find("i");
if (i_pos != string::npos)
{
arg_complex.set_imaginary_value(
atof(temp_string.substr(plus_pos + 1, i_pos - plus_pos - 1)
.c_str()));
}
return arg_is;
}
friend Complex operator+(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 + (double)arg_complex2,
arg_complex1.get_imaginary_value() + arg_complex2.get_imaginary_value());
return temp_complex;
}
friend Complex operator-(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 - (double)arg_complex2,
arg_complex1.get_imaginary_value() - arg_complex2.get_imaginary_value());
return temp_complex;
}
friend Complex operator*(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 * (double)arg_complex2 -
arg_complex1.get_imaginary_value() * arg_complex2.get_imaginary_value(),
(double)arg_complex1 * arg_complex2.get_imaginary_value() +
arg_complex1.get_imaginary_value() * (double)arg_complex2);
return temp_complex;
}
friend Complex operator/(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex(arg_complex1 * arg_complex2.reciprocal());
return temp_complex;
}
};
// Complex calculator class declaration
class Complex_Calc
{
private:
// define current value
Complex m_curr_val;
// define input value
Complex m_input_val;
// define operation
// `+`, `-`, `*`, `/`, and `=`
char m_op;
// define input status, turns `op` for true and turns `value` for false
bool m_op_input;
// calculate result
void _calc_result()
{
switch (m_op)
{
case '+':
m_curr_val = m_curr_val + m_input_val;
break;
case '-':
m_curr_val = m_curr_val - m_input_val;
break;
case '*':
m_curr_val = m_curr_val * m_input_val;
break;
case '/':
m_curr_val = m_curr_val / m_input_val;
break;
case '=':
m_curr_val = m_input_val;
break;
default:
break;
}
}
// operation functions
// set activation op to add
void _add()
{
m_op = '+';
m_op_input = false;
}
// set activation op to subtract
void _sub()
{
m_op = '-';
m_op_input = false;
}
// set activation op to multiply
void _mul()
{
m_op = '*';
m_op_input = false;
}
// set activation op to divide
void _div()
{
m_op = '/';
m_op_input = false;
}
// set activation op to assign
void _assign()
{
m_op = '=';
m_op_input = false;
}
public:
// Constructor
Complex_Calc()
: m_curr_val(), m_input_val(), m_op('='), m_op_input(false)
{
}
// Copy constructor
Complex_Calc(const Complex_Calc &arg_comp_calc)
: m_curr_val(arg_comp_calc.m_curr_val), m_input_val(arg_comp_calc.m_input_val),
m_op(arg_comp_calc.m_op), m_op_input(arg_comp_calc.m_op_input)
{
}
// Destructor
~Complex_Calc(){}; // no need to do anything
// cin `>>` operator for set input value or operation
friend istream &operator>>(istream &arg_is, Complex_Calc &arg_comp_calc)
{
string temp_string;
getline(arg_is, temp_string);
if (temp_string == "+")
{
arg_comp_calc._add();
}
else if (temp_string == "-")
{
arg_comp_calc._sub();
}
else if (temp_string == "*")
{
arg_comp_calc._mul();
}
else if (temp_string == "/")
{
arg_comp_calc._div();
}
else if (temp_string == "=")
{
arg_comp_calc._assign();
}
else
{
stringstream temp_string_stream(temp_string);
temp_string_stream >> arg_comp_calc.m_input_val;
arg_comp_calc.m_op_input = true;
arg_comp_calc._calc_result();
}
return arg_is;
}
// cout `<<` operator for print calculator status
// note: be careful about the format of output
// cout `<<` operator for print calculator status
friend ostream &operator<<(ostream &arg_os, const Complex_Calc &arg_comp_calc)
{
arg_os << arg_comp_calc.m_curr_val;
return arg_os;
}
};
int main()
{
// create an instance of the class
Complex_Calc calc;
while (cin >> calc)
{
cout << calc << endl;
}
}
Example 2: Complex Number & Triangle
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Triangle_Complex; // forward declaration
class Integer
{
protected:
int m_int_value;
public:
Integer(int arg_int_value = 0) : m_int_value(arg_int_value)
{
}
Integer(const Integer &arg_int) : m_int_value(arg_int.m_int_value)
{
}
operator int() const
{
return m_int_value;
}
Integer &operator=(const Integer &arg_int)
{
m_int_value = arg_int.m_int_value;
return *this;
}
void set_int_value(int arg_int_value)
{
m_int_value = arg_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Integer &arg_integer)
{
arg_os << arg_integer.m_int_value;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Integer &arg_integer)
{
arg_is >> arg_integer.m_int_value;
return arg_is;
}
friend Integer operator+(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value + arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator-(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value - arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator*(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value * arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator/(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value / arg_integer2.m_int_value);
return temp_integer;
}
};
// Real is a Integer
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value = 0.0) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
Real(const Real &arg_real) : Integer(arg_real),
m_after_decimal(arg_real.m_after_decimal)
{
}
operator double() const
{
return m_after_decimal + (double)m_int_value;
}
Real &operator=(const Real &arg_real)
{
m_int_value = arg_real.m_int_value;
m_after_decimal = arg_real.m_after_decimal;
return *this;
}
void set_real_value(double arg_value)
{
m_int_value = (int)arg_value;
m_after_decimal = arg_value - m_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Real &arg_real)
{
arg_os << (double)arg_real;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Real &arg_real)
{
double temp_double;
arg_is >> temp_double;
arg_real.set_real_value(temp_double);
return arg_is;
}
friend Real operator+(const Real &arg_real1, const Real &arg_real2)
{
// call the Integer operator+ to add the Integer part
Integer temp_integer((Integer)arg_real1 + (Integer)arg_real2);
Real temp_real(arg_real1.m_after_decimal + arg_real2.m_after_decimal);
temp_real.set_int_value((int)temp_integer + (int)temp_real);
return temp_real;
}
friend Real operator-(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 - (double)arg_real2);
return temp_real;
}
friend Real operator*(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 * (double)arg_real2);
return temp_real;
}
friend Real operator/(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 / (double)arg_real2);
return temp_real;
}
};
class Imaginary
{
protected:
double m_imaginary_value;
public:
Imaginary(double arg_imaginary_value = 0.0) : m_imaginary_value(arg_imaginary_value)
{
}
Imaginary(const Imaginary &arg_imaginary) : m_imaginary_value(arg_imaginary.m_imaginary_value)
{
}
Imaginary &operator=(const Imaginary &arg_imaginary)
{
m_imaginary_value = arg_imaginary.m_imaginary_value;
return *this;
}
double get_imaginary_value() const
{
return m_imaginary_value;
}
void set_imaginary_value(double arg_imaginary_value)
{
m_imaginary_value = arg_imaginary_value;
}
friend ostream &operator<<(ostream &arg_os, const Imaginary &arg_imaginary)
{
arg_os << arg_imaginary.m_imaginary_value << "i";
return arg_os;
}
friend Imaginary operator+(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value + arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
friend Imaginary operator-(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value - arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
};
class Complex : public Real, public Imaginary
{
public:
Complex(double arg_real_value = 0.0,
double arg_imaginary_value = 0.0)
: Real(arg_real_value),
Imaginary(arg_imaginary_value)
{
}
Complex(const Complex &arg_complex)
: Real(arg_complex),
Imaginary(arg_complex)
{
}
Complex &operator=(const Complex &arg_complex)
{
Real::operator=(arg_complex);
Imaginary::operator=(arg_complex);
return *this;
}
Complex reciprocal() const
{
Complex temp_complex(*this);
double temp_real_value = temp_complex;
double temp_imaginary_value = temp_complex.get_imaginary_value();
double temp_denominator = temp_real_value * temp_real_value + temp_imaginary_value * temp_imaginary_value;
temp_complex.set_real_value(temp_real_value / temp_denominator);
temp_complex.set_imaginary_value(-temp_imaginary_value / temp_denominator);
return temp_complex;
}
friend ostream &operator<<(ostream &arg_os, const Complex &arg_complex)
{
arg_os << (Real)arg_complex << " + " << (Imaginary)arg_complex;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Complex &arg_complex)
{
string temp_string;
getline(arg_is, temp_string, '+');
arg_complex.set_real_value(stod(temp_string));
getline(arg_is, temp_string, 'i');
arg_complex.set_imaginary_value(stod(temp_string));
return arg_is;
}
friend Complex operator+(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 + (double)arg_complex2,
arg_complex1.get_imaginary_value() + arg_complex2.get_imaginary_value());
return temp_complex;
}
friend Complex operator-(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 - (double)arg_complex2,
arg_complex1.get_imaginary_value() - arg_complex2.get_imaginary_value());
return temp_complex;
}
friend Complex operator*(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 * (double)arg_complex2 -
arg_complex1.get_imaginary_value() * arg_complex2.get_imaginary_value(),
(double)arg_complex1 * arg_complex2.get_imaginary_value() +
arg_complex1.get_imaginary_value() * (double)arg_complex2);
return temp_complex;
}
friend Complex operator/(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex(arg_complex1 * arg_complex2.reciprocal());
return temp_complex;
}
friend bool operator==(const Complex &arg_complex1, const Complex &arg_complex2)
{
return ((double)arg_complex1 == (double)arg_complex2) &&
(arg_complex1.get_imaginary_value() == arg_complex2.get_imaginary_value());
}
friend bool operator!=(const Complex &arg_complex1, const Complex &arg_complex2)
{
return !(arg_complex1 == arg_complex2);
}
friend bool operator<(const Complex &arg_complex1, const Complex &arg_complex2)
{
return ((double)arg_complex1 < (double)arg_complex2) ||
((double)arg_complex1 == (double)arg_complex2 &&
arg_complex1.get_imaginary_value() < arg_complex2.get_imaginary_value());
}
friend bool operator>(const Complex &arg_complex1, const Complex &arg_complex2)
{
return arg_complex2 < arg_complex1;
}
friend bool operator<=(const Complex &arg_complex1, const Complex &arg_complex2)
{
return !(arg_complex1 > arg_complex2);
}
friend bool operator>=(const Complex &arg_complex1, const Complex &arg_complex2)
{
return !(arg_complex1 < arg_complex2);
}
friend class Triangle_Complex;
};
// Triangle_Complex class declaration
class Triangle_Complex
{
private:
// define three points of the Triangle_Complex
// Triangle 'has-a' Complex, so it use composition
Complex m_point[3];
// check & correct the Triangle_Complex points to counterclockwise order
void _check_points()
{
// if the area is negative, swap the points
if (area() < 0.0)
{
Complex temp = m_point[0];
m_point[0] = m_point[1];
m_point[1] = temp;
}
}
public:
// Constructor
Triangle_Complex(const Complex &arg_point1,
const Complex &arg_point2,
const Complex &arg_point3)
: m_point{arg_point1, arg_point2, arg_point3}
{
_check_points();
}
// Copy constructor
Triangle_Complex(const Triangle_Complex &arg_triangle)
: m_point{arg_triangle.m_point[0], arg_triangle.m_point[1], arg_triangle.m_point[2]}
{
}
// Destructor
~Triangle_Complex() {} // do nothing
// modify the three points of the Triangle_Complex
void set_points(const Complex &arg_point1,
const Complex &arg_point2,
const Complex &arg_point3)
{
m_point[0] = arg_point1;
m_point[1] = arg_point2;
m_point[2] = arg_point3;
_check_points();
}
void set_point1(const Complex &arg_point1)
{
m_point[0] = arg_point1;
_check_points();
}
void set_point2(const Complex &arg_point2)
{
m_point[1] = arg_point2;
_check_points();
}
void set_point3(const Complex &arg_point3)
{
m_point[2] = arg_point3;
_check_points();
}
// get the three points of the Triangle_Complex
Complex get_point1() const
{
return m_point[0];
}
Complex get_point2() const
{
return m_point[1];
}
Complex get_point3() const
{
return m_point[2];
}
// calculate the area of the Triangle_Complex
double area()
{
double area = 0.0;
for (int i = 0; i < 3; i++)
{
area += (double)m_point[i] * m_point[(i + 1) % 3].get_imaginary_value();
area -= m_point[i].get_imaginary_value() * (double)m_point[(i + 1) % 3];
}
return area / 2.0;
}
// print the Triangle_Complex
// format: (c1, c2, c3)
friend std::ostream &operator<<(std::ostream &arg_os, const Triangle_Complex &arg_tri)
{
arg_os << "(";
for (int i = 0; i < 3; i++)
{
arg_os << arg_tri.m_point[i];
if (i < 2)
arg_os << ", ";
}
arg_os << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: (c1, c2, c3) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Triangle_Complex &arg_tri)
{
string temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
for (int i = 0; i < 3; i++)
{
arg_is >> arg_tri.m_point[i];
if (i < 2)
{
getline(arg_is, temp, ','); // ignore the ','
}
}
getline(arg_is, temp, ')'); // ignore the last ')'
}
// check & correct the Triangle_Complex points to counterclockwise order
arg_tri._check_points();
return arg_is;
}
};
// main function
int main()
{
Triangle_Complex t(Complex(1, 1), Complex(2, 2), Complex(0, 3));
cout << t << endl;
cout << "Area: " << t.area() << endl;
// change the points of the Triangle_Complex
cin >> t;
cout << t << endl;
cout << "Area: " << t.area() << endl;
return 0;
}
Example 3: Complex Number & Triangles
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
using namespace std;
class Triangle_Complex; // forward declaration
class Integer
{
protected:
int m_int_value;
public:
Integer(int arg_int_value = 0) : m_int_value(arg_int_value)
{
}
Integer(const Integer &arg_int) : m_int_value(arg_int.m_int_value)
{
}
operator int() const
{
return m_int_value;
}
Integer &operator=(const Integer &arg_int)
{
m_int_value = arg_int.m_int_value;
return *this;
}
void set_int_value(int arg_int_value)
{
m_int_value = arg_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Integer &arg_integer)
{
arg_os << arg_integer.m_int_value;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Integer &arg_integer)
{
arg_is >> arg_integer.m_int_value;
return arg_is;
}
friend Integer operator+(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value + arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator-(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value - arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator*(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value * arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator/(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value / arg_integer2.m_int_value);
return temp_integer;
}
};
// Real is a Integer
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value = 0.0) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
Real(const Real &arg_real) : Integer(arg_real),
m_after_decimal(arg_real.m_after_decimal)
{
}
operator double() const
{
return m_after_decimal + (double)m_int_value;
}
Real &operator=(const Real &arg_real)
{
m_int_value = arg_real.m_int_value;
m_after_decimal = arg_real.m_after_decimal;
return *this;
}
void set_real_value(double arg_value)
{
m_int_value = (int)arg_value;
m_after_decimal = arg_value - m_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Real &arg_real)
{
arg_os << (double)arg_real;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Real &arg_real)
{
double temp_double;
arg_is >> temp_double;
arg_real.set_real_value(temp_double);
return arg_is;
}
friend Real operator+(const Real &arg_real1, const Real &arg_real2)
{
// call the Integer operator+ to add the Integer part
Integer temp_integer((Integer)arg_real1 + (Integer)arg_real2);
Real temp_real(arg_real1.m_after_decimal + arg_real2.m_after_decimal);
temp_real.set_int_value((int)temp_integer + (int)temp_real);
return temp_real;
}
friend Real operator-(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 - (double)arg_real2);
return temp_real;
}
friend Real operator*(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 * (double)arg_real2);
return temp_real;
}
friend Real operator/(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 / (double)arg_real2);
return temp_real;
}
};
class Imaginary
{
protected:
double m_imaginary_value;
public:
Imaginary(double arg_imaginary_value = 0.0) : m_imaginary_value(arg_imaginary_value)
{
}
Imaginary(const Imaginary &arg_imaginary) : m_imaginary_value(arg_imaginary.m_imaginary_value)
{
}
Imaginary &operator=(const Imaginary &arg_imaginary)
{
m_imaginary_value = arg_imaginary.m_imaginary_value;
return *this;
}
double get_imaginary_value() const
{
return m_imaginary_value;
}
void set_imaginary_value(double arg_imaginary_value)
{
m_imaginary_value = arg_imaginary_value;
}
friend ostream &operator<<(ostream &arg_os, const Imaginary &arg_imaginary)
{
arg_os << arg_imaginary.m_imaginary_value << "i";
return arg_os;
}
friend Imaginary operator+(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value + arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
friend Imaginary operator-(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value - arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
};
class Complex : public Real, public Imaginary
{
public:
Complex(double arg_real_value = 0.0,
double arg_imaginary_value = 0.0)
: Real(arg_real_value),
Imaginary(arg_imaginary_value)
{
}
Complex(const Complex &arg_complex)
: Real(arg_complex),
Imaginary(arg_complex)
{
}
Complex &operator=(const Complex &arg_complex)
{
Real::operator=(arg_complex);
Imaginary::operator=(arg_complex);
return *this;
}
Complex reciprocal() const
{
Complex temp_complex(*this);
double temp_real_value = temp_complex;
double temp_imaginary_value = temp_complex.get_imaginary_value();
double temp_denominator = temp_real_value * temp_real_value + temp_imaginary_value * temp_imaginary_value;
temp_complex.set_real_value(temp_real_value / temp_denominator);
temp_complex.set_imaginary_value(-temp_imaginary_value / temp_denominator);
return temp_complex;
}
double get_magnitude() const
{
Real temp_real(*this);
return sqrt((double)(temp_real * temp_real) + get_imaginary_value() * get_imaginary_value());
}
Complex get_argument() const
{
double magnitude = get_magnitude();
Complex temp_complex((double)(*this) / magnitude, get_imaginary_value() / magnitude);
return temp_complex;
}
friend ostream &operator<<(ostream &arg_os, const Complex &arg_complex)
{
arg_os << (Real)arg_complex << " + " << (Imaginary)arg_complex;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Complex &arg_complex)
{
string temp_string;
getline(arg_is, temp_string, '+');
arg_complex.set_real_value(stod(temp_string));
getline(arg_is, temp_string, 'i');
arg_complex.set_imaginary_value(stod(temp_string));
return arg_is;
}
friend Complex operator+(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 + (double)arg_complex2,
arg_complex1.get_imaginary_value() + arg_complex2.get_imaginary_value());
return temp_complex;
}
friend Complex operator-(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 - (double)arg_complex2,
arg_complex1.get_imaginary_value() - arg_complex2.get_imaginary_value());
return temp_complex;
}
friend Complex operator*(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 * (double)arg_complex2 -
arg_complex1.get_imaginary_value() * arg_complex2.get_imaginary_value(),
(double)arg_complex1 * arg_complex2.get_imaginary_value() +
arg_complex1.get_imaginary_value() * (double)arg_complex2);
return temp_complex;
}
friend Complex operator/(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex(arg_complex1 * arg_complex2.reciprocal());
return temp_complex;
}
friend bool operator==(const Complex &arg_complex1, const Complex &arg_complex2)
{
return ((double)arg_complex1 == (double)arg_complex2) &&
(arg_complex1.get_imaginary_value() == arg_complex2.get_imaginary_value());
}
friend bool operator!=(const Complex &arg_complex1, const Complex &arg_complex2)
{
return !(arg_complex1 == arg_complex2);
}
friend bool operator<(const Complex &arg_complex1, const Complex &arg_complex2)
{
return ((double)arg_complex1 < (double)arg_complex2) ||
((double)arg_complex1 == (double)arg_complex2 &&
arg_complex1.get_imaginary_value() < arg_complex2.get_imaginary_value());
}
friend bool operator>(const Complex &arg_complex1, const Complex &arg_complex2)
{
return arg_complex2 < arg_complex1;
}
friend bool operator<=(const Complex &arg_complex1, const Complex &arg_complex2)
{
return !(arg_complex1 > arg_complex2);
}
friend bool operator>=(const Complex &arg_complex1, const Complex &arg_complex2)
{
return !(arg_complex1 < arg_complex2);
}
friend class Triangle_Complex;
};
// Triangle_Complex class declaration
class Triangle_Complex
{
protected:
// define three points of the Triangle_Complex
// Triangle 'has-a' Complex, so it use composition
Complex m_point[3];
// check & correct the Triangle_Complex points to counterclockwise order
void _check_points()
{
// if the area is negative, swap the points
if (area() < 0.0)
{
Complex temp = m_point[0];
m_point[0] = m_point[1];
m_point[1] = temp;
}
}
public:
// Constructor
Triangle_Complex(const Complex &arg_point1,
const Complex &arg_point2,
const Complex &arg_point3)
: m_point{arg_point1, arg_point2, arg_point3}
{
_check_points();
}
// Copy constructor
Triangle_Complex(const Triangle_Complex &arg_triangle)
: m_point{arg_triangle.m_point[0], arg_triangle.m_point[1], arg_triangle.m_point[2]}
{
}
// Destructor
~Triangle_Complex() {} // do nothing
// modify the three points of the Triangle_Complex
void set_points(const Complex &arg_point1,
const Complex &arg_point2,
const Complex &arg_point3)
{
m_point[0] = arg_point1;
m_point[1] = arg_point2;
m_point[2] = arg_point3;
_check_points();
}
void set_point1(const Complex &arg_point1)
{
m_point[0] = arg_point1;
_check_points();
}
void set_point2(const Complex &arg_point2)
{
m_point[1] = arg_point2;
_check_points();
}
void set_point3(const Complex &arg_point3)
{
m_point[2] = arg_point3;
_check_points();
}
// get the three points of the Triangle_Complex
Complex get_point1() const
{
return m_point[0];
}
Complex get_point2() const
{
return m_point[1];
}
Complex get_point3() const
{
return m_point[2];
}
// calculate the area of the Triangle_Complex
double area()
{
double area = 0.0;
for (int i = 0; i < 3; i++)
{
area += (double)m_point[i] * m_point[(i + 1) % 3].get_imaginary_value();
area -= m_point[i].get_imaginary_value() * (double)m_point[(i + 1) % 3];
}
return area / 2.0;
}
// print the Triangle_Complex
// format: (c1, c2, c3)
friend std::ostream &operator<<(std::ostream &arg_os, const Triangle_Complex &arg_tri)
{
arg_os << "(";
for (int i = 0; i < 3; i++)
{
arg_os << arg_tri.m_point[i];
if (i < 2)
arg_os << ", ";
}
arg_os << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: (c1, c2, c3) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Triangle_Complex &arg_tri)
{
string temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
for (int i = 0; i < 3; i++)
{
arg_is >> arg_tri.m_point[i];
if (i < 2)
{
getline(arg_is, temp, ','); // ignore the ','
}
}
getline(arg_is, temp, ')'); // ignore the last ')'
}
// check & correct the Triangle_Complex points to counterclockwise order
arg_tri._check_points();
return arg_is;
}
};
class Equilateral_Triangle_Complex : public Triangle_Complex
// Equilateral Triangle `is-a' Triangle_Complex, so it use inheritance
// use function overloading to implement the different function
// of Equilateral_Triangle_Complex
// details will be discussed in polymorphism (next chapter)
{
public:
Equilateral_Triangle_Complex(const Complex &arg_point1,
const Complex &arg_point2)
: Triangle_Complex(arg_point1, arg_point2, arg_point1)
{
Complex temp = arg_point2 - arg_point1;
temp = temp * Complex(0.5, sqrt(3.0) / 2.0); // rotate 60 degree
m_point[2] = arg_point1 + temp; // calculate the third point
_check_points();
}
void set_points(const Complex &arg_point1,
const Complex &arg_point2)
{
m_point[0] = arg_point1;
m_point[1] = arg_point2;
Complex temp = arg_point2 - arg_point1;
temp = temp * Complex(0.5, sqrt(3.0) / 2.0); // rotate 60 degree
m_point[2] = arg_point1 + temp; // calculate the third point
_check_points();
}
void set_point1(const Complex &arg_point1)
{
// invalid operation
}
void set_point2(const Complex &arg_point2)
{
// invalid operation
}
void set_point3(const Complex &arg_point3)
{
// invalid operation
}
// read the coordinate of a point from the input,
// format: (c1, c2, c3) and ignore c3 and spaces
friend std::istream &operator>>(std::istream &arg_is,
Equilateral_Triangle_Complex &arg_tri)
{
string temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
for (int i = 0; i < 3; i++)
{
if (i < 2)
{
arg_is >> arg_tri.m_point[i];
getline(arg_is, temp, ','); // ignore the ','
}
}
getline(arg_is, temp, ')'); // ignore the c3 and last ')'
}
// check & correct the Triangle_Complex points to counterclockwise order
arg_tri._check_points();
return arg_is;
}
};
// main function
int main()
{
Equilateral_Triangle_Complex t(Complex(1, 1), Complex(2, 2));
cout << t << endl;
cout << "Area: " << t.area() << endl;
// change the points of the Triangle_Complex
cin >> t;
cout << t << endl;
cout << "Area: " << t.area() << endl;
return 0;
}
OOP: Polymorphism (1)
Slides version: lecture11_slides.html Website version: lecture11.html
- What is Polymorphism? and Why do we need it?
- Example: Bus, Car, and Truck.
- Polymorphism Types
- Compile time
- Run time
- Virtual Function
- Syntax:
virtualmember function & object pointer - Example:
- Syntax:
- Example 1: Integer & Real
- Example 2: Complex Number
- Example 3: Integer & Real & Complex Number
- Pratices
What is Polymorphism? and Why do we need it?
Ref: https://www.geeksforgeeks.org/polymorphism-in-c/
The word polymorphism means having many forms. In simple words, we can define polymorphism as the ability of a message to be displayed in more than one form. A real-life example of polymorphism, a person at the same time can have different characteristics. Like a man at the same time is a father, a husband, an employee. So the same person posses different behavior in different situations. This is called polymorphism.
Example: Bus, Car, and Truck
- A Bus:
- has 4 wheels
- has 20 seats
- has 2 doors
- has 20 windows
- A Car:
- has 4 wheels
- has 4 seats
- has 4 doors
- has 4 windows
- A Truck:
- has 6 wheels
- has 2 seats
- has 2 doors
- has 2 windows
function overloading
#include <iostream>
using namespace std;
class Vehicle
{
public:
void wheels() {}
void seats() {}
void doors() {}
void windows() {}
};
class Bus : public Vehicle
{
public:
void wheels()
{
cout << "Wheels: 4" << endl;
}
void seats()
{
cout << "Seats: 20" << endl;
}
void doors()
{
cout << "Doors: 2" << endl;
}
void windows()
{
cout << "Windows: 20" << endl;
}
};
class Car : public Vehicle
{
public:
void wheels()
{
cout << "Wheels: 4" << endl;
}
void seats()
{
cout << "Seats: 4" << endl;
}
void doors()
{
cout << "Doors: 4" << endl;
}
void windows()
{
cout << "Windows: 4" << endl;
}
};
class Truck : public Vehicle
{
public:
void wheels()
{
cout << "Wheels: 6" << endl;
}
void seats()
{
cout << "Seats: 2" << endl;
}
void doors()
{
cout << "Doors: 2" << endl;
}
void windows()
{
cout << "Windows: 2" << endl;
}
};
int main()
{
Bus b;
Car c;
Truck t;
b.wheels();
b.seats();
b.doors();
b.windows();
c.wheels();
c.seats();
c.doors();
c.windows();
t.wheels();
t.seats();
t.doors();
t.windows();
}
Output:
$ ./a.out
Wheels: 4
Seats: 20
Doors: 2
Windows: 20
Wheels: 4
Seats: 4
Doors: 4
Windows: 4
Wheels: 6
Seats: 2
Doors: 2
Windows: 2
virtual member function
#include <iostream>
using namespace std;
class Vehicle
{
public:
virtual void wheels() {}
virtual void seats() {}
virtual void doors() {}
virtual void windows() {}
};
class Bus : public Vehicle
{
public:
void wheels()
{
cout << "Wheels: 4" << endl;
}
void seats()
{
cout << "Seats: 20" << endl;
}
void doors()
{
cout << "Doors: 2" << endl;
}
void windows()
{
cout << "Windows: 20" << endl;
}
};
class Car : public Vehicle
{
public:
void wheels()
{
cout << "Wheels: 4" << endl;
}
void seats()
{
cout << "Seats: 4" << endl;
}
void doors()
{
cout << "Doors: 4" << endl;
}
void windows()
{
cout << "Windows: 4" << endl;
}
};
class Truck : public Vehicle
{
public:
void wheels()
{
cout << "Wheels: 6" << endl;
}
void seats()
{
cout << "Seats: 2" << endl;
}
void doors()
{
cout << "Doors: 2" << endl;
}
void windows()
{
cout << "Windows: 2" << endl;
}
};
int main()
{
Vehicle *v[3]; // array of pointers to Vehicle
// used for polymorphism
v[0] = new Bus; // dynamically allocate Bus
v[1] = new Car; // dynamically allocate Car
v[2] = new Truck; // dynamically allocate Truck
for (int i = 0; i < 3; i++)
{
v[i]->wheels();
v[i]->seats();
v[i]->doors();
v[i]->windows();
}
for (int i = 0; i < 3; i++)
{
delete v[i];
}
}
Output:
$ ./a.out
Wheels: 4
Seats: 20
Doors: 2
Windows: 20
Wheels: 4
Seats: 4
Doors: 4
Windows: 4
Wheels: 6
Seats: 2
Doors: 2
Windows: 2
Polymorphism Types
- In C++ polymorphism is mainly divided into two types:
- Compile time Polymorphism
- Runtime Polymorphism
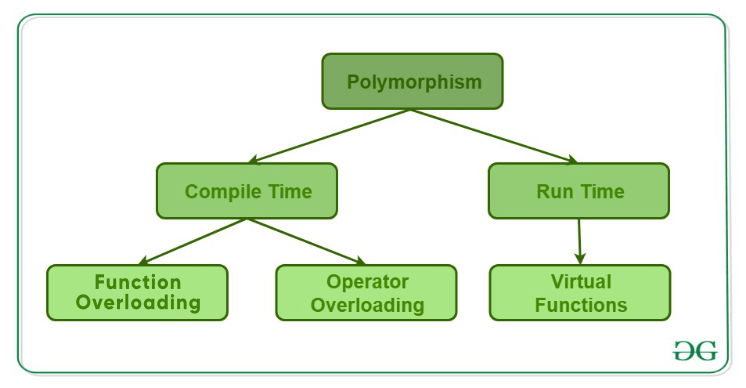
Compile time Polymorphism (Function/Operator Overloading)
// C++ program for function overloading
#include <iostream>
using namespace std;
class Geeks
{
public:
// function with 1 int parameter
void func(int x)
{
cout << "value of x is " << x << endl;
}
// function with same name but 1 double parameter
void func(double x)
{
cout << "value of x is " << x << endl;
}
// function with same name and 2 int parameters
void func(int x, int y)
{
cout << "value of x and y is " << x << ", " << y << endl;
}
};
int main()
{
Geeks obj1;
// Which function is called will depend on the parameters passed
// The first 'func' is called
obj1.func(7);
// The second 'func' is called
obj1.func(9.132);
// The third 'func' is called
obj1.func(85, 64);
return 0;
}
Runtime Polymorphism (Virtual Function with object pointer)
// C++ program for function overriding
#include <iostream>
using namespace std;
class base
{
public:
virtual void print()
{
cout << "print base class" << endl;
}
void show()
{
cout << "show base class" << endl;
}
};
class derived : public base
{
public:
void print() // print () is already virtual function in derived class,
// we could also declared as virtual void print () explicitly
{
cout << "print derived class" << endl;
}
void show()
{
cout << "show derived class" << endl;
}
};
// main function
int main()
{
base *bptr;
derived d;
bptr = &d;
// virtual function, binded at runtime (Runtime polymorphism)
bptr->print();
// Non-virtual function, binded at compile time
bptr->show();
return 0;
}
Virtual Function
Ref: https://www.geeksforgeeks.org/virtual-functions-and-runtime-polymorphism-in-c-set-1-introduction/
A virtual function is a member function which is declared in the base class using the keyword
virtualand is re-defined (Overriden) by the derived class.
Syntax: virtual member function & object pointer
class base
{
public:
virtual void a() {} // virtual function
};
class derived : public base
{
public:
void a() {} // non-virtual function, overridden by derived class
};
int main()
{
base *b_ptr;
derived d;
b_ptr = &d; // object pointer of derived class
// virtual function, binded at runtime (Runtime polymorphism)
b_ptr->a();
return 0;
}
Example 1:
// C++ program for function overriding
#include <iostream>
using namespace std;
class base
{
public:
virtual void print()
{
cout << "print base class" << endl;
}
void show()
{
cout << "show base class" << endl;
}
};
class derived : public base
{
public:
void print() // print () is already virtual function in derived class,
// we could also declared as virtual void print () explicitly
{
cout << "print derived class" << endl;
}
void show()
{
cout << "show derived class" << endl;
}
};
// main function
int main()
{
base *bptr;
derived d;
bptr = &d;
// virtual function, binded at runtime (Runtime polymorphism)
bptr->print();
// Non-virtual function, binded at compile time
bptr->show();
return 0;
}
Example 2:
class Employee
{
public:
virtual void raiseSalary()
{
/* common raise salary code */
}
virtual void promote()
{
/* common promote code */
}
};
class Manager : public Employee
{
virtual void raiseSalary()
{
/* Manager specific raise salary code, may contain
increment of manager specific incentives */
}
virtual void promote()
{
/* Manager specific promote */
}
};
// Similarly, there may be other types of employees
// We need a very simple function
// to increment the salary of all employees
// Note that emp[] is an array of pointers
// and actual pointed objects can
// be any type of employees.
// This function should ideally
// be in a class like Organization,
// we have made it global to keep things simple
void globalRaiseSalary(Employee *emp[], int n)
{
for (int i = 0; i < n; i++)
{
// Polymorphic Call: Calls raiseSalary()
// according to the actual object, not
// according to the type of pointer
emp[i]->raiseSalary();
}
}
Example 1: Integer & Real [Source]
Example 2: Complex Number [Source]
Example 3: Integer & Real & Complex Number [Source]
Pratices
-
Design a class hierarchy for Fruit.
- Contains: Grape, Apple, Orange
- Implement with based class
Fruit - Use
virtualfunction to provide universalprint(),color()functions
-
Design a class hierarchy for Quadrilateral.
- Contains: Square, Rectangle, Rhombus, Parallelogram
- Implement with based class
Quadrilateral - Use
virtualfunction to provide universalprint(),area()functions
Example 1: Integer & Real
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Number
{
public:
Number()
{
}
virtual double get_value() const
{
return 0.0;
}
virtual string get_string() const
{
return "";
}
virtual void set_value(double value)
{
}
};
class Integer : public Number
{
protected:
int m_int_value;
public:
Integer(int arg_int_value = 0) : m_int_value(arg_int_value)
{
}
Integer(const Integer &arg_int) : m_int_value(arg_int.m_int_value)
{
}
operator int() const
{
return m_int_value;
}
operator double() const
{
return (double)m_int_value;
}
double get_value() const
{
return (double)m_int_value;
}
string get_string() const
{
return to_string(m_int_value);
}
Integer &operator=(const Integer &arg_int)
{
m_int_value = arg_int.m_int_value;
return *this;
}
void set_value(int arg_int_value) // int version
{
m_int_value = arg_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Integer &arg_integer)
{
arg_os << arg_integer.get_string();
return arg_os;
}
friend istream &operator>>(istream &arg_is, Integer &arg_integer)
{
arg_is >> arg_integer.m_int_value;
return arg_is;
}
};
// Real is a Integer
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value = 0.0) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
Real(const Real &arg_real) : Integer(arg_real),
m_after_decimal(arg_real.m_after_decimal)
{
}
operator double() const
{
return m_after_decimal + (double)m_int_value;
}
double get_value() const
{
return m_after_decimal + (double)m_int_value;
}
string get_string() const
{
return to_string(Real::get_value());
}
Real &operator=(const Real &arg_real)
{
m_int_value = arg_real.m_int_value;
m_after_decimal = arg_real.m_after_decimal;
return *this;
}
void set_value(double arg_value) // double version
{
m_int_value = (int)arg_value;
m_after_decimal = arg_value - m_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Real &arg_real)
{
arg_os << (double)arg_real;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Real &arg_real)
{
double temp_double;
arg_is >> temp_double;
arg_real.set_value(temp_double);
return arg_is;
}
};
int main()
{
Number *p[2];
p[0] = new Integer(10);
p[1] = new Real(10.5);
cout << "virtual function call" << endl;
for (int i = 0; i < 2; i++)
{
cout << "p[" << i << "] = " << p[i]->get_string() << endl;
}
cout << "address of object" << endl;
for (int i = 0; i < 2; i++)
{
cout << "p[" << i << "] = " << p[i] << endl;
}
for (int i = 0; i < 2; i++)
{
delete p[i];
}
}
Example 2: Complex Number
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Number
{
public:
Number()
{
}
virtual double get_value() const
{
return 0.0;
}
virtual string get_string() const
{
return "";
}
virtual void set_value(string arg_s)
{
}
};
class Integer : public Number
{
protected:
int m_int_value;
public:
Integer(int arg_int_value = 0) : m_int_value(arg_int_value)
{
}
Integer(const Integer &arg_int) : m_int_value(arg_int.m_int_value)
{
}
operator int() const
{
return m_int_value;
}
operator double() const
{
return (double)m_int_value;
}
double get_value() const
{
return (double)m_int_value;
}
string get_string() const
{
return to_string(m_int_value);
}
Integer &operator=(const Integer &arg_int)
{
m_int_value = arg_int.m_int_value;
return *this;
}
void set_value(string arg_int_value) // int version
{
stringstream ss(arg_int_value); // use operator>> to convert string to Integer
ss >> m_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Integer &arg_integer)
{
arg_os << arg_integer.get_string();
return arg_os;
}
friend istream &operator>>(istream &arg_is, Integer &arg_integer)
{
arg_is >> arg_integer.m_int_value;
return arg_is;
}
};
// Real is a Integer
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value = 0.0) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
Real(const Real &arg_real) : Integer(arg_real),
m_after_decimal(arg_real.m_after_decimal)
{
}
operator double() const
{
return m_after_decimal + (double)m_int_value;
}
double get_value() const
{
return m_after_decimal + (double)m_int_value;
}
string get_string() const
{
return to_string(Real::get_value());
}
Real &operator=(const Real &arg_real)
{
m_int_value = arg_real.m_int_value;
m_after_decimal = arg_real.m_after_decimal;
return *this;
}
void set_value(string arg_value) // double version
{
double temp_double;
temp_double = stod(arg_value);
m_int_value = (int)temp_double;
m_after_decimal = temp_double - (double)m_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Real &arg_real)
{
arg_os << (double)arg_real;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Real &arg_real)
{
string temp_string;
arg_is >> temp_string;
arg_real.set_value(temp_string);
return arg_is;
}
};
class Complex : public Real
{
private:
Real m_imaginary;
public:
Complex(double arg_real_value = 0.0,
double arg_imaginary_value = 0.0)
: Real(arg_real_value),
m_imaginary(arg_imaginary_value)
{
}
Complex(const Complex &arg_complex)
: Real(arg_complex),
m_imaginary(arg_complex.m_imaginary)
{
}
double get_value() const
{
cout << "not implemented" << endl;
return 0.0;
}
string get_string() const
{
return to_string((double)*this) + " + " + m_imaginary.get_string() + "i";
}
Complex &operator=(const Complex &arg_complex)
{
Real::operator=(arg_complex);
m_imaginary = arg_complex.m_imaginary;
return *this;
}
void set_value(string arg_value) // complex version
{
size_t plus_pos = arg_value.find("+");
if (plus_pos != string::npos)
{
Real::set_value(arg_value.substr(0, plus_pos));
}
size_t i_pos = arg_value.find("i");
if (i_pos != string::npos)
{
m_imaginary.set_value(arg_value.substr(plus_pos + 1, i_pos - plus_pos - 1));
}
}
friend ostream &operator<<(ostream &arg_os, const Complex &arg_complex)
{
arg_os << arg_complex.get_string();
return arg_os;
}
friend istream &operator>>(istream &arg_is, Complex &arg_complex)
{
string temp_string;
getline(arg_is, temp_string);
arg_complex.set_value(temp_string);
return arg_is;
}
};
int main()
{
Number *p[3];
p[0] = new Integer(10);
p[1] = new Real(10.5);
p[2] = new Complex(10.5, 3.5);
cout << "virtual function call" << endl;
for (int i = 0; i < 3; i++)
{
cout << "p[" << i << "] = " << p[i]->get_string() << endl;
}
cout << "address of object" << endl;
for (int i = 0; i < 3; i++)
{
cout << "p[" << i << "] = " << p[i] << endl;
}
p[0]->set_value("20");
p[1]->set_value("20.5");
p[2]->set_value("20.5 + 3.5i");
cout << "set value by virtual function" << endl;
for (int i = 0; i < 3; i++)
{
cout << "p[" << i << "] = " << p[i]->get_string() << endl;
}
for (int i = 0; i < 3; i++)
{
delete p[i];
}
}
Example 3: Integer & Real & Complex Number
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
class Number
{
public:
Number()
{
}
virtual double get_value() const
{
return 0.0;
}
virtual string get_string() const
{
return "";
}
virtual void set_value(string arg_s)
{
}
};
class Integer : public Number
{
protected:
int m_int_value;
public:
Integer(int arg_int_value = 0) : m_int_value(arg_int_value)
{
}
Integer(const Integer &arg_int) : m_int_value(arg_int.m_int_value)
{
}
operator int() const
{
return m_int_value;
}
operator double() const
{
return (double)m_int_value;
}
double get_value() const
{
return (double)m_int_value;
}
string get_string() const
{
return to_string(m_int_value);
}
Integer &operator=(const Integer &arg_int)
{
m_int_value = arg_int.m_int_value;
return *this;
}
void set_value(string arg_int_value) // int version
{
stringstream ss(arg_int_value); // use operator>> to convert string to Integer
ss >> m_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Integer &arg_integer)
{
arg_os << arg_integer.get_string();
return arg_os;
}
friend istream &operator>>(istream &arg_is, Integer &arg_integer)
{
arg_is >> arg_integer.m_int_value;
return arg_is;
}
};
// Real is a Integer
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value = 0.0) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
Real(const Real &arg_real) : Integer(arg_real),
m_after_decimal(arg_real.m_after_decimal)
{
}
operator double() const
{
return m_after_decimal + (double)m_int_value;
}
double get_value() const
{
return m_after_decimal + (double)m_int_value;
}
string get_string() const
{
return to_string(Real::get_value());
}
Real &operator=(const Real &arg_real)
{
m_int_value = arg_real.m_int_value;
m_after_decimal = arg_real.m_after_decimal;
return *this;
}
void set_value(string arg_value) // double version
{
double temp_double;
temp_double = stod(arg_value);
m_int_value = (int)temp_double;
m_after_decimal = temp_double - (double)m_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Real &arg_real)
{
arg_os << (double)arg_real;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Real &arg_real)
{
string temp_string;
arg_is >> temp_string;
arg_real.set_value(temp_string);
return arg_is;
}
};
class Imaginary
{
protected:
double m_imaginary_value;
public:
Imaginary(double arg_imaginary_value = 0.0) : m_imaginary_value(arg_imaginary_value)
{
}
Imaginary(const Imaginary &arg_imaginary) : m_imaginary_value(arg_imaginary.m_imaginary_value)
{
}
Imaginary &operator=(const Imaginary &arg_imaginary)
{
m_imaginary_value = arg_imaginary.m_imaginary_value;
return *this;
}
double get_value() const // use the same function as Number to
// maintain the same interface
{
return m_imaginary_value;
}
string get_string() const
{
return to_string(m_imaginary_value) + "i";
}
void set_value(string arg_imaginary_value)
{
m_imaginary_value = stod(arg_imaginary_value);
}
friend ostream &operator<<(ostream &arg_os, const Imaginary &arg_imaginary)
{
arg_os << arg_imaginary.get_string();
return arg_os;
}
};
class Complex : public Real, public Imaginary
{
public:
Complex(double arg_real_value = 0.0,
double arg_imaginary_value = 0.0)
: Real(arg_real_value),
Imaginary(arg_imaginary_value)
{
}
Complex(const Complex &arg_complex)
: Real(arg_complex),
Imaginary(arg_complex)
{
}
double get_value() const
{
cout << "not implemented" << endl;
return 0.0;
}
string get_string() const
{
return Real::get_string() + " + " + Imaginary::get_string();
}
Complex &operator=(const Complex &arg_complex)
{
Real::operator=(arg_complex);
Imaginary::operator=(arg_complex);
return *this;
}
void set_value(string arg_value) // complex version
{
size_t plus_pos = arg_value.find("+");
if (plus_pos != string::npos)
{
Real::set_value(arg_value.substr(0, plus_pos));
}
size_t i_pos = arg_value.find("i");
if (i_pos != string::npos)
{
Imaginary::set_value(arg_value.substr(plus_pos + 1, i_pos - plus_pos - 1));
}
}
friend ostream &operator<<(ostream &arg_os, const Complex &arg_complex)
{
arg_os << arg_complex.get_string();
return arg_os;
}
friend istream &operator>>(istream &arg_is, Complex &arg_complex)
{
string temp_string;
getline(arg_is, temp_string);
arg_complex.set_value(temp_string);
return arg_is;
}
};
int main()
{
Number *p[3];
p[0] = new Integer(10);
p[1] = new Real(10.5);
p[2] = new Complex(10.5, 3.5);
cout << "virtual function call" << endl;
for (int i = 0; i < 3; i++)
{
cout << "p[" << i << "] = " << p[i]->get_string() << endl;
}
cout << "address of object" << endl;
for (int i = 0; i < 3; i++)
{
cout << "p[" << i << "] = " << p[i] << endl;
}
p[0]->set_value("20");
p[1]->set_value("20.5");
p[2]->set_value("20.5 + 3.5i");
cout << "set value by virtual function" << endl;
for (int i = 0; i < 3; i++)
{
cout << "p[" << i << "] = " << p[i]->get_string() << endl;
}
for (int i = 0; i < 3; i++)
{
delete p[i];
}
}
OOP: Polymorphism (2)
Slides version: lecture12_slides.html Website version: lecture12.html
- Recap Polymorphism
- Example: Bus, Car, and Truck.
- Polymorphism Types
- Compile time, Run time
- Pointer to Polymorphic Objects
- What is a pointer? and how to use it?
- How a pointer to a polymorphic object works? (Late binding)
- Polymorphism in Software Engineering
- Pros & Cons
- Compile time & Run time
- Example 1: Integer & Real & Complex Number Calculator
- Example 2: Complex Number & Triangles
- Lab 6: Complex Number Calculator
Recap Polymorphism
Example: Bus, Car, and Truck
- A Bus:
- has 4 wheels
- has 20 seats
- has 2 doors
- has 20 windows
- A Car:
- has 4 wheels
- has 4 seats
- has 4 doors
- has 4 windows
- A Truck:
- has 6 wheels
- has 2 seats
- has 2 doors
- has 2 windows
Polymorphism Types
- In C++ polymorphism is mainly divided into two types:
- Compile time Polymorphism
- Runtime Polymorphism

Compile time Polymorphism (Function/Operator Overloading)
// C++ program for function overloading
#include <iostream>
using namespace std;
class Geeks
{
public:
// function with 1 int parameter
void func(int x)
{
cout << "value of x is " << x << endl;
}
// function with same name but 1 double parameter
void func(double x)
{
cout << "value of x is " << x << endl;
}
// function with same name and 2 int parameters
void func(int x, int y)
{
cout << "value of x and y is " << x << ", " << y << endl;
}
};
int main()
{
Geeks obj1;
// Which function is called will depend on the parameters passed
// The first 'func' is called
obj1.func(7);
// The second 'func' is called
obj1.func(9.132);
// The third 'func' is called
obj1.func(85, 64);
return 0;
}
Runtime Polymorphism (Virtual Function with object pointer)
// C++ program for function overriding
#include <iostream>
using namespace std;
class base
{
public:
virtual void print()
{
cout << "print base class" << endl;
}
void show()
{
cout << "show base class" << endl;
}
};
class derived : public base
{
public:
void print() // print () is already virtual function in derived class,
// we could also declared as virtual void print () explicitly
{
cout << "print derived class" << endl;
}
void show()
{
cout << "show derived class" << endl;
}
};
// main function
int main()
{
base *bptr;
derived d;
bptr = &d;
// virtual function, binded at runtime (Runtime polymorphism)
bptr->print();
// Non-virtual function, binded at compile time
bptr->show();
return 0;
}
Pointer to Polymorphic Objects
Consider the example:
// CPP program to illustrate
// working of Virtual Functions
#include <iostream>
using namespace std;
class base
{
public:
void fun_1() { cout << "base-1\n"; }
virtual void fun_2() { cout << "base-2\n"; }
virtual void fun_3() { cout << "base-3\n"; }
virtual void fun_4() { cout << "base-4\n"; }
};
class derived : public base
{
public:
void fun_1() { cout << "derived-1\n"; }
void fun_2() { cout << "derived-2\n"; }
void fun_4(int x) { cout << "derived-4\n"; }
};

What is a pointer? and how to use it?
Ref: Pointer in C++
Pointers store address of variables or a memory location.

Example: Pointer
// C++ program to demonstrate use of * for pointers in C++
#include <iostream>
using namespace std;
int main()
{
// A normal integer variable
int Var = 10;
// A pointer variable that holds address of var.
int *ptr = &Var;
// This line prints value at address stored in ptr.
// Value stored is value of variable "var"
cout << "Value of Var = " << *ptr << endl;
// The output of this line may be different in different
// runs even on same machine.
cout << "Address of Var = " << ptr << endl;
// We can also use ptr as lvalue (Left hand
// side of assignment)
*ptr = 20; // Value at address is now 20
// This prints 20
cout << "After doing *ptr = 20, *ptr is " << *ptr << endl;
return 0;
}
// This code is contributed by
// shubhamsingh10
Output:
Value of Var = 10
Address of Var = 0x7fffa057dd4
After doing *ptr = 20, *ptr is 20
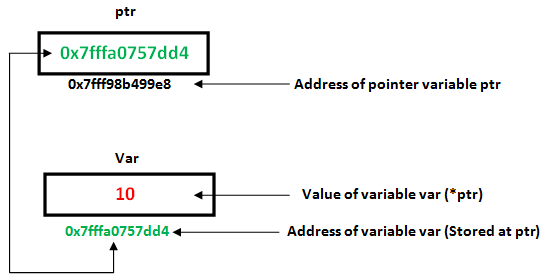
How a pointer to a polymorphic object works? (Late binding)
Ref: Virtual Functions and Runtime Polymorphism in C++

The compiler maintains two things to serve this purpose:
- vtable: A table of function pointers, maintained per class.
- vptr: A pointer to vtable, maintained per object instance.
Consider the example:
// CPP program to illustrate
// working of Virtual Functions
#include <iostream>
using namespace std;
class base
{
public:
void fun_1() { cout << "base-1\n"; }
virtual void fun_2() { cout << "base-2\n"; }
virtual void fun_3() { cout << "base-3\n"; }
virtual void fun_4() { cout << "base-4\n"; }
};
class derived : public base
{
public:
void fun_1() { cout << "derived-1\n"; }
void fun_2() { cout << "derived-2\n"; }
void fun_4(int x) { cout << "derived-4\n"; }
};

On the runtime:
int main()
{
base *p;
derived obj1;
p = &obj1;
// Early binding because fun1() is non-virtual
// in base
p->fun_1();
// Late binding (RTP)
p->fun_2();
// Late binding (RTP)
p->fun_3();
// Late binding (RTP)
p->fun_4();
// Early binding but this function call is
// illegal (produces error) because pointer
// is of base type and function is of
// derived class
// p->fun_4(5);
return 0;
}
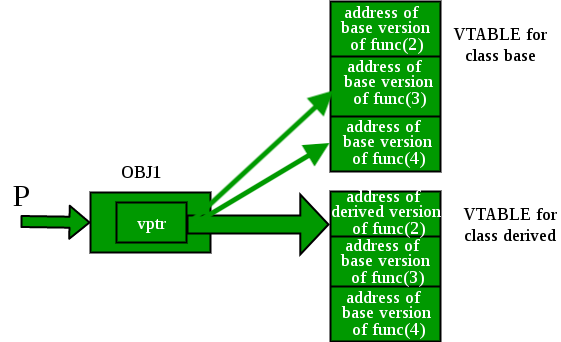
Polymorphism in Software Engineering
Ref: https://en.wikipedia.org/wiki/Polymorphism_(computer_science)
Polymorphism is the provision of a single interface to entities of different types1 or the use of a single symbol to represent multiple different types.2 The concept is borrowed from a principle in biology where an organism or species can have many different forms or stages.3
Pros & Cons of Polymorphism
Pros
- Reuse codes with various types of objects.
- Use the same code/interface to work with different types of objects.
- Use functions when the application is running.
Cons
One of the disadvantages of polymorphism is that developers find it difficult to implement polymorphism in codes. Run time polymorphism can lead to the performance issue as machine needs to decide which method or variable to invoke so it basically degrades the performances as decisions are taken at run time. Polymorphism reduces the readability of the program. One needs to identify the runtime behavior of the program to identify actual execution time.
Ref: Akanksha Patel
Compile time & Run time Polymorphism
Difference between compile time and run time polymorphism:
Static polymorphism produces faster code, mostly because of the possibility of aggressive inlining. Virtual functions can rarely be inlined, and mostly in a "non-polymorphic" scenarios. ... On the other hand, not only compile times, but also the readability and debuggability of the code is much worse when using static polymorphism. For instance: abstract methods are a clean way of enforcing implementation of certain interface methods. ...
Ref: maciek gajewski
Example 1: Integer & Real & Complex Number Calculator [Source]
Example 2: Complex Number & Triangles [Source]
Lab 12: Complex Number's Geometry & Operations
Example 1: Integer & Real & Complex Number Calculator
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
using namespace std;
class Number
{
public:
Number()
{
}
virtual double get_value() const
{
return 0.0;
}
virtual string get_string() const
{
return "";
}
virtual void set_value(string arg_s)
{
}
virtual void add_assign(string arg_s)
{
}
virtual void sub_assign(string arg_s)
{
}
virtual void mul_assign(string arg_s)
{
}
virtual void div_assign(string arg_s)
{
}
};
class Integer : public Number
{
protected:
int m_int_value;
public:
Integer(int arg_int_value = 0) : m_int_value(arg_int_value)
{
}
Integer(const Integer &arg_int) : m_int_value(arg_int.m_int_value)
{
}
operator int() const
{
return m_int_value;
}
Integer &operator=(const Integer &arg_int)
{
m_int_value = arg_int.m_int_value;
return *this;
}
double get_value() const
{
return (double)m_int_value;
}
string get_string() const
{
return to_string(m_int_value);
}
void set_value(string arg_int_value) // int version
{
stringstream ss(arg_int_value); // use operator>> to convert string to Integer
ss >> m_int_value;
}
void add_assign(string arg_int_value) // int version
{
Integer num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 + num2;
}
void sub_assign(string arg_int_value) // int version
{
Integer num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 - num2;
}
void mul_assign(string arg_int_value) // int version
{
Integer num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 * num2;
}
void div_assign(string arg_int_value) // int version
{
Integer num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 / num2;
}
friend ostream &operator<<(ostream &arg_os, const Integer &arg_integer)
{
arg_os << arg_integer.get_string();
return arg_os;
}
friend istream &operator>>(istream &arg_is, Integer &arg_integer)
{
arg_is >> arg_integer.m_int_value;
return arg_is;
}
friend Integer operator+(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value + arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator-(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value - arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator*(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value * arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator/(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value / arg_integer2.m_int_value);
return temp_integer;
}
};
// Real is a Integer
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value = 0.0) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
Real(const Real &arg_real) : Integer(arg_real),
m_after_decimal(arg_real.m_after_decimal)
{
}
operator double() const
{
return m_after_decimal + (double)m_int_value;
}
Real &operator=(const Real &arg_real)
{
m_int_value = arg_real.m_int_value;
m_after_decimal = arg_real.m_after_decimal;
return *this;
}
double get_value() const
{
return m_after_decimal + (double)m_int_value;
}
string get_string() const
{
return to_string(Real::get_value());
}
void set_value(string arg_value) // double version
{
double temp_double;
temp_double = stod(arg_value);
m_int_value = (int)temp_double;
m_after_decimal = temp_double - (double)m_int_value;
}
void add_assign(string arg_int_value) // int version
{
Real num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 + num2;
}
void sub_assign(string arg_int_value) // int version
{
Real num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 - num2;
}
void mul_assign(string arg_int_value) // int version
{
Real num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 * num2;
}
void div_assign(string arg_int_value) // int version
{
Real num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 / num2;
}
friend ostream &operator<<(ostream &arg_os, const Real &arg_real)
{
arg_os << (double)arg_real;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Real &arg_real)
{
string temp_string;
arg_is >> temp_string;
arg_real.set_value(temp_string);
return arg_is;
}
friend Real operator+(const Real &arg_real1, const Real &arg_real2)
{
// call the Integer operator+ to add the Integer part
Integer temp_integer((Integer)arg_real1 + (Integer)arg_real2);
Real temp_real(arg_real1.m_after_decimal + arg_real2.m_after_decimal);
temp_real.set_value(to_string(temp_integer.get_value() + temp_real.get_value()));
return temp_real;
}
friend Real operator-(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 - (double)arg_real2);
return temp_real;
}
friend Real operator*(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 * (double)arg_real2);
return temp_real;
}
friend Real operator/(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 / (double)arg_real2);
return temp_real;
}
};
class Imaginary
{
protected:
double m_imaginary_value;
public:
Imaginary(double arg_imaginary_value = 0.0) : m_imaginary_value(arg_imaginary_value)
{
}
Imaginary(const Imaginary &arg_imaginary) : m_imaginary_value(arg_imaginary.m_imaginary_value)
{
}
Imaginary &operator=(const Imaginary &arg_imaginary)
{
m_imaginary_value = arg_imaginary.m_imaginary_value;
return *this;
}
double get_value() const // use the same function as Number to
// maintain the same interface
{
return m_imaginary_value;
}
string get_string() const
{
return to_string(m_imaginary_value) + "i";
}
void set_value(string arg_imaginary_value)
{
m_imaginary_value = stod(arg_imaginary_value);
}
friend ostream &operator<<(ostream &arg_os, const Imaginary &arg_imaginary)
{
arg_os << arg_imaginary.get_string();
return arg_os;
}
friend Imaginary operator+(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value + arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
friend Imaginary operator-(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value - arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
};
class Complex : public Real, public Imaginary
{
public:
Complex(double arg_real_value = 0.0,
double arg_imaginary_value = 0.0)
: Real(arg_real_value),
Imaginary(arg_imaginary_value)
{
}
Complex(const Complex &arg_complex)
: Real(arg_complex),
Imaginary(arg_complex)
{
}
Complex &operator=(const Complex &arg_complex)
{
Real::operator=(arg_complex);
Imaginary::operator=(arg_complex);
return *this;
}
double get_value() const
{
cout << "not implemented" << endl;
return 0.0;
}
string get_string() const
{
return Real::get_string() + " + " + Imaginary::get_string();
}
void set_value(string arg_value) // complex version
{
size_t plus_pos = arg_value.find("+");
if (plus_pos != string::npos)
{
Real::set_value(arg_value.substr(0, plus_pos));
}
size_t i_pos = arg_value.find("i");
if (i_pos != string::npos)
{
Imaginary::set_value(arg_value.substr(plus_pos + 1, i_pos - plus_pos - 1));
}
}
Complex reciprocal() const
{
double temp_real_value = Real::get_value();
double temp_imaginary_value = Imaginary::get_value();
double temp_denominator = temp_real_value * temp_real_value + temp_imaginary_value * temp_imaginary_value;
Complex temp_complex(temp_real_value / temp_denominator, -temp_imaginary_value / temp_denominator);
return temp_complex;
}
void add_assign(string arg_int_value) // int version
{
Complex num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 + num2;
}
void sub_assign(string arg_int_value) // int version
{
Complex num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 - num2;
}
void mul_assign(string arg_int_value) // int version
{
Complex num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 * num2;
}
void div_assign(string arg_int_value) // int version
{
Complex num1(*this), num2;
num2.set_value(arg_int_value);
*this = num1 / num2;
}
friend ostream &operator<<(ostream &arg_os, const Complex &arg_complex)
{
arg_os << arg_complex.get_string();
return arg_os;
}
friend istream &operator>>(istream &arg_is, Complex &arg_complex)
{
string temp_string;
getline(arg_is, temp_string);
arg_complex.set_value(temp_string);
return arg_is;
}
friend Complex operator+(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex(arg_complex1.Real::get_value() + arg_complex2.Real::get_value(),
arg_complex1.Imaginary::get_value() + arg_complex2.Imaginary::get_value());
return temp_complex;
}
friend Complex operator-(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex(arg_complex1.Real::get_value() - arg_complex2.Real::get_value(),
arg_complex1.Imaginary::get_value() - arg_complex2.Imaginary::get_value());
return temp_complex;
}
friend Complex operator*(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex(arg_complex1.Real::get_value() * arg_complex2.Real::get_value() -
arg_complex1.Imaginary::get_value() * arg_complex2.Imaginary::get_value(),
arg_complex1.Real::get_value() * arg_complex2.Imaginary::get_value() +
arg_complex1.Imaginary::get_value() * arg_complex2.Real::get_value());
return temp_complex;
}
friend Complex operator/(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex(arg_complex1 * arg_complex2.reciprocal());
return temp_complex;
}
};
// Number calculator class declaration
class Number_Calc
{
private:
// define current value
Number *m_curr_val_ptr;
// define input value
Number *m_input_val_ptr;
// define operation
// `+`, `-`, `*`, `/`, and `=`
char m_op;
// define value type
// `(R)eal`, `(I)nterger`, `(C)omplex`
char m_val_type;
// define input status, turns `op` for true and turns `value` for false
bool m_op_input;
// calculate result
void _calc_result()
{
switch (m_op)
{
case '+':
m_curr_val_ptr->add_assign(m_input_val_ptr->get_string());
break;
case '-':
m_curr_val_ptr->sub_assign(m_input_val_ptr->get_string());
break;
case '*':
m_curr_val_ptr->mul_assign(m_input_val_ptr->get_string());
break;
case '/':
m_curr_val_ptr->div_assign(m_input_val_ptr->get_string());
break;
case '=':
m_curr_val_ptr->set_value(m_input_val_ptr->get_string());
break;
default:
break;
}
}
// operation functions
// set activation op to add
void _add()
{
m_op = '+';
m_op_input = false;
}
// set activation op to subtract
void _sub()
{
m_op = '-';
m_op_input = false;
}
// set activation op to multiply
void _mul()
{
m_op = '*';
m_op_input = false;
}
// set activation op to divide
void _div()
{
m_op = '/';
m_op_input = false;
}
// set activation op to assign
void _assign()
{
m_op = '=';
m_op_input = false;
}
public:
// Constructor
Number_Calc(const char &arg_type = 'C')
: m_curr_val_ptr(NULL), m_input_val_ptr(NULL), m_op('='), m_op_input(false), m_val_type(arg_type)
{
switch (m_val_type)
{
case 'R':
m_curr_val_ptr = new Real();
m_input_val_ptr = new Real();
break;
case 'C':
m_curr_val_ptr = new Complex();
m_input_val_ptr = new Complex();
break;
case 'I':
m_curr_val_ptr = new Integer();
m_input_val_ptr = new Integer();
break;
default:
cout << "Error: Invalid value type" << endl;
break;
}
}
// Copy constructor
Number_Calc(const Number_Calc &arg_comp_calc)
: m_op(arg_comp_calc.m_op), m_op_input(arg_comp_calc.m_op_input), m_val_type(arg_comp_calc.m_val_type)
{
switch (m_val_type)
{
case 'R':
m_curr_val_ptr = new Real(*(Real *)arg_comp_calc.m_curr_val_ptr);
m_input_val_ptr = new Real(*(Real *)arg_comp_calc.m_input_val_ptr);
break;
case 'C':
m_curr_val_ptr = new Complex(*(Complex *)arg_comp_calc.m_curr_val_ptr);
m_input_val_ptr = new Complex(*(Complex *)arg_comp_calc.m_input_val_ptr);
break;
case 'I':
m_curr_val_ptr = new Integer(*(Integer *)arg_comp_calc.m_curr_val_ptr);
m_input_val_ptr = new Integer(*(Integer *)arg_comp_calc.m_input_val_ptr);
break;
default:
cout << "Error: Invalid value type" << endl;
break;
}
}
// Destructor
~Number_Calc()
{
delete m_curr_val_ptr;
delete m_input_val_ptr;
}
// cin `>>` operator for set input value or operation
friend istream &operator>>(istream &arg_is, Number_Calc &arg_comp_calc)
{
string temp_string;
getline(arg_is, temp_string);
if (temp_string == "+")
{
arg_comp_calc._add();
}
else if (temp_string == "-")
{
arg_comp_calc._sub();
}
else if (temp_string == "*")
{
arg_comp_calc._mul();
}
else if (temp_string == "/")
{
arg_comp_calc._div();
}
else if (temp_string == "=")
{
arg_comp_calc._assign();
}
else
{
arg_comp_calc.m_input_val_ptr->set_value(temp_string);
arg_comp_calc.m_op_input = true;
arg_comp_calc._calc_result();
}
return arg_is;
}
// cout `<<` operator for print calculator status
// note: be careful about the format of output
// cout `<<` operator for print calculator status
friend ostream &operator<<(ostream &arg_os, const Number_Calc &arg_comp_calc)
{
arg_os << arg_comp_calc.m_curr_val_ptr->get_string();
return arg_os;
}
};
int main()
{
// create an instance of the class for Integer
Number_Calc calc_i('I');
for (int i = 0; i < 3; i++)
{
cin >> calc_i;
cout << calc_i << endl;
}
// create an instance of the class for Real
Number_Calc calc_r('R');
for (int i = 0; i < 3; i++)
{
cin >> calc_r;
cout << calc_r << endl;
}
// create an instance of the class for Complex
Number_Calc calc_c('C');
for (int i = 0; i < 3; i++)
{
cin >> calc_c;
cout << calc_c << endl;
}
}
Example 2: Complex Number & Triangles
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
using namespace std;
class Triangle_Complex; // forward declaration
class Integer
{
protected:
int m_int_value;
public:
Integer(int arg_int_value = 0) : m_int_value(arg_int_value)
{
}
Integer(const Integer &arg_int) : m_int_value(arg_int.m_int_value)
{
}
operator int() const
{
return m_int_value;
}
Integer &operator=(const Integer &arg_int)
{
m_int_value = arg_int.m_int_value;
return *this;
}
void set_int_value(int arg_int_value)
{
m_int_value = arg_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Integer &arg_integer)
{
arg_os << arg_integer.m_int_value;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Integer &arg_integer)
{
arg_is >> arg_integer.m_int_value;
return arg_is;
}
friend Integer operator+(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value + arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator-(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value - arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator*(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value * arg_integer2.m_int_value);
return temp_integer;
}
friend Integer operator/(const Integer &arg_integer1, const Integer &arg_integer2)
{
Integer temp_integer(arg_integer1.m_int_value / arg_integer2.m_int_value);
return temp_integer;
}
};
// Real is a Integer
class Real : public Integer
{
protected:
double m_after_decimal;
public:
Real(double arg_value = 0.0) : Integer((int)arg_value),
m_after_decimal(arg_value - (int)arg_value)
{
}
Real(const Real &arg_real) : Integer(arg_real),
m_after_decimal(arg_real.m_after_decimal)
{
}
operator double() const
{
return m_after_decimal + (double)m_int_value;
}
Real &operator=(const Real &arg_real)
{
m_int_value = arg_real.m_int_value;
m_after_decimal = arg_real.m_after_decimal;
return *this;
}
void set_real_value(double arg_value)
{
m_int_value = (int)arg_value;
m_after_decimal = arg_value - m_int_value;
}
friend ostream &operator<<(ostream &arg_os, const Real &arg_real)
{
arg_os << (double)arg_real;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Real &arg_real)
{
double temp_double;
arg_is >> temp_double;
arg_real.set_real_value(temp_double);
return arg_is;
}
friend Real operator+(const Real &arg_real1, const Real &arg_real2)
{
// call the Integer operator+ to add the Integer part
Integer temp_integer((Integer)arg_real1 + (Integer)arg_real2);
Real temp_real(arg_real1.m_after_decimal + arg_real2.m_after_decimal);
temp_real.set_int_value((int)temp_integer + (int)temp_real);
return temp_real;
}
friend Real operator-(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 - (double)arg_real2);
return temp_real;
}
friend Real operator*(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 * (double)arg_real2);
return temp_real;
}
friend Real operator/(const Real &arg_real1, const Real &arg_real2)
{
Real temp_real((double)arg_real1 / (double)arg_real2);
return temp_real;
}
};
class Imaginary
{
protected:
double m_imaginary_value;
public:
Imaginary(double arg_imaginary_value = 0.0) : m_imaginary_value(arg_imaginary_value)
{
}
Imaginary(const Imaginary &arg_imaginary) : m_imaginary_value(arg_imaginary.m_imaginary_value)
{
}
Imaginary &operator=(const Imaginary &arg_imaginary)
{
m_imaginary_value = arg_imaginary.m_imaginary_value;
return *this;
}
double get_imaginary_value() const
{
return m_imaginary_value;
}
void set_imaginary_value(double arg_imaginary_value)
{
m_imaginary_value = arg_imaginary_value;
}
friend ostream &operator<<(ostream &arg_os, const Imaginary &arg_imaginary)
{
arg_os << arg_imaginary.m_imaginary_value << "i";
return arg_os;
}
friend Imaginary operator+(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value + arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
friend Imaginary operator-(const Imaginary &arg_imaginary1, const Imaginary &arg_imaginary2)
{
Imaginary temp_imaginary(arg_imaginary1.m_imaginary_value - arg_imaginary2.m_imaginary_value);
return temp_imaginary;
}
};
class Complex : public Real, public Imaginary
{
public:
Complex(double arg_real_value = 0.0,
double arg_imaginary_value = 0.0)
: Real(arg_real_value),
Imaginary(arg_imaginary_value)
{
}
Complex(const Complex &arg_complex)
: Real(arg_complex),
Imaginary(arg_complex)
{
}
Complex &operator=(const Complex &arg_complex)
{
Real::operator=(arg_complex);
Imaginary::operator=(arg_complex);
return *this;
}
Complex reciprocal() const
{
Complex temp_complex(*this);
double temp_real_value = temp_complex;
double temp_imaginary_value = temp_complex.get_imaginary_value();
double temp_denominator = temp_real_value * temp_real_value + temp_imaginary_value * temp_imaginary_value;
temp_complex.set_real_value(temp_real_value / temp_denominator);
temp_complex.set_imaginary_value(-temp_imaginary_value / temp_denominator);
return temp_complex;
}
double get_magnitude() const
{
Real temp_real(*this);
return sqrt((double)(temp_real * temp_real) + get_imaginary_value() * get_imaginary_value());
}
Complex get_argument() const
{
double magnitude = get_magnitude();
Complex temp_complex((double)(*this) / magnitude, get_imaginary_value() / magnitude);
return temp_complex;
}
friend ostream &operator<<(ostream &arg_os, const Complex &arg_complex)
{
arg_os << (Real)arg_complex << " + " << (Imaginary)arg_complex;
return arg_os;
}
friend istream &operator>>(istream &arg_is, Complex &arg_complex)
{
string temp_string;
getline(arg_is, temp_string, '+');
arg_complex.set_real_value(stod(temp_string));
getline(arg_is, temp_string, 'i');
arg_complex.set_imaginary_value(stod(temp_string));
return arg_is;
}
friend Complex operator+(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 + (double)arg_complex2,
arg_complex1.get_imaginary_value() + arg_complex2.get_imaginary_value());
return temp_complex;
}
friend Complex operator-(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 - (double)arg_complex2,
arg_complex1.get_imaginary_value() - arg_complex2.get_imaginary_value());
return temp_complex;
}
friend Complex operator*(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex((double)arg_complex1 * (double)arg_complex2 -
arg_complex1.get_imaginary_value() * arg_complex2.get_imaginary_value(),
(double)arg_complex1 * arg_complex2.get_imaginary_value() +
arg_complex1.get_imaginary_value() * (double)arg_complex2);
return temp_complex;
}
friend Complex operator/(const Complex &arg_complex1, const Complex &arg_complex2)
{
Complex temp_complex(arg_complex1 * arg_complex2.reciprocal());
return temp_complex;
}
friend bool operator==(const Complex &arg_complex1, const Complex &arg_complex2)
{
return ((double)arg_complex1 == (double)arg_complex2) &&
(arg_complex1.get_imaginary_value() == arg_complex2.get_imaginary_value());
}
friend bool operator!=(const Complex &arg_complex1, const Complex &arg_complex2)
{
return !(arg_complex1 == arg_complex2);
}
friend bool operator<(const Complex &arg_complex1, const Complex &arg_complex2)
{
return ((double)arg_complex1 < (double)arg_complex2) ||
((double)arg_complex1 == (double)arg_complex2 &&
arg_complex1.get_imaginary_value() < arg_complex2.get_imaginary_value());
}
friend bool operator>(const Complex &arg_complex1, const Complex &arg_complex2)
{
return arg_complex2 < arg_complex1;
}
friend bool operator<=(const Complex &arg_complex1, const Complex &arg_complex2)
{
return !(arg_complex1 > arg_complex2);
}
friend bool operator>=(const Complex &arg_complex1, const Complex &arg_complex2)
{
return !(arg_complex1 < arg_complex2);
}
friend class Triangle_Complex;
};
// Triangle_Complex class declaration
class Triangle_Complex
{
protected:
// define three points of the Triangle_Complex
// Triangle 'has-a' Complex, so it use composition
Complex m_point[3];
// check & correct the Triangle_Complex points to counterclockwise order
void _check_points()
{
// if the area is negative, swap the points
if (area() < 0.0)
{
Complex temp = m_point[0];
m_point[0] = m_point[1];
m_point[1] = temp;
}
}
public:
// Constructor
Triangle_Complex(const Complex &arg_point1,
const Complex &arg_point2,
const Complex &arg_point3)
: m_point{arg_point1, arg_point2, arg_point3}
{
_check_points();
}
// Copy constructor
Triangle_Complex(const Triangle_Complex &arg_triangle)
: m_point{arg_triangle.m_point[0], arg_triangle.m_point[1], arg_triangle.m_point[2]}
{
}
// Destructor
~Triangle_Complex() {} // do nothing
// modify the three points of the Triangle_Complex
virtual void set_points(const Complex &arg_point1,
const Complex &arg_point2,
const Complex &arg_point3)
{
m_point[0] = arg_point1;
m_point[1] = arg_point2;
m_point[2] = arg_point3;
_check_points();
}
virtual void set_point1(const Complex &arg_point1)
{
m_point[0] = arg_point1;
_check_points();
}
virtual void set_point2(const Complex &arg_point2)
{
m_point[1] = arg_point2;
_check_points();
}
virtual void set_point3(const Complex &arg_point3)
{
m_point[2] = arg_point3;
_check_points();
}
// get the three points of the Triangle_Complex
Complex get_point1() const
{
return m_point[0];
}
Complex get_point2() const
{
return m_point[1];
}
Complex get_point3() const
{
return m_point[2];
}
// calculate the area of the Triangle_Complex
double area()
{
double area = 0.0;
for (int i = 0; i < 3; i++)
{
area += (double)m_point[i] * m_point[(i + 1) % 3].get_imaginary_value();
area -= m_point[i].get_imaginary_value() * (double)m_point[(i + 1) % 3];
}
return area / 2.0;
}
// print the Triangle_Complex
// format: (c1, c2, c3)
friend std::ostream &operator<<(std::ostream &arg_os, const Triangle_Complex &arg_tri)
{
arg_os << "(";
for (int i = 0; i < 3; i++)
{
arg_os << arg_tri.m_point[i];
if (i < 2)
arg_os << ", ";
}
arg_os << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: (c1, c2, c3) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Triangle_Complex &arg_tri)
{
string temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
for (int i = 0; i < 3; i++)
{
arg_is >> arg_tri.m_point[i];
if (i < 2)
{
getline(arg_is, temp, ','); // ignore the ','
}
}
getline(arg_is, temp, ')'); // ignore the last ')'
}
// check & correct the Triangle_Complex points to counterclockwise order
arg_tri._check_points();
return arg_is;
}
};
class Equilateral_Triangle_Complex : public Triangle_Complex
// Equilateral Triangle `is-a' Triangle_Complex, so it use inheritance
// use function overloading to implement the different function
// of Equilateral_Triangle_Complex
// details will be discussed in polymorphism (next chapter)
{
public:
Equilateral_Triangle_Complex(const Complex &arg_point1,
const Complex &arg_point2)
: Triangle_Complex(arg_point1, arg_point2, arg_point1)
{
Complex temp = arg_point2 - arg_point1;
temp = temp * Complex(0.5, sqrt(3.0) / 2.0); // rotate 60 degree
m_point[2] = arg_point1 + temp; // calculate the third point
_check_points();
}
void set_points(const Complex &arg_point1,
const Complex &arg_point2,
const Complex &arg_point3)
{
m_point[0] = arg_point1;
m_point[1] = arg_point2;
Complex temp = arg_point2 - arg_point1;
temp = temp * Complex(0.5, sqrt(3.0) / 2.0); // rotate 60 degree
m_point[2] = arg_point1 + temp; // calculate the third point
_check_points();
}
void set_point1(const Complex &arg_point1)
{
// invalid operation
}
void set_point2(const Complex &arg_point2)
{
// invalid operation
}
void set_point3(const Complex &arg_point3)
{
// invalid operation
}
// read the coordinate of a point from the input,
// format: (c1, c2, c3) and ignore c3 and spaces
friend std::istream &operator>>(std::istream &arg_is,
Equilateral_Triangle_Complex &arg_tri)
{
string temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
for (int i = 0; i < 3; i++)
{
if (i < 2)
{
arg_is >> arg_tri.m_point[i];
getline(arg_is, temp, ','); // ignore the ','
}
}
getline(arg_is, temp, ')'); // ignore the c3 and last ')'
}
// check & correct the Triangle_Complex points to counterclockwise order
arg_tri._check_points();
return arg_is;
}
};
// main function
int main()
{
// create a Equilateral_Triangle_Complex
Triangle_Complex *t = new Equilateral_Triangle_Complex(Complex(1, 1), Complex(2, 2));
cout << *t << endl;
cout << "Area: " << t->area() << endl;
// change the points of the Equilateral_Triangle_Complex
t->set_points(Complex(3, 3), Complex(2, 2), Complex(3, 0));
cout << *t << endl;
cout << "Area: " << t->area() << endl;
delete t;
// change the object to Triangle_Complex
t = new Triangle_Complex(Complex(1, 1), Complex(2, 2), Complex(3, 0));
cout << *t << endl;
cout << "Area: " << t->area() << endl;
// change the points of the Triangle_Complex
t->set_points(Complex(3, 3), Complex(2, 2), Complex(3, 0));
cout << *t << endl;
cout << "Area: " << t->area() << endl;
delete t;
return 0;
}
Lab 12: Complex Number's Geometry & Operations
Lab 12-1: Complex Number's Geometry (40%)
- 輸入:
- 以
char格式輸入幾何圖形形狀,包含三角形 (t)、四邊形 (q)、多邊形 (p)、圓形c,一行輸入一個幾何圖形 - 以
unsigned int格式輸入幾何圖形的頂點數,一行輸入一個正整數- 三角形:3
- 四邊形:4
- 多邊形:大於 3 的正整數
- 圓形:2
- 以
double格式輸入組合幾何圖形的複數的實數及虛數部分,以空格分開,一行輸入一個複數 - 輸入幾何圖形形狀及頂點數後依據 2. 的頂點數接著輸入相對應的複數
- 三角形:連續輸入三個複數
- 四邊形:連續輸入四個複數
- 多邊形:連續輸入多個複數
- 圓形:連續輸入兩個複數
- 輸入 Ctrl+D 結束程式
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
^Z) 再輸入 Enter (Format 中的⏎) 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
- 以
- 輸出:
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 格式請參考 Format 中的說明
- 頂點順序與輸入順序相同
- 複數的格式為
(-)<real result> (+|-) (<imag result>i)- 若虛數部分為 0 則僅顯示實數部分
- 若虛數部分小於 0 則中間的
+要改成-,並且虛數部分要顯示絕對值
- 虛數及實數部分皆以預設
double格式顯示
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 檔名:
lab12-1_<學號>.cpp(e.g.lab12-1_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果
- 使用者不需要處理錯誤輸入
- 請使用 pseudo code 提供的
mainfunction 來處理輸入與輸出 - 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Format
<geometry type>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<geometry type>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
^Z⏎
Example
Triangle
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
^Z⏎
Quadrilateral
$ ./a.out
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
^Z⏎
Circle
$ ./a.out
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
^Z⏎
Polygon
$ ./a.out
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
^Z⏎
Multiple Objects
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
^Z⏎
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry();
// parse the cin to the geometry
virtual void parse_geometry(istream &arg_is);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
// used for process the test cases, do not modify
int main()
{
string input;
Geometry_Comp *geo_ptr = 0;
while (getline(cin, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
}
// parse the cin to the geometry
geo_ptr->parse_geometry(cin);
// print the geometry
geo_ptr->print_geometry();
// delete the pointer
delete geo_ptr;
}
return 0;
}
Reference Code:
TA
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry();
// parse the cin to the geometry
virtual void parse_geometry(istream &arg_is);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
// Complex class implementation
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
// Copy constructor
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
// assignment operator
Complex &Complex::operator=(const Complex &arg_c)
{
if (this == &arg_c) // self-assignment
return *this;
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
// cout `<<` operator for print complex number
// note: be careful about the format of output
ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag > 0)
{
arg_os << arg_c.m_real << " + " << arg_c.m_imag << "i";
}
else if (arg_c.m_imag < 0)
{
arg_os << arg_c.m_real << " - " << -arg_c.m_imag << "i";
}
else
{
arg_os << arg_c.m_real;
}
return arg_os;
}
// cin `>>` operator for input complex number
// note: be careful about the format of input
istream &operator>>(istream &arg_is, Complex &arg_c)
{
double input_real, input_imag;
arg_is >> input_real;
if (arg_is.fail())
{
error_and_exit();
}
arg_is >> input_imag;
if (arg_is.fail() || !arg_is.eof())
{
error_and_exit();
}
arg_c.m_real = input_real;
arg_c.m_imag = input_imag;
return arg_is;
}
// Geometry_Comp class implementation
// Constructor, initializes the array
Geometry_Comp::Geometry_Comp(const unsigned int &arg_num_of_vertex)
: m_comp_array(arg_num_of_vertex)
{
}
// Copy constructor
Geometry_Comp::Geometry_Comp(const Geometry_Comp &arg_gc)
: m_comp_array(arg_gc.m_comp_array)
{
}
// assignment operator
Geometry_Comp &Geometry_Comp::operator=(const Geometry_Comp &arg_gc)
{
if (this == &arg_gc) // self-assignment
return *this;
m_comp_array = arg_gc.m_comp_array;
return *this;
}
// print the geometry
void Geometry_Comp::print_geometry()
{
cout << "not implemented" << endl;
}
// parse the cin to the geometry
void Geometry_Comp::parse_geometry(istream &arg_is)
{
cout << "not implemented" << endl;
}
// set the geometry
void Geometry_Comp::set_geometry(const vector<Complex> &arg_comp_array)
{
m_comp_array = arg_comp_array;
}
// get the geometry array
vector<Complex> Geometry_Comp::get_geometry_array()
{
return m_comp_array;
}
// Triangle_Comp class implementation
// Constructor, initializes the array
Triangle_Comp::Triangle_Comp()
: Geometry_Comp(triangle_num_of_vertex)
{
}
// Copy constructor
Triangle_Comp::Triangle_Comp(const Triangle_Comp &arg_tc)
: Geometry_Comp(arg_tc)
{
}
// assignment operator
Triangle_Comp &Triangle_Comp::operator=(const Triangle_Comp &arg_tc)
{
if (this == &arg_tc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_tc);
return *this;
}
// print the geometry
void Triangle_Comp::print_geometry()
{
cout << "t" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < triangle_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Triangle_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != triangle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Quadrilateral_Comp class implementation
// Constructor, initializes the array
Quadrilateral_Comp::Quadrilateral_Comp()
: Geometry_Comp(quadrilateral_num_of_vertex)
{
}
// Copy constructor
Quadrilateral_Comp::Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc)
: Geometry_Comp(arg_qc)
{
}
// assignment operator
Quadrilateral_Comp &Quadrilateral_Comp::operator=(const Quadrilateral_Comp &arg_qc)
{
if (this == &arg_qc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_qc);
return *this;
}
// print the geometry
void Quadrilateral_Comp::print_geometry()
{
cout << "q" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < quadrilateral_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Quadrilateral_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != quadrilateral_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Polygon_Comp class implementation
// Constructor, initializes the array
Polygon_Comp::Polygon_Comp()
: Geometry_Comp()
{
}
// Copy constructor
Polygon_Comp::Polygon_Comp(const Polygon_Comp &arg_pc)
: Geometry_Comp(arg_pc)
{
}
// assignment operator
Polygon_Comp &Polygon_Comp::operator=(const Polygon_Comp &arg_pc)
{
if (this == &arg_pc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_pc);
return *this;
}
// print the geometry
void Polygon_Comp::print_geometry()
{
cout << "p" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < m_comp_array.size(); i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Polygon_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num < triangle_num_of_vertex)
{
error_and_exit();
}
m_comp_array.resize(vertex_num);
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Circle_Comp class implementation
// Constructor, initializes the array
Circle_Comp::Circle_Comp()
: Geometry_Comp(circle_num_of_vertex)
{
}
// Copy constructor
Circle_Comp::Circle_Comp(const Circle_Comp &arg_cc)
: Geometry_Comp(arg_cc)
{
}
// assignment operator
Circle_Comp &Circle_Comp::operator=(const Circle_Comp &arg_cc)
{
if (this == &arg_cc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_cc);
return *this;
}
// print the geometry
void Circle_Comp::print_geometry()
{
cout << "c" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < circle_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Circle_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != circle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// used for process the test cases, do not modify
int main()
{
string input;
Geometry_Comp *geo_ptr = 0;
while (getline(cin, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
default:
error_and_exit();
}
// parse the cin to the geometry
geo_ptr->parse_geometry(cin);
// print the geometry
geo_ptr->print_geometry();
// delete the pointer
delete geo_ptr;
}
return 0;
}
Lab 12-2: Simple Complex Number Geometry Transformation (40%)
- 輸入:
- 幾何圖形
- 以
char格式輸入幾何圖形形狀,包含三角形 (t)、四邊形 (q)、多邊形 (p)、圓形 (c),一行輸入一個幾何圖形 - 以
unsigned int格式輸入幾何圖形的頂點數,一行輸入一個正整數- 三角形:3
- 四邊形:4
- 多邊形:大於 3 的正整數
- 圓形:2
- 以
double格式輸入組合幾何圖形的複數的實數及虛數部分,以空格分開,一行輸入一個複數 - 輸入幾何圖形形狀及頂點數後依據 2. 的頂點數接著輸入相對應的複數
- 三角形:連續輸入三個複數
- 四邊形:連續輸入四個複數
- 多邊形:連續輸入多個複數
- 圓形:連續輸入兩個複數
- 幾何變換
- 以
char格式輸入幾何變換字元,包含以0點旋轉 (r)、以0點縮放 (z)、平移 (m),一行輸入一個幾何變換 - 以
double格式輸入幾何變換的複數的實數及虛數部分,以空格分開,一行輸入一個複數- 以
0點旋轉:\(z * (cos(\theta) + sin(\theta)i), norm = 1\) - 以
0點縮放:\(z * (r + 0i)\) - 平移:\(z + (x + yi)\)
- 以
- 輸入幾何變換後須將所有的幾何圖形複數變換
- 輸入 Ctrl+D 結束程式
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
^Z) 再輸入 Enter (Format 中的⏎) 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
- 輸出:
- 幾何圖形
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 格式請參考 Format 中的說明
- 頂點順序與輸入順序相同
- 複數的格式為
(-)<real result> (+|-) (<imag result>i)- 若虛數部分為 0 則僅顯示實數部分
- 若虛數部分小於 0 則中間的
+要改成-,並且虛數部分要顯示絕對值
- 虛數及實數部分皆以預設
double格式顯示
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 幾何變換
- 輸出變換後的所有幾何圖形複數
- 幾何圖形
- 檔名:
lab12-2_<學號>.cpp(e.g.lab12-2_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果
- 使用者不需要處理錯誤輸入
- 請使用 pseudo code 提供的
main來處理輸入與輸出 - 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Format
Input
<geometry type>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<geometry type>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
Transformation
<geometry type 1>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<geometry type 1>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
<geometry type 2>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<geometry type 2>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
<geometry transformation type>⏎
(-)<real trans> (+|-) (<imag trans>i)⏎
<geometry type 1>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
<geometry type 2>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
...
^Z⏎
Example
Input
Triangle
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
^Z⏎
Quadrilateral
$ ./a.out
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
^Z⏎
Circle
$ ./a.out
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
^Z⏎
Polygon
$ ./a.out
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
^Z⏎
Multiple Objects
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
^Z⏎
Transformation
Scaling
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
z⏎
2.0 0.0⏎
t
3
2 + 4i
6 + 8i
10
^Z⏎
Translation
$ ./a.out
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
m⏎
3.0 -1.0⏎
q
4
4 + 1i
6 + 1i
6 + 3i
4 + 3i
^Z⏎
Rotation
$ ./a.out
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
r⏎
0.99990604980155 0.013707354604752⏎
c
2
0.972491 + 2.01352i
2.94489 + 4.04075i
^Z⏎
Multiple Transformations
$ ./a.out
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
z⏎
2.0 0.0⏎
p
5
2
4 + 2.2i
-6 - 4.4i
8.6 + 4.2i
-2.4 + 6.8i
m⏎
3.0 -1.0⏎
p
5
5 - 1i
7 + 1.2i
-3 - 5.4i
11.6 + 3.2i
0.6 + 5.8i
r⏎
0.99990604980155 0.013707354604752⏎
p
5
5.01324 - 0.931369i
6.98289 + 1.29584i
-2.9257 - 5.44061i
11.555 + 3.3587i
0.520441 + 5.80768i
^Z⏎
Multiple Transformations on Multiple Objects
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
z⏎
2.0 0.0⏎
t
3
2 + 4i
6 + 8i
10
q
4
2 + 4i
6 + 4i
6 + 8i
2 + 8i
c
2
2 + 4i
6 + 8i
p
5
2
4 + 2.2i
-6 - 4.4i
8.6 + 4.2i
-2.4 + 6.8i
m⏎
3.0 -1.0⏎
t
3
5 + 3i
9 + 7i
13 - 1i
q
4
5 + 3i
9 + 3i
9 + 7i
5 + 7i
c
2
5 + 3i
9 + 7i
p
5
5 - 1i
7 + 1.2i
-3 - 5.4i
11.6 + 3.2i
0.6 + 5.8i
r⏎
0.99990604980155 0.013707354604752⏎
t
3
4.95841 + 3.06825i
8.9032 + 7.12271i
13.0125 - 0.82171i
q
4
4.95841 + 3.06825i
8.95803 + 3.12308i
8.9032 + 7.12271i
4.90358 + 7.06788i
c
2
4.95841 + 3.06825i
8.9032 + 7.12271i
p
5
5.01324 - 0.931369i
6.98289 + 1.29584i
-2.9257 - 5.44061i
11.555 + 3.3587i
0.520441 + 5.80768i
^Z⏎
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// length of the complex number
double length() const;
// angle of the complex number in radians
// use `atan2` to compute the angle by the formula `atan(imag/real)`
// and use `NAN` for 0/0 case
// `atan2` ref: https://en.cppreference.com/w/cpp/numeric/math/atan2
// `NAN` ref: https://en.cppreference.com/w/cpp/numeric/math/NAN
double angle() const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
// utility function to check if the transformation is valid
// hint: use `isnan` to check the angle is valid or not
// ref: https://en.cppreference.com/w/cpp/numeric/math/isnan
bool _check_transform(const Complex &arg_trans_c, const char &arg_op);
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry();
// parse the cin to the geometry
virtual void parse_geometry(istream &arg_is);
// apply transformation to the geometry
void transform_geometry(const Complex &arg_trans_c, const char &arg_op);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
// used for process the test cases, do not modify
int main()
{
string input, temp;
vector<Geometry_Comp *> geo_ptr_array;
Geometry_Comp *geo_ptr;
Complex trans_c;
char trans_op;
while (getline(cin, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
case 'r':
case 'z':
case 'm':
getline(cin, temp);
break;
}
if (input[0] == 't' || input[0] == 'q' || input[0] == 'p' || input[0] == 'c')
{
// parse the cin to the geometry
geo_ptr->parse_geometry(cin);
// print the geometry
geo_ptr->print_geometry();
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else if (input[0] == 'r' || input[0] == 'z' || input[0] == 'm')
{
stringstream ss(temp);
ss >> trans_c;
// transform the geometry using operator and complex
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->transform_geometry(trans_c, input[0]);
// print transformed geometry
geo_ptr_array[i]->print_geometry();
}
}
}
return 0;
}
Reference Code:
TA
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// length of the complex number
double length() const;
// angle of the complex number in radians
double angle() const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
// utility function to check if the transformation is valid
bool _check_transform(const Complex &arg_trans_c, const char &arg_op);
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry();
// parse the cin to the geometry
virtual void parse_geometry(istream &arg_is);
// apply transformation to the geometry
void transform_geometry(const Complex &arg_trans_c, const char &arg_op);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
// Complex class implementation
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
// Copy constructor
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
// assignment operator
Complex &Complex::operator=(const Complex &arg_c)
{
if (this == &arg_c) // self-assignment
return *this;
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
// add assignment operator
Complex &Complex::operator+=(const Complex &arg_c)
{
m_real += arg_c.m_real;
m_imag += arg_c.m_imag;
return *this;
}
// multiply assignment operator
Complex &Complex::operator*=(const Complex &arg_c)
{
double real = m_real * arg_c.m_real - m_imag * arg_c.m_imag;
double imag = m_real * arg_c.m_imag + m_imag * arg_c.m_real;
m_real = real;
m_imag = imag;
return *this;
}
// length of the complex number
double Complex::length() const
{
return sqrt(m_real * m_real + m_imag * m_imag);
}
// angle of the complex number in radians
double Complex::angle() const
{
if (m_real == 0 && m_imag == 0)
{
return NAN;
}
return atan2(m_imag, m_real);
}
// cout `<<` operator for print complex number
// note: be careful about the format of output
ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag > 0)
{
arg_os << arg_c.m_real << " + " << arg_c.m_imag << "i";
}
else if (arg_c.m_imag < 0)
{
arg_os << arg_c.m_real << " - " << -arg_c.m_imag << "i";
}
else
{
arg_os << arg_c.m_real;
}
return arg_os;
}
// cin `>>` operator for input complex number
// note: be careful about the format of input
istream &operator>>(istream &arg_is, Complex &arg_c)
{
double input_real, input_imag;
arg_is >> input_real;
if (arg_is.fail())
{
error_and_exit();
}
arg_is >> input_imag;
if (arg_is.fail() || !arg_is.eof())
{
error_and_exit();
}
arg_c.m_real = input_real;
arg_c.m_imag = input_imag;
return arg_is;
}
// Geometry_Comp class implementation
// check if the transformation is valid
bool Geometry_Comp::_check_transform(const Complex &arg_c, const char &arg_op)
{
// check if the operation is valid
if (arg_op == 'r' && (arg_c.length() != 1 || isnan(arg_c.angle())))
{
return false;
}
else if (arg_op == 'z' && (arg_c.m_real == 0 || arg_c.m_imag != 0))
{
return false;
}
else
{
return true;
}
}
// Constructor, initializes the array
Geometry_Comp::Geometry_Comp(const unsigned int &arg_num_of_vertex)
: m_comp_array(arg_num_of_vertex)
{
}
// Copy constructor
Geometry_Comp::Geometry_Comp(const Geometry_Comp &arg_gc)
: m_comp_array(arg_gc.m_comp_array)
{
}
// assignment operator
Geometry_Comp &Geometry_Comp::operator=(const Geometry_Comp &arg_gc)
{
if (this == &arg_gc) // self-assignment
return *this;
m_comp_array = arg_gc.m_comp_array;
return *this;
}
// print the geometry
void Geometry_Comp::print_geometry()
{
cout << "not implemented" << endl;
}
// parse the cin to the geometry
void Geometry_Comp::parse_geometry(istream &arg_is)
{
cout << "not implemented" << endl;
}
// apply transformation to the geometry
void Geometry_Comp::transform_geometry(const Complex &arg_c, const char &arg_op)
{
if (!(_check_transform(arg_c, arg_op)))
{
error_and_exit();
}
if (arg_op == 'm')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] += arg_c;
}
}
else if (arg_op == 'r' || arg_op == 'z')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] *= arg_c;
}
}
}
// set the geometry
void Geometry_Comp::set_geometry(const vector<Complex> &arg_comp_array)
{
m_comp_array = arg_comp_array;
}
// get the geometry array
vector<Complex> Geometry_Comp::get_geometry_array()
{
return m_comp_array;
}
// Triangle_Comp class implementation
// Constructor, initializes the array
Triangle_Comp::Triangle_Comp()
: Geometry_Comp(triangle_num_of_vertex)
{
}
// Copy constructor
Triangle_Comp::Triangle_Comp(const Triangle_Comp &arg_tc)
: Geometry_Comp(arg_tc)
{
}
// assignment operator
Triangle_Comp &Triangle_Comp::operator=(const Triangle_Comp &arg_tc)
{
if (this == &arg_tc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_tc);
return *this;
}
// print the geometry
void Triangle_Comp::print_geometry()
{
cout << "t" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < triangle_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Triangle_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
stringstream ss(temp);
unsigned int vertex_num;
ss >> vertex_num;
if (vertex_num != triangle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Quadrilateral_Comp class implementation
// Constructor, initializes the array
Quadrilateral_Comp::Quadrilateral_Comp()
: Geometry_Comp(quadrilateral_num_of_vertex)
{
}
// Copy constructor
Quadrilateral_Comp::Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc)
: Geometry_Comp(arg_qc)
{
}
// assignment operator
Quadrilateral_Comp &Quadrilateral_Comp::operator=(const Quadrilateral_Comp &arg_qc)
{
if (this == &arg_qc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_qc);
return *this;
}
// print the geometry
void Quadrilateral_Comp::print_geometry()
{
cout << "q" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < quadrilateral_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Quadrilateral_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != quadrilateral_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Polygon_Comp class implementation
// Constructor, initializes the array
Polygon_Comp::Polygon_Comp()
: Geometry_Comp()
{
}
// Copy constructor
Polygon_Comp::Polygon_Comp(const Polygon_Comp &arg_pc)
: Geometry_Comp(arg_pc)
{
}
// assignment operator
Polygon_Comp &Polygon_Comp::operator=(const Polygon_Comp &arg_pc)
{
if (this == &arg_pc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_pc);
return *this;
}
// print the geometry
void Polygon_Comp::print_geometry()
{
cout << "p" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < m_comp_array.size(); i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Polygon_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num < triangle_num_of_vertex)
{
error_and_exit();
}
m_comp_array.resize(vertex_num);
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Circle_Comp class implementation
// Constructor, initializes the array
Circle_Comp::Circle_Comp()
: Geometry_Comp(circle_num_of_vertex)
{
}
// Copy constructor
Circle_Comp::Circle_Comp(const Circle_Comp &arg_cc)
: Geometry_Comp(arg_cc)
{
}
// assignment operator
Circle_Comp &Circle_Comp::operator=(const Circle_Comp &arg_cc)
{
if (this == &arg_cc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_cc);
return *this;
}
// print the geometry
void Circle_Comp::print_geometry()
{
cout << "c" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < circle_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Circle_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != circle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
int main()
{
string input, temp;
vector<Geometry_Comp *> geo_ptr_array;
Geometry_Comp *geo_ptr;
Complex trans_c;
char trans_op;
while (getline(cin, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
case 'r':
case 'z':
case 'm':
getline(cin, temp);
break;
default:
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
if (input[0] == 't' || input[0] == 'q' || input[0] == 'p' || input[0] == 'c')
{
// parse the cin to the geometry
geo_ptr->parse_geometry(cin);
// print the geometry
geo_ptr->print_geometry();
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else if (input[0] == 'r' || input[0] == 'z' || input[0] == 'm')
{
stringstream ss(temp);
ss >> trans_c;
// transform the geometry using operator and complex
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->transform_geometry(trans_c, input[0]);
// print transformed geometry
geo_ptr_array[i]->print_geometry();
}
}
else
{
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
}
return 0;
}
Lab 12-3: Enhanced Complex Number Geometry Transformation (20%)
- 輸入:
- 幾何圖形
- 以
char格式輸入幾何圖形形狀,包含三角形 (t)、四邊形 (q)、多邊形 (p)、圓形 (c),一行輸入一個幾何圖形 - 以
unsiged int格式輸入幾何圖形的頂點數,一行輸入一個正整數- 三角形:3
- 四邊形:4
- 多邊形:大於 3 的正整數
- 圓形:2
- 以
double格式輸入組合幾何圖形的複數的實數及虛數部分,以空格分開,一行輸入一個複數 - 輸入幾何圖形形狀及頂點數後依據 2. 的頂點數接著輸入相對應的複數
- 三角形:連續輸入三個複數
- 四邊形:連續輸入四個複數
- 多邊形:連續輸入多個複數
- 圓形:連續輸入兩個複數
- 幾何變換
- 以
char格式輸入幾何變換字元,包含以0點旋轉 (r)、以0點縮放 (z)、平移 (m),一行輸入一個幾何變換 - 以
double格式輸入幾何變換的複數的實數及虛數部分,以空格分開,一行輸入一個複數- 以
0點旋轉:\(z * (cos(\theta) + sin(\theta)i), norm = 1\) - 以
0點縮放:\(z * (r + 0i)\) - 平移:\(z + (x + yi)\)
- 以
- 輸入幾何變換後須將所有的幾何圖形複數變換
- 輸入 Ctrl+D 結束程式
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
^Z) 再輸入 Enter (Format 中的⏎) 完成輸入
- Windows 請輸入 Ctrl+Z (會在螢幕上顯示
- 程式輸入以行為單位,每行輸入為任何有效的
string格式
- 輸出:
- 幾何圖形
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 格式請參考 Format 中的說明
- 頂點順序與輸入順序相同
- 複數的格式為
(-)<real result> (+|-) (<imag result>i)- 若虛數部分為 0 則僅顯示實數部分
- 若虛數部分小於 0 則中間的
+要改成-,並且虛數部分要顯示絕對值
- 虛數及實數部分皆以預設
double格式顯示
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 幾何變換
- 輸出變換後的所有幾何圖形複數
- 若使用者輸入的複數、幾何圖形或幾何變換不正確,則顯示錯誤訊息
Error: Invalid input並結束程式
- 幾何圖形
- 檔名:
lab12-3_<學號>.cpp(e.g.lab12-3_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果或錯誤訊息
- 程式僅需處裡輸入格式錯誤的例外狀況,如輸入的複數、幾何圖形或幾何變換不正確,其餘錯誤不須處裡
- 請基於 pseudo code 提供的
main進行修改來處理輸入與輸出 - 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Format
Input
<geometry type>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<geometry type>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
Transformation
<geometry type 1>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<geometry type 1>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
<geometry type 2>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<geometry type 2>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
<geometry transformation type>⏎
(-)<real trans> (+|-) (<imag trans>i)⏎
<geometry type 1>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
<geometry type 2>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
...
^Z⏎
Example
Input
Triangle
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
^Z⏎
Quadrilateral
$ ./a.out
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
^Z⏎
Circle
$ ./a.out
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
^Z⏎
Polygon
$ ./a.out
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
^Z⏎
Multiple Objects
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
^Z⏎
Transformation
Scaling
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
z⏎
2.0 0.0⏎
t
3
2 + 4i
6 + 8i
10
^Z⏎
Translation
$ ./a.out
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
m⏎
3.0 -1.0⏎
q
4
4 + 1i
6 + 1i
6 + 3i
4 + 3i
^Z⏎
Rotation
$ ./a.out
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
r⏎
0.99990604980155 0.013707354604752⏎
c
2
0.972491 + 2.01352i
2.94489 + 4.04075i
^Z⏎
Multiple Transformations
$ ./a.out
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
z⏎
2.0 0.0⏎
p
5
2
4 + 2.2i
-6 - 4.4i
8.6 + 4.2i
-2.4 + 6.8i
m⏎
3.0 -1.0⏎
p
5
5 - 1i
7 + 1.2i
-3 - 5.4i
11.6 + 3.2i
0.6 + 5.8i
r⏎
0.99990604980155 0.013707354604752⏎
p
5
5.01324 - 0.931369i
6.98289 + 1.29584i
-2.9257 - 5.44061i
11.555 + 3.3587i
0.520441 + 5.80768i
^Z⏎
Multiple Transformations on Multiple Objects
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
z⏎
2.0 0.0⏎
t
3
2 + 4i
6 + 8i
10
q
4
2 + 4i
6 + 4i
6 + 8i
2 + 8i
c
2
2 + 4i
6 + 8i
p
5
2
4 + 2.2i
-6 - 4.4i
8.6 + 4.2i
-2.4 + 6.8i
m⏎
3.0 -1.0⏎
t
3
5 + 3i
9 + 7i
13 - 1i
q
4
5 + 3i
9 + 3i
9 + 7i
5 + 7i
c
2
5 + 3i
9 + 7i
p
5
5 - 1i
7 + 1.2i
-3 - 5.4i
11.6 + 3.2i
0.6 + 5.8i
r⏎
0.99990604980155 0.013707354604752⏎
t
3
4.95841 + 3.06825i
8.9032 + 7.12271i
13.0125 - 0.82171i
q
4
4.95841 + 3.06825i
8.95803 + 3.12308i
8.9032 + 7.12271i
4.90358 + 7.06788i
c
2
4.95841 + 3.06825i
8.9032 + 7.12271i
p
5
5.01324 - 0.931369i
6.98289 + 1.29584i
-2.9257 - 5.44061i
11.555 + 3.3587i
0.520441 + 5.80768i
^Z⏎
Exception Handling
Wrong object type or transformation type
$ ./a.out
a⏎
Error: Invalid input
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
l⏎
Error: Invalid input
Wrong object or veterx format
$ ./a.out
t⏎
1234adsfdf⏎
Error: Invalid input
$ ./a.out
t⏎
5⏎
Error: Invalid input
$ ./a.out
$ ./a.out
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
3.0 2.0⏎
Error: Invalid input
Wrong complex number format
$ ./a.out
t⏎
3⏎
asdfjsoidfjpsdiofj⏎
Error: Invalid input
$ ./a.out
t⏎
3⏎
1.0 asdfjsoidfjpsdiofj⏎
Error: Invalid input
$ ./a.out
t⏎
3⏎
1.0⏎
Error: Invalid input
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// length of the complex number
double length() const;
// angle of the complex number in radians
// use `atan2` to compute the angle by the formula `atan(imag/real)`
// and use `NAN` for 0/0 case
// `atan2` ref: https://en.cppreference.com/w/cpp/numeric/math/atan2
// `NAN` ref: https://en.cppreference.com/w/cpp/numeric/math/NAN
double angle() const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
// utility function to check if the transformation is valid
// hint: use `isnan` to check the angle is valid or not
// ref: https://en.cppreference.com/w/cpp/numeric/math/isnan
bool _check_transform(const Complex &arg_trans_c, const char &arg_op);
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry();
// parse the cin to the geometry
virtual void parse_geometry(istream &arg_is);
// apply transformation to the geometry
void transform_geometry(const Complex &arg_trans_c, const char &arg_op);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
int main()
{
string input, temp;
vector<Geometry_Comp *> geo_ptr_array;
Geometry_Comp *geo_ptr;
Complex trans_c;
char trans_op;
while (getline(cin, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
case 'r':
case 'z':
case 'm':
getline(cin, temp);
break;
}
if (input[0] == 't' || input[0] == 'q' || input[0] == 'p' || input[0] == 'c')
{
// parse the cin to the geometry
geo_ptr->parse_geometry(cin);
// print the geometry
geo_ptr->print_geometry();
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else if (input[0] == 'r' || input[0] == 'z' || input[0] == 'm')
{
stringstream ss(temp);
ss >> trans_c;
// transform the geometry using operator and complex
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->transform_geometry(trans_c, input[0]);
// print transformed geometry
geo_ptr_array[i]->print_geometry();
}
}
}
return 0;
}
Reference Code:
TA
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// length of the complex number
double length() const;
// angle of the complex number in radians
double angle() const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
// utility function to check if the transformation is valid
bool _check_transform(const Complex &arg_trans_c, const char &arg_op);
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry();
// parse the cin to the geometry
virtual void parse_geometry(istream &arg_is);
// apply transformation to the geometry
void transform_geometry(const Complex &arg_trans_c, const char &arg_op);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
// Complex class implementation
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
// Copy constructor
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
// assignment operator
Complex &Complex::operator=(const Complex &arg_c)
{
if (this == &arg_c) // self-assignment
return *this;
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
// add assignment operator
Complex &Complex::operator+=(const Complex &arg_c)
{
m_real += arg_c.m_real;
m_imag += arg_c.m_imag;
return *this;
}
// multiply assignment operator
Complex &Complex::operator*=(const Complex &arg_c)
{
double real = m_real * arg_c.m_real - m_imag * arg_c.m_imag;
double imag = m_real * arg_c.m_imag + m_imag * arg_c.m_real;
m_real = real;
m_imag = imag;
return *this;
}
// length of the complex number
double Complex::length() const
{
return sqrt(m_real * m_real + m_imag * m_imag);
}
// angle of the complex number in radians
double Complex::angle() const
{
if (m_real == 0 && m_imag == 0)
{
return NAN;
}
return atan2(m_imag, m_real);
}
// cout `<<` operator for print complex number
// note: be careful about the format of output
ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag > 0)
{
arg_os << arg_c.m_real << " + " << arg_c.m_imag << "i";
}
else if (arg_c.m_imag < 0)
{
arg_os << arg_c.m_real << " - " << -arg_c.m_imag << "i";
}
else
{
arg_os << arg_c.m_real;
}
return arg_os;
}
// cin `>>` operator for input complex number
// note: be careful about the format of input
istream &operator>>(istream &arg_is, Complex &arg_c)
{
double input_real, input_imag;
arg_is >> input_real;
if (arg_is.fail())
{
error_and_exit();
}
arg_is >> input_imag;
if (arg_is.fail() || !arg_is.eof())
{
error_and_exit();
}
arg_c.m_real = input_real;
arg_c.m_imag = input_imag;
return arg_is;
}
// Geometry_Comp class implementation
// check if the transformation is valid
bool Geometry_Comp::_check_transform(const Complex &arg_c, const char &arg_op)
{
// check if the operation is valid
if (arg_op == 'r' && (arg_c.length() != 1 || isnan(arg_c.angle())))
{
return false;
}
else if (arg_op == 'z' && (arg_c.m_real == 0 || arg_c.m_imag != 0))
{
return false;
}
else
{
return true;
}
}
// Constructor, initializes the array
Geometry_Comp::Geometry_Comp(const unsigned int &arg_num_of_vertex)
: m_comp_array(arg_num_of_vertex)
{
}
// Copy constructor
Geometry_Comp::Geometry_Comp(const Geometry_Comp &arg_gc)
: m_comp_array(arg_gc.m_comp_array)
{
}
// assignment operator
Geometry_Comp &Geometry_Comp::operator=(const Geometry_Comp &arg_gc)
{
if (this == &arg_gc) // self-assignment
return *this;
m_comp_array = arg_gc.m_comp_array;
return *this;
}
// print the geometry
void Geometry_Comp::print_geometry()
{
cout << "not implemented" << endl;
}
// parse the cin to the geometry
void Geometry_Comp::parse_geometry(istream &arg_is)
{
cout << "not implemented" << endl;
}
// apply transformation to the geometry
void Geometry_Comp::transform_geometry(const Complex &arg_c, const char &arg_op)
{
if (!(_check_transform(arg_c, arg_op)))
{
error_and_exit();
}
if (arg_op == 'm')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] += arg_c;
}
}
else if (arg_op == 'r' || arg_op == 'z')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] *= arg_c;
}
}
}
// set the geometry
void Geometry_Comp::set_geometry(const vector<Complex> &arg_comp_array)
{
m_comp_array = arg_comp_array;
}
// get the geometry array
vector<Complex> Geometry_Comp::get_geometry_array()
{
return m_comp_array;
}
// Triangle_Comp class implementation
// Constructor, initializes the array
Triangle_Comp::Triangle_Comp()
: Geometry_Comp(triangle_num_of_vertex)
{
}
// Copy constructor
Triangle_Comp::Triangle_Comp(const Triangle_Comp &arg_tc)
: Geometry_Comp(arg_tc)
{
}
// assignment operator
Triangle_Comp &Triangle_Comp::operator=(const Triangle_Comp &arg_tc)
{
if (this == &arg_tc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_tc);
return *this;
}
// print the geometry
void Triangle_Comp::print_geometry()
{
cout << "t" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < triangle_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Triangle_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
stringstream ss(temp);
unsigned int vertex_num;
ss >> vertex_num;
if (vertex_num != triangle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Quadrilateral_Comp class implementation
// Constructor, initializes the array
Quadrilateral_Comp::Quadrilateral_Comp()
: Geometry_Comp(quadrilateral_num_of_vertex)
{
}
// Copy constructor
Quadrilateral_Comp::Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc)
: Geometry_Comp(arg_qc)
{
}
// assignment operator
Quadrilateral_Comp &Quadrilateral_Comp::operator=(const Quadrilateral_Comp &arg_qc)
{
if (this == &arg_qc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_qc);
return *this;
}
// print the geometry
void Quadrilateral_Comp::print_geometry()
{
cout << "q" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < quadrilateral_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Quadrilateral_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != quadrilateral_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Polygon_Comp class implementation
// Constructor, initializes the array
Polygon_Comp::Polygon_Comp()
: Geometry_Comp()
{
}
// Copy constructor
Polygon_Comp::Polygon_Comp(const Polygon_Comp &arg_pc)
: Geometry_Comp(arg_pc)
{
}
// assignment operator
Polygon_Comp &Polygon_Comp::operator=(const Polygon_Comp &arg_pc)
{
if (this == &arg_pc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_pc);
return *this;
}
// print the geometry
void Polygon_Comp::print_geometry()
{
cout << "p" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < m_comp_array.size(); i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Polygon_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num < triangle_num_of_vertex)
{
error_and_exit();
}
m_comp_array.resize(vertex_num);
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Circle_Comp class implementation
// Constructor, initializes the array
Circle_Comp::Circle_Comp()
: Geometry_Comp(circle_num_of_vertex)
{
}
// Copy constructor
Circle_Comp::Circle_Comp(const Circle_Comp &arg_cc)
: Geometry_Comp(arg_cc)
{
}
// assignment operator
Circle_Comp &Circle_Comp::operator=(const Circle_Comp &arg_cc)
{
if (this == &arg_cc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_cc);
return *this;
}
// print the geometry
void Circle_Comp::print_geometry()
{
cout << "c" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < circle_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Circle_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != circle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
int main()
{
string input, temp;
vector<Geometry_Comp *> geo_ptr_array;
Geometry_Comp *geo_ptr;
Complex trans_c;
char trans_op;
while (getline(cin, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
case 'r':
case 'z':
case 'm':
getline(cin, temp);
break;
default:
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
if (input[0] == 't' || input[0] == 'q' || input[0] == 'p' || input[0] == 'c')
{
// parse the cin to the geometry
geo_ptr->parse_geometry(cin);
// print the geometry
geo_ptr->print_geometry();
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else if (input[0] == 'r' || input[0] == 'z' || input[0] == 'm')
{
stringstream ss(temp);
ss >> trans_c;
// transform the geometry using operator and complex
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->transform_geometry(trans_c, input[0]);
// print transformed geometry
geo_ptr_array[i]->print_geometry();
}
}
else
{
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
}
return 0;
}
File Processing (1)
Slides version: lecture13_slides.html Website version: lecture13.html
- What is File?
- Temporary variable & Permanent file
- Example: Gradebook (Text) & Image (Binary)
- File 101 in C++
- Open & Close File
- Read or Write or Read & Write
- Text or Binary
- Append or Overwrite
- Sequantial or Random Access
- Example 1: Big Real Number in Text File
- Example 2: Point & Triangle in Text File (function ver.)
- Example 3: Vector & Matrix in Binary File (function ver.)
- Pratices
What is File?
A computer file is a computer resource for recording data in a computer storage device, primarily identified by its file name. Just as words can be written to paper, so can data be written to a computer file.
Ref: https://en.wikipedia.org/wiki/Computer_file

Example: Gradebook (Text)
In text format (csv):
Name,Grade
John,A
Mary,B
In table format:
| Name | Grade |
|---|---|
| John | A |
| Mary | B |
Example: Image (Binary)
In viewable format: as the image on the right

In binary format:
00000000: ffd8 ffe1 4812 4578 6966 0000 4d4d 002a ....H.Exif..MM.*
00000010: 0000 0008 0007 0112 0003 0000 0001 0001 ................
00000020: 0000 011a 0005 0000 0001 0000 0062 011b .............b..
00000030: 0005 0000 0001 0000 006a 0128 0003 0000 .........j.(....
00000040: 0001 0002 0000 0131 0002 0000 001c 0000 .......1........
00000050: 0072 0132 0002 0000 0014 0000 008e 8769 .r.2...........i
00000060: 0004 0000 0001 0000 00a4 0000 00d0 002d ...............-
00000070: c6c0 0000 2710 002d c6c0 0000 2710 4164 ....'..-....'.Ad
00000080: 6f62 6520 5068 6f74 6f73 686f 7020 4353 obe Photoshop CS
00000090: 3520 5769 6e64 6f77 7300 3230 3133 3a30 5 Windows.2013:0
000000a0: 343a 3031 2031 353a 3033 3a30 3400 0000 4:01 15:03:04...
000000b0: 0003 a001 0003 0000 0001 0001 0000 a002 ................
File 101 in C++
Steps to process a file:
- Open a file
- Seek to a position
- Read or write data
- Close the file
Open a file (Write)
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// write to a file
// create a output file stream object
ofstream outfile;
// open a file
outfile.open("test.txt");
// check if the file is open
if (!outfile)
{
cout << "Error opening file" << endl;
return 1;
}
// ...
}
Seek to a position (Write)
int main()
{
// ...
// open a file
outfile.open("test.txt");
// ...
// seek to the end of the file
outfile.seekp(0, ios::end);
// ...
}
test.txt:
|
Read or write data (Write)
int main()
{
// ...
// seek to the end of the file
outfile.seekp(0, ios::end);
// write to the file
outfile << "Hello World!" << endl;
// ...
}
test.txt:
Hello World!⏎
|
Close the file (Write)
int main()
{
// ...
// write to the file
outfile << "Hello World!" << endl;
// close the file
outfile.close();
}
test.txt:
Hello World!⏎
|<EOF>
Hello World! (Write)
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// write to a file
// create a output file stream object
ofstream outfile;
// open a file
outfile.open("test.txt");
// check if the file is open
if (!outfile)
{
cout << "Error opening file" << endl;
return 1;
}
// seek to the end of the file
outfile.seekp(0, ios::end);
// write to the file
outfile << "Hello World!" << endl;
// close the file
outfile.close();
}
Open a file (Read)
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// read from a file
// create a input file stream object
ifstream infile;
// open the file
infile.open("test.txt");
// or open the file with ifstream constructor
// ifstream infile("test.txt");
// check if the file is open
if(!infile)
{
cout << "Error opening file" << endl;
return -1;
}
// ...
}
Seek to a position (Read)
int main()
{
// ...
// open the file
infile.open("test.txt");
// ...
// seek to the front of the file
infile.seekg(0, ios::beg);
// ...
}
test.txt:
|Hello World!⏎
<EOF>
Read or write data (Read)
int main()
{
// ...
// seek to the front of the file
infile.seekg(0, ios::beg);
// read the file until the end (.eof() is true)
while(!infile.eof())
{
// read a line
string line;
getline(infile, line);
// print the line
cout << line << endl;
}
// ...
}
test.txt:
Hello World!⏎
|<EOF>
console:
$ ./a.out
Hello World!
$
Close the file (Write)
int main()
{
// ...
// read the file until the end (.eof() is true)
while(!infile.eof())
{
// read a line
string line;
getline(infile, line);
// print the line
cout << line << endl;
}
// close the file
infile.close();
}
Hello World! (Read)
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// read from a file
// create a input file stream object
ifstream infile;
// open the file
infile.open("test.txt");
// or open the file with ifstream constructor
// ifstream infile("test.txt");
// check if the file is open
if(!infile)
{
cout << "Error opening file" << endl;
return -1;
}
// seek to the front of the file
infile.seekg(0, ios::beg);
// read the file until the end (.eof() is true)
while(!infile.eof())
{
// read a line
string line;
getline(infile, line);
// print the line
cout << line << endl;
}
// close the file
infile.close();
}
Open & Close File
Three ways to open a file:
- Open a file with
ofstream(Write only) - Open a file with
ifstream(Read only) - Open a file with
fstream(Read & Write)
Two functions to open a file:
- Use constructor
fstream(filename, mode) - Use function
open(filename, mode)
To close a file:
- Use function
close() - Use destructor inplicitly
- The destructor will be called when the function returns
Open & Close a file with ofstream (Write only)
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a output file stream object
ofstream outfile;
// open a file with `.open(filename)`
outfile.open("test.txt");
// close the file
outfile.close();
// open a file with constructor `ofstream(filename)`
ofstream outfile2("test.txt");
// close the file
outfile2.close();
}
Open & Close a file with ifstream (Read only)
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object
ifstream infile;
// open a file with `.open(filename)`
infile.open("test.txt");
// close the file
infile.close();
// open a file with constructor `ifstream(filename)`
ifstream infile2("test.txt");
// close the file
infile2.close();
}
Open & Close a file with fstream (Read & Write)
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object
fstream file;
// open a file with `.open(filename)`
file.open("test.txt");
// close the file
file.close();
// open a file with constructor `fstream(filename)`
fstream file2("test.txt");
// close the file
file2.close();
}
Check if the file is open
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object
fstream file;
// open a file with `.open(filename)`
file.open("test.txt");
// check if the file is open
if(!file)
{
cout << "Error opening file" << endl;
return -1;
}
// or use `.is_open()`
if(!file.is_open())
{
cout << "Error opening file" << endl;
return -1;
}
// do something
// close the file
file.close();
}
Read or Write or Read & Write
- To read a file only: use
ifstreamorfstream(filename, ios::in) - To write a file only: use
ofstreamorfstream(filename, ios::out) - To read & write a file: use
fstream(filename, ios::in | ios::out)
Note:
ifstreamis used likefstream(filename, ios::in)but not the sameofstreamis used likefstream(filename, ios::out)but not the same
Read a file only
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object with `ifstream(filename)`
ifstream infile("test.txt");
// print the file
while(!infile.eof())
{
// read a line
string line;
getline(infile, line);
// print the line
cout << line << endl;
}
infile.close();
// or use `fstream(filename, ios::in)`
fstream file;
// open a file with `.open(filename)`
file.open("test.txt", ios::in);
// print the file
while(!file.eof())
{
string line;
getline(file, line);
cout << line << endl;
}
// close the file
file.close();
}
Write a file only
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a output file stream object with `ofstream(filename)`
ofstream outfile("test.txt");
// write a line
outfile << "Hello World!" << endl;
// close the file
outfile.close();
// or use `fstream(filename, ios::out)`
fstream file;
// open a file with `.open(filename)`
file.open("test2.txt", ios::out);
// write a line
file << "Hello World!" << endl;
// close the file
file.close();
}
Read & Write a file
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object with `fstream(filename, ios::in | ios::out)`
// Note: create "test.txt" first
fstream file("test.txt", ios::in | ios::out);
// write lines
for( int i = 0; i < 10; i++ )
{
file << "Line " << i << endl;
}
// seek to the beginning of the file
file.seekg(0, ios::beg);
// print the file
for( int i = 0; i < 10; i++ )
{
// read a line
string line;
getline(file, line);
// print the line
cout << line << endl;
}
// close the file
file.close();
}
If file not exist
fstream, ifstream and ofstream will handle the file if it not exist.
- Create new file:
ofstream,fstream(filename, ios::out),fstream(filename, ios::in | ios::out | ios::trunc),fstream(filename, ios::out | ios::app)ios::trunc&ios::appwill be disscussed later
- Error opening file:
ifstream,fstream(filename, ios::in),fstream(filename, ios::in | ios::out)
Example:
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// open a non-existing file
ifstream infile("test.txt");
// check if the file is open
if(!infile)
{
cout << "Error opening file" << endl;
}
// create a new file and open it
ofstream outfile("test.txt");
// write some text to the file
outfile << "Hello World!" << endl;
outfile.close();
// read the file again
fstream file("test.txt");
// check if the file is open
if(!file)
{
cout << "Error opening file" << endl;
}
// read the file
while (!file.eof())
{
string line;
getline(file, line);
cout << line << endl;
}
// close the file
file.close();
}
Text or Binary
- Text file: save the data in character format
Name,Grade
John,A
Mary,B
- Binary file: save the data with the same format as the computer
00000000: ffd8 ffe1 4812 4578 6966 0000 4d4d 002a ....H.Exif..MM.*
The file saved JPEG header ffd8, ffe1, and has 18,450 (0x4812) bytes of metadata.
The metadata store EXIF information Exif..MM.* (4578 6966 0000 4d4d 002a).
Read & Write a text file
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object with `fstream(filename, ios::in | ios::out)`
// Note: create "test.txt" first
fstream file("test.txt", ios::in | ios::out);
// write lines
for( int i = 0; i < 10; i++ )
{
file << "Line " << i << endl;
}
// seek to the beginning of the file
file.seekg(0, ios::beg);
// print the file
for( int i = 0; i < 10; i++ )
{
// read a line
string line;
getline(file, line);
// print the line
cout << line << endl;
}
// close the file
file.close();
}
Result: test.txt
Line 0⏎
Line 1⏎
Line 2⏎
Line 3⏎
Line 4⏎
Line 5⏎
Line 6⏎
Line 7⏎
Line 8⏎
Line 9⏎
<EOF>
Read & Write a binary file
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object with `fstream(filename, ios::in | ios::out)`
// Note: create "test.bin" first
fstream file("test.bin", ios::in | ios::out | ios::binary);
// write lines
for (int i = 0; i < 10; i++)
{
string temp("Line");
// write string to file, we need to use `.c_str()` to convert string to char*
file.write(temp.c_str(), temp.size());
// for other data type like int, float, double, etc.
// we need to convert the data type to char* first
// use `&` to get the address of the data,
// use `(char *)` to convert the address to char*,
// and use `sizeof(type)` to get the size (number of bytes) of the data type
// then use `.write(data, size)` to write the data to file
file.write((char *)&i, sizeof(int)); // write int value to file
}
file.flush(); // flush the buffer
// seek to the beginning of the file
file.seekg(0, ios::beg);
// print the file
for (int i = 0; i < 10; i++)
{
// read string from file
char temp[5];
// because we store "Line" in the file, so we only need to read 4 bytes
file.read(temp, 4);
// add '\0' to the end of the string
temp[4] = '\0';
// read int from file
int temp_int;
// same as write, we need to convert the data type to char* first
// then use `.read(data, size)` to read the data from file
file.read((char *)&temp_int, sizeof(int));
cout << temp << " " << temp_int << endl;
}
// close the file
file.close();
}
Result: test.bin
00000000: 4c69 6e65 0000 0000 4c69 6e65 0100 0000 Line....Line....
00000010: 4c69 6e65 0200 0000 4c69 6e65 0300 0000 Line....Line....
00000020: 4c69 6e65 0400 0000 4c69 6e65 0500 0000 Line....Line....
00000030: 4c69 6e65 0600 0000 4c69 6e65 0700 0000 Line....Line....
00000040: 4c69 6e65 0800 0000 4c69 6e65 0900 0000 Line....Line....
Append or Overwrite
Two ways to handle a existing file:
- Append (
ios::app): append the data to the end of the file - Overwrite (
ios::trunc): overwrite the file
Append (ios::app)
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object with `fstream(filename, ios::in | ios::out)`
// Note: create "test.txt" first
fstream file("test.txt", ios::in | ios::out);
// write lines
for (int i = 0; i < 10; i++)
{
file << "Line " << i << endl;
}
// seek to the beginning of the file
file.seekg(0, ios::beg);
// print the file
for (int i = 0; i < 10; i++)
{
// read a line
string line;
getline(file, line);
// print the line
cout << line << endl;
}
// close the file
file.close();
// open again with `ios::app`
fstream file2("test.txt", ios::in | ios::out | ios::app);
// write a line
for (int i = 10; i < 20; i++)
{
file2 << "Line " << i << endl;
}
// seek to the beginning of the file
file2.seekg(0, ios::beg);
// print the file
for (int i = 0; i < 20; i++)
{
// read a line
string line;
getline(file2, line);
// print the line
cout << line << endl;
}
// close the file
file2.close();
}
Result: test.txt
Line 0⏎
Line 1⏎
Line 2⏎
Line 3⏎
Line 4⏎
Line 5⏎
Line 6⏎
Line 7⏎
Line 8⏎
Line 9⏎
Line 10⏎
Line 11⏎
Line 12⏎
Line 13⏎
Line 14⏎
Line 15⏎
Line 16⏎
Line 17⏎
Line 18⏎
Line 19⏎
<EOF>
Overwrite (ios::trunc)
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object with `fstream(filename, ios::in | ios::out)`
// Note: create "test.txt" first
fstream file("test.txt", ios::in | ios::out);
// write lines
for (int i = 0; i < 10; i++)
{
file << "Line " << i << endl;
}
// seek to the beginning of the file
file.seekg(0, ios::beg);
// print the file
for (int i = 0; i < 10; i++)
{
// read a line
string line;
getline(file, line);
// print the line
cout << line << endl;
}
// close the file
file.close();
// open again with `ios::app`
fstream file2("test.txt", ios::in | ios::out | ios::trunc);
// write a line
for (int i = 10; i < 20; i++)
{
file2 << "Line " << i << endl;
}
// seek to the beginning of the file
file2.seekg(0, ios::beg);
// print the file
for (int i = 0; i < 20; i++)
{
// read a line
string line;
getline(file2, line);
// print the line
cout << line << endl;
}
// close the file
file2.close();
}
Result: test.txt
Line 10⏎
Line 11⏎
Line 12⏎
Line 13⏎
Line 14⏎
Line 15⏎
Line 16⏎
Line 17⏎
Line 18⏎
Line 19⏎
<EOF>
Sequantial or Random Access
By default, the file is sequantial access.
.tellp() and .tellg() can tell the current position of the file.
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object with `fstream(filename, ios::in | ios::out)`
// Note: create "test.txt" first
fstream file("test.txt", ios::in | ios::out);
// write lines
cout << file.tellp() << endl; // print the current position for `<<`
for (int i = 0; i < 10; i++)
{
file << "Line " << i << endl;
cout << file.tellp() << endl;
}
// seek to the beginning of the file
file.seekg(0, ios::beg);
// print the file
cout << file.tellg() << endl; // print the current position for `>>` and getline()
for (int i = 0; i < 10; i++)
{
// read a line
string line;
getline(file, line);
// print the line
cout << file.tellg() << " " << line << endl;
}
// close the file
file.close();
}
Result: terminal
0
7
14
21
28
35
42
49
56
63
70
0
7 Line 0
14 Line 1
21 Line 2
28 Line 3
35 Line 4
42 Line 5
49 Line 6
56 Line 7
63 Line 8
70 Line 9
Random Access
.seekp(pos) and .seekg(pos) can seek to the position of the file.
Three reference position:
ios::beg: the beginning of the fileios::cur: the current position of the fileios::end: the end of the file
// include iostream & fstream for handle the file object
#include <iostream>
#include <fstream>
// short-cut of std::
using namespace std;
int main()
{
// create a input file stream object with `fstream(filename, ios::in | ios::out)`
// Note: create "test.txt" first
fstream file("test.txt", ios::in | ios::out);
// write lines
cout << file.tellp() << endl; // print the current position for `<<`
for (int i = 0; i < 10; i++)
{
file << "Line " << i << endl;
cout << file.tellp() << endl;
}
// seek to the 5th line from the beginning
file.seekp(5 * 7, ios::beg);
cout << file.tellp() << endl; // print the current position for `<<`
for (int i = 15; i < 20; i++)
{
file << "Line " << i << endl;
cout << file.tellp() << endl;
}
// seek to the beginning of the file
file.seekg(0, ios::beg);
// or use `file.seekg(0);`
// print the file
cout << file.tellg() << endl; // print the current position for `>>` and getline()
for (int i = 0; i < 10; i++)
{
// seek to the 3th-previous line if read th 5th line
if (i == 5)
{
file.seekg(-3 * 7, ios::cur);
}
// read a line
string line;
getline(file, line);
// print the line
cout << file.tellg() << " " << line << endl;
}
// close the file
file.close();
}
Result: terminal
0
7
14
21
28
35
42
49
56
63
70
35
43
51
59
67
75
0
7 Line 0
14 Line 1
21 Line 2
28 Line 3
35 Line 4
21 Line 2
28 Line 3
35 Line 4
43 Line 15
51 Line 16
Summary of File I/O 101
- Open & Close File
- constructor or
.open()
- constructor or
- Read or Write or Read & Write
ifstreamandofstreamios::inandios::outinmodeargument offstream
- Text or Binary
ios::binaryinmodeargument
- Append or Overwrite
ios::appandios::truncinmodeargument
- Sequantial or Random Access
.seekp()and.tellp()for set/get position of<<.seekg()and.tellg()for set/get position of>>orgetline()
mode and file handeling
Ref: std::basic_filebuf<CharT,Traits>::open - cppreference.com
mode | Action if file exists | Action if file does not exist |
|---|---|---|
in | Read from start | Error |
out, out\|trunc | Destory contents | Create new |
app, out\|app | Write to end | Create new |
out\|in | Read from start | Error |
out\|in\|trunc | Destory contents | Create new |
out\|in\|app, in\|app | Write to end | Create new |
binray\|in | Read from start | Error |
binray\|out, binray\|out\|trunc | Destory contents | Create new |
binray\|app, binray\|out\|app | Write to end | Create new |
binray\|out\|in | Read from start | Error |
binray\|out\|in\|trunc | Destory contents | Create new |
binray\|out\|in\|app, binray\|in\|app | Write to end | Create new |
Example 1: Big Real Number in Text File [Source]
Ref: Lab 7: 真・大數四則運算 - Introduction to Programming (I)
Example 2: Point & Triangle in Text File (function ver.) [Source]
Example 3: Vector & Matrix in Binary File (function ver.) [Source]
Pratices
- Read & Write Point & Triangle in Binary File
- Read & Write Vector & Matrix in CSV format
- Seprator column by
, - Seprator row by
\n
- Seprator column by
Example 1: Big Real Number in Text File
#include <iostream>
#include <fstream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
char buffer[10001];
vector<int> a, b, c;
int n, a_sign = 1, b_sign = 1, c_sign = 1;
bool zero_start = true;
ofstream log_file("log.txt", ios::out | ios::app);
cout << "Big number calculator"
<< endl
<< "1) display only"
<< endl
<< "2) plus (+)"
<< endl
<< "3) minus (-)"
<< endl
<< "4) multiplication (*)"
<< endl
<< "5) division (/)"
<< endl
<< "Please select the operator: ";
cin >> buffer;
if (!isdigit(buffer[0]) || buffer[1] != '\0')
{
cout << "Invalid input: " << buffer << endl;
return 0;
}
n = buffer[0] - '0';
switch (n)
{
case 1:
cout << "You selected: display only" << endl;
break;
case 2:
cout << "You selected: +" << endl;
break;
case 3:
cout << "You selected: -" << endl;
break;
case 4:
cout << "You selected: *" << endl;
break;
case 5:
cout << "You selected: /" << endl;
break;
default:
cout << "Invalid input: " << buffer << endl;
return 0;
}
for (int i = 0; buffer[i] != '\0'; i++)
buffer[i] = '\0';
cout << "Input integer number (a): ";
cin >> buffer;
zero_start = true;
for (int i = 0; buffer[i] != '\0'; i++)
{
if (!isdigit(buffer[i]))
{
if (i == 0 && buffer[i] == '-')
{
a_sign = -1;
continue;
}
else
{
cout << "Invalid input: " << buffer << endl;
return 0;
}
}
if (buffer[i] == '0' && zero_start)
continue;
else
{
a.push_back((int)(buffer[i] - '0'));
zero_start = false;
}
}
if (a.empty())
{
a.push_back(0);
a_sign = 0;
}
reverse(a.begin(), a.end());
for (int i = 0; buffer[i] != '\0'; i++)
buffer[i] = '\0';
cout << "Input integer number (b): ";
cin >> buffer;
zero_start = true;
for (int i = 0; buffer[i] != '\0'; i++)
{
if (!isdigit(buffer[i]))
{
if (i == 0 && buffer[i] == '-')
{
b_sign = -1;
continue;
}
else
{
cout << "Invalid input: " << buffer << endl;
return 0;
}
}
if (buffer[i] == '0' && zero_start)
continue;
else
{
b.push_back((int)(buffer[i] - '0'));
zero_start = false;
}
}
if (b.empty())
{
if (n == 5)
{
cout << "Invalid input: " << buffer << endl;
return 0;
}
b.push_back(0);
b_sign = 0;
}
reverse(b.begin(), b.end());
cout << "(a) = " << (a_sign == -1 ? "-" : "");
for (int i = a.size() - 1; i >= 0; i--)
cout << a[i];
cout << '\n'
<< "(b) = " << (b_sign == -1 ? "-" : "");
for (int i = b.size() - 1; i >= 0; i--)
cout << b[i];
cout << endl;
// write to log file
log_file << "(a) = " << (a_sign == -1 ? "-" : "");
for (int i = a.size() - 1; i >= 0; i--)
log_file << a[i];
log_file << '\n'
<< "(b) = " << (b_sign == -1 ? "-" : "");
for (int i = b.size() - 1; i >= 0; i--)
log_file << b[i];
log_file << endl;
// Initialization Done
int carry = 0;
if (n == 1)
{
log_file.close();
return 0; // "Display only"
}
// "Display only" Done
else if (n == 2) // "+"
{
for (int i = 0; i < a.size() && i < b.size(); i++)
{
c.push_back((a[i] * a_sign + b[i] * b_sign + carry) % 10);
carry = (a[i] * a_sign + b[i] * b_sign + carry) / 10;
}
if (a.size() > b.size())
{
for (int i = b.size(); i < a.size(); i++)
{
c.push_back((a[i] * a_sign + carry) % 10);
carry = (a[i] * a_sign + carry) / 10;
}
}
else
{
for (int i = a.size(); i < b.size(); i++)
{
c.push_back((b[i] * b_sign + carry) % 10);
carry = (b[i] * b_sign + carry) / 10;
}
}
c.push_back(carry);
zero_start = true;
for (int i = c.size() - 1; i >= 0; i--)
{
if (c[i] == 0 && zero_start)
c.pop_back();
else
break;
}
if (c.empty())
c.push_back(0);
c_sign = (c[c.size() - 1] < 0 ? -1 : 1);
for (int i = 0; i < c.size(); i++)
{
if (c_sign * c[i] < 0)
{
c[i] += (10 * c_sign);
if (i + 1 < c.size())
c[i + 1] += (-1 * c_sign);
else
c.push_back(-1 * c_sign);
}
c[i] *= c_sign;
}
cout << "(a) + (b) = " << (c_sign < 0 ? "-" : "");
for (int i = c.size() - 1; i >= 0; i--)
cout << c[i];
cout << endl;
// write to log file
log_file << "(a) + (b) = " << (c_sign < 0 ? "-" : "");
for (int i = c.size() - 1; i >= 0; i--)
log_file << c[i];
log_file << endl;
log_file.close();
return 0;
}
// "+" Done
else if (n == 3) // "-"
{
for (int i = 0; i < a.size() && i < b.size(); i++)
{
c.push_back((a[i] * a_sign - b[i] * b_sign + carry) % 10);
carry = (a[i] * a_sign - b[i] * b_sign + carry) / 10;
}
if (a.size() > b.size())
{
for (int i = b.size(); i < a.size(); i++)
{
c.push_back((a[i] * a_sign + carry) % 10);
carry = (a[i] * a_sign + carry) / 10;
}
}
else
{
for (int i = a.size(); i < b.size(); i++)
{
c.push_back((-b[i] * b_sign + carry) % 10);
carry = (-b[i] * b_sign + carry) / 10;
}
}
c.push_back(carry);
zero_start = true;
for (int i = c.size() - 1; i >= 0; i--)
{
if (c[i] == 0 && zero_start)
c.pop_back();
else
break;
}
if (c.empty())
c.push_back(0);
c_sign = (c[c.size() - 1] < 0 ? -1 : 1);
for (int i = 0; i < c.size(); i++)
{
if (c_sign * c[i] < 0)
{
c[i] += (10 * c_sign);
if (i + 1 < c.size())
c[i + 1] += (-1 * c_sign);
else
c.push_back(-1 * c_sign);
}
c[i] *= c_sign;
}
cout << "(a) - (b) = " << (c_sign < 0 ? "-" : "");
for (int i = c.size() - 1; i >= 0; i--)
cout << c[i];
cout << endl;
// write to log file
log_file << "(a) - (b) = " << (c_sign < 0 ? "-" : "");
for (int i = c.size() - 1; i >= 0; i--)
log_file << c[i];
log_file << endl;
log_file.close();
return 0;
}
// "-" Done
else if (n == 4) // "*"
{
c_sign = a_sign * b_sign;
for (int i = 0; i < b.size(); i++)
{
for (int j = 0; j < a.size(); j++)
{
if (i + j >= c.size())
c.push_back(a[j] * b[i]);
else
c[i + j] += a[j] * b[i];
}
}
for (int i = 0; i < c.size(); i++)
{
carry += c[i];
c[i] = carry % 10;
carry /= 10;
}
c.push_back(carry);
zero_start = true;
for (int i = c.size() - 1; i >= 0; i--)
{
if (c[i] == 0 && zero_start)
c.pop_back();
else
break;
}
if (c.empty())
c.push_back(0);
cout << "(a) * (b) = " << (c_sign < 0 ? "-" : "");
for (int i = c.size() - 1; i >= 0; i--)
cout << c[i];
cout << endl;
// write to log file
log_file << "(a) * (b) = " << (c_sign < 0 ? "-" : "");
for (int i = c.size() - 1; i >= 0; i--)
log_file << c[i];
log_file << endl;
log_file.close();
return 0;
}
// "*" Done
else if (n == 5) // "/"
{
c_sign = a_sign * b_sign;
c.push_back(0);
while (a.size() >= b.size())
{
for (int i = 0; i < b.size(); i++)
{
carry += a[i] - b[i] + 10;
a[i] = carry % 10;
carry = carry / 10 - 1;
}
for (int i = b.size(); i < a.size(); i++)
{
if (carry == 0)
break;
carry += a[i] + 10;
a[i] = carry % 10;
carry = carry / 10 - 1;
}
a.push_back(carry);
zero_start = true;
for (int i = a.size() - 1; i >= 0; i--)
{
if (a[i] == 0 && zero_start)
a.pop_back();
else
break;
}
if (a.empty())
a.push_back(0);
if (a[a.size() - 1] >= 0)
c[0]++;
else
break;
}
cout << "(a) / (b) = " << (c_sign < 0 ? "-" : "") << c[0] << endl;
// write to log file
log_file << "(a) / (b) = " << (c_sign < 0 ? "-" : "") << c[0] << endl;
log_file.close();
return 0;
}
// "/" Done
return 0;
}
Example 2: Point & Triangle in Text File (function ver.)
#include <iostream>
#include <fstream>
using namespace std;
class Triangle_2D; // forward declaration
class Point_2D // the class name
// we use first upper case letter to indicate a class
{
private: // private data members & member functions
// Data members
// we use `m_` to indicate a data member
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// Member functions
// we use `_` to indicate a member function
// check if the point is valid
void _check_validity();
public: // public member functions
// Constructor
// Constructor & Default constructor
// initialize data members, with default values
// accessable to const object by default
Point_2D(const double &arg_x = 0, const double &arg_y = 0);
// Copy constructor
// copy the data members from the given object
// accessable to const object by default
Point_2D(const Point_2D &arg_point);
// Destructor
~Point_2D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// Member functions
// we use lower case letter to indicate a member function
// also, we just define the function declaration
// and leave the definition to the end of the class
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set(const double &arg_x, const double &arg_y);
// get the x coordinate and y coordinate
// accessable to const object
double get_x() const;
double get_y() const;
// // compare two points
bool operator==(const Point_2D &arg_point) const;
bool operator!=(const Point_2D &arg_point) const;
bool operator<(const Point_2D &arg_point) const;
bool operator>(const Point_2D &arg_point) const;
bool operator<=(const Point_2D &arg_point) const;
bool operator>=(const Point_2D &arg_point) const;
// assign the point with another point
Point_2D &operator=(const Point_2D &arg_point);
// friend class
friend class Triangle_2D;
// friend function
// print the x and y coordinate in format (x, y)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os, const Point_2D &arg_point);
// read the coordinate of a point from the input, format: (x, y) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Point_2D &arg_point);
};
// Triangle_2D class declaration
class Triangle_2D
{
private:
// define three points of the Triangle_2D
// in array of Point_2D format
Point_2D m_point[3];
// check & correct the Triangle_2D points to counterclockwise order
void _check_points();
public:
// Constructor
Triangle_2D(const double &arg_x0 = 0.0, const double &arg_y0 = 0.0,
const double &arg_x1 = 0.0, const double &arg_y1 = 0.0,
const double &arg_x2 = 0.0, const double &arg_y2 = 0.0);
// Copy constructor
Triangle_2D(const Triangle_2D &arg_triangle);
// Destructor
~Triangle_2D()
{
// do nothing
}
// modify the three points of the Triangle_2D
void set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2);
void set_point1(const double &arg_x0, const double &arg_y0);
void set_point2(const double &arg_x1, const double &arg_y1);
void set_point3(const double &arg_x2, const double &arg_y2);
void set_x0(const double &arg_x0);
void set_y0(const double &arg_y0);
void set_x1(const double &arg_x1);
void set_y1(const double &arg_y1);
void set_x2(const double &arg_x2);
void set_y2(const double &arg_y2);
// get the three points of the Triangle_2D
double get_x0() const;
double get_y0() const;
double get_x1() const;
double get_y1() const;
double get_x2() const;
double get_y2() const;
// calculate the area of the Triangle_2D
double area();
// print the Triangle_2D
// format: ((x0, y0), (x1, y1), (x2, y2))
friend std::ostream &operator<<(std::ostream &arg_os, const Triangle_2D &arg_tri);
// read the coordinate of a point from the input,
// format: ((x0, y0), (x1, y1), (x2, y2)) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Triangle_2D &arg_tri);
};
// function definition
// check if the point is valid
void Point_2D::_check_validity()
{
// check if the x coordinate is valid
if (m_x < 0)
{
// if not, set it to 0
m_x = 0;
}
// check if the y coordinate is valid
if (m_y < 0)
{
// if not, set it to 0
m_y = 0;
}
}
// Constructor & Default constructor
// initialize data members, with default values
Point_2D::Point_2D(const double &arg_x, const double &arg_y)
// use `: var_name1(arg_var_name1), var_name2(arg_var_name2)`
// to initialize data members
: m_x(arg_x),
m_y(arg_y)
{
// check if the point is valid
_check_validity();
}
// Copy constructor
// copy the data members from the given object
Point_2D::Point_2D(const Point_2D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y)
{
// check if the point is valid
_check_validity();
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_2D::set_x(const double &arg_x)
{
m_x = arg_x;
// check if the point is valid
_check_validity();
}
void Point_2D::set_y(const double &arg_y)
{
m_y = arg_y;
// check if the point is valid
_check_validity();
}
void Point_2D::set(const double &arg_x, const double &arg_y)
{
m_x = arg_x;
m_y = arg_y;
// check if the point is valid
_check_validity();
}
// get the x coordinate and y coordinate
// accessable to const object
double Point_2D::get_x() const
{
return m_x;
}
double Point_2D::get_y() const
{
return m_y;
}
// // compare two points
bool Point_2D::operator==(const Point_2D &arg_point) const
{
// if the x and y coordinates are equal,
// return true
return (m_x == arg_point.m_x && m_y == arg_point.m_y);
}
bool Point_2D::operator!=(const Point_2D &arg_point) const
{
return !(*this == arg_point);
}
bool Point_2D::operator<(const Point_2D &arg_point) const
{
// if the x coordinate is smaller than the other point,
// return true
if (m_x < arg_point.m_x)
{
return true;
}
// if the x coordinate is equal to the other point,
// check if the y coordinate is smaller than the other point
else if (m_x == arg_point.m_x)
{
// if the y coordinate is smaller, return true
if (m_y < arg_point.m_y)
{
return true;
}
// if the y coordinate is equal to the other point,
// return false
else if (m_y == arg_point.m_y)
{
return false;
}
// if the y coordinate is larger, return false
else
{
return false;
}
}
// if the x coordinate is larger, return false
else
{
return false;
}
}
bool Point_2D::operator>(const Point_2D &arg_point) const
{
return !(*this < arg_point || *this == arg_point);
}
bool Point_2D::operator<=(const Point_2D &arg_point) const
{
return (*this < arg_point || *this == arg_point);
}
bool Point_2D::operator>=(const Point_2D &arg_point) const
{
return !(*this < arg_point);
}
// assign the point with another point
Point_2D &Point_2D::operator=(const Point_2D &arg_point)
{
// check if the point is valid
_check_validity();
// assign the x and y coordinate
m_x = arg_point.m_x;
m_y = arg_point.m_y;
// check if the point is valid
_check_validity();
return *this;
}
// print the point in the format (x, y)
std::ostream &operator<<(std::ostream &arg_os, const Point_2D &arg_point)
{
arg_os << "(" << arg_point.m_x << ", " << arg_point.m_y << ")";
return arg_os;
}
// read the coordinate of a point from the input, format: (x, y) and ignore space
std::istream &operator>>(std::istream &arg_is, Point_2D &arg_point)
{
string str_x, str_y, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ')'))
{
arg_point.m_x = stod(str_x);
arg_point.m_y = stod(str_y);
}
}
}
// check if the point is valid
arg_point._check_validity();
return arg_is;
}
// Triangle_2D class implementation
// check & correct the Triangle_2D points to counterclockwise order
void Triangle_2D::_check_points()
{
// sort the points in ascending order
for (int i = 0; i < 3; i++)
{
for (int j = i + 1; j < 3; j++)
{
if (m_point[i] > m_point[j])
{
// swap the points
Point_2D temp = m_point[i];
m_point[i] = m_point[j];
m_point[j] = temp;
}
}
}
// if the area is negative, swap the points
if (area() < 0.0)
{
Point_2D temp = m_point[0];
m_point[0] = m_point[1];
m_point[1] = temp;
}
}
// Constructor
Triangle_2D::Triangle_2D(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
: m_point{Point_2D(arg_x0, arg_y0),
Point_2D(arg_x1, arg_y1),
Point_2D(arg_x2, arg_y2)} // init the array with {}
{
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// Copy constructor
Triangle_2D::Triangle_2D(const Triangle_2D &arg_triangle)
: m_point{Point_2D(arg_triangle.m_point[0]),
Point_2D(arg_triangle.m_point[1]),
Point_2D(arg_triangle.m_point[2])} // init the array with {}
{
}
// set the three points of the Triangle_2D
void Triangle_2D::set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
{
m_point[0].set(arg_x0, arg_y0);
m_point[1].set(arg_x1, arg_y1);
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point1(const double &arg_x0, const double &arg_y0)
{
m_point[0].set(arg_x0, arg_y0);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point2(const double &arg_x1, const double &arg_y1)
{
m_point[1].set(arg_x1, arg_y1);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point3(const double &arg_x2, const double &arg_y2)
{
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x0(const double &arg_x0)
{
m_point[0].m_x = arg_x0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y0(const double &arg_y0)
{
m_point[0].m_y = arg_y0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x1(const double &arg_x1)
{
m_point[1].m_x = arg_x1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y1(const double &arg_y1)
{
m_point[1].m_y = arg_y1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x2(const double &arg_x2)
{
m_point[2].m_x = arg_x2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y2(const double &arg_y2)
{
m_point[2].m_y = arg_y2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// get the three points of the Triangle_2D
double Triangle_2D::get_x0() const
{
return m_point[0].m_x;
}
double Triangle_2D::get_y0() const
{
return m_point[0].m_y;
}
double Triangle_2D::get_x1() const
{
return m_point[1].m_x;
}
double Triangle_2D::get_y1() const
{
return m_point[1].m_y;
}
double Triangle_2D::get_x2() const
{
return m_point[2].m_x;
}
double Triangle_2D::get_y2() const
{
return m_point[2].m_y;
}
// calculate the area of the Triangle_2D
double Triangle_2D::area()
{
// calculate the area of the Triangle_2D
return (m_point[0].m_x * m_point[1].m_y +
m_point[1].m_x * m_point[2].m_y +
m_point[2].m_x * m_point[0].m_y -
m_point[0].m_x * m_point[2].m_y -
m_point[1].m_x * m_point[0].m_y -
m_point[2].m_x * m_point[1].m_y) /
2.0;
}
// print the Triangle_2D
// format: ((x0, y0), (x1, y1), (x2, y2))
std::ostream &operator<<(std::ostream &arg_os, const Triangle_2D &arg_tri)
{
arg_os << "(";
for (int i = 0; i < 3; i++)
{
arg_os << arg_tri.m_point[i];
if (i < 2)
arg_os << ", ";
}
arg_os << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: ((x0, y0), (x1, y1), (x2, y2)) and ignore space
std::istream &operator>>(std::istream &arg_is, Triangle_2D &arg_tri)
{
string temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
for (int i = 0; i < 3; i++)
{
arg_is >> arg_tri.m_point[i];
if (i < 2)
{
getline(arg_is, temp, ','); // ignore the ','
}
}
getline(arg_is, temp, ')'); // ignore the last ')'
}
// check & correct the Triangle_2D points to counterclockwise order
arg_tri._check_points();
return arg_is;
}
// main function
int main()
{
Triangle_2D t(1, 1, 2, 2, 0, 3);
cout << t << endl;
cout << "Area: " << t.area() << endl;
ofstream t_file("triangle.txt", ios::out | ios::trunc);
// reuse the `<<` operator to write the Triangle_2D to the file
t_file << t << endl;
t_file.close();
// read the Triangle_2D from the file
ifstream t_file_in("triangle.txt", ios::in);
Triangle_2D t_in;
t_file_in >> t_in;
cout << t_in << endl;
cout << "Area: " << t_in.area() << endl;
t_file_in.close();
return 0;
}
Example 3: Vector & Matrix in Binary File (function ver.)
#include <iostream>
#include <fstream>
#include <cmath>
using namespace std;
class Vector_3D; // forward declaration
class Point_3D // represents a point in 3D space
{
private:
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// record the z coordinate
double m_z;
public:
Point_3D(const double &arg_x = 0, const double &arg_y = 0,
const double &arg_z = 0);
Point_3D(const Point_3D &arg_point);
// Destructor
~Point_3D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// modify the x, y and z coordinate
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
void set(const double &arg_x, const double &arg_y, const double &arg_z);
// get the x, y and z coordinate
double get_x() const;
double get_y() const;
double get_z() const;
// calculate the distance between two points
// in form of a vector
Vector_3D operator-(const Point_3D &arg_point) const;
// friend class
friend class Vector_3D;
// print the x and y coordinate in format (x, y, z)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os, const Point_3D &arg_point);
// read the coordinate of a point from the input,
// format: (x, y, z) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Point_3D &arg_point);
};
// Vector_3D class declaration
class Vector_3D
{
private:
// define the three factor of the basis vectors
// on the x, y, z axes
double m_x, m_y, m_z;
public:
// Constructor
Vector_3D(const double &arg_x = 0.0, const double &arg_y = 0.0,
const double &arg_z = 0.0);
Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2);
// Copy constructor
Vector_3D(const Vector_3D &arg_vector);
// Destructor
~Vector_3D()
{
// do nothing
}
// set the three factor of the basis vectors
void set_vector(const double &arg_x, const double &arg_y,
const double &arg_z);
void set_vector(const Point_3D &arg_point1, const Point_3D &arg_point2);
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
// get the three factor of the basis vectors
double get_x() const;
double get_y() const;
double get_z() const;
// assign operator
Vector_3D &operator=(const Vector_3D &arg_vector);
// calculate the length of the Vector_3D
double length();
// calculate the dot product of two vectors
int dot(const Vector_3D &);
// calculate the cross product of two vectors
Vector_3D cross(const Vector_3D &);
// print the Vector_3D in format (x, y, z)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os,
const Vector_3D &arg_point);
// read the factors of a vector from the input,
// format: (x, y, z) and ignore space
friend std::istream &operator>>(std::istream &arg_is,
Vector_3D &arg_point);
// write the Vector_3D in binary format
friend void write_vector_binary(std::ofstream &arg_ofs,
const Vector_3D &arg_vector);
// read the Vector_3D in binary format
friend void read_vector_binary(std::ifstream &arg_ifs,
Vector_3D &arg_vector);
};
// Point_3D class implementation
// Constructor & Default constructor
// initialize data members, with default values
Point_3D::Point_3D(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x),
m_y(arg_y),
m_z(arg_z)
{
}
// Copy constructor
// copy the data members from the given object
Point_3D::Point_3D(const Point_3D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y),
m_z(arg_point.m_z)
{
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_3D::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Point_3D::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Point_3D::set(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
// get the x coordinate and y coordinate
// accessable to const object
double Point_3D::get_x() const
{
return m_x;
}
double Point_3D::get_y() const
{
return m_y;
}
double Point_3D::get_z() const
{
return m_z;
}
// calculate the distance between two points
// in form of a vector
Vector_3D Point_3D::operator-(const Point_3D &arg_point) const
{
return Vector_3D(*this, arg_point);
}
// print the point in the format (x, y, z)
std::ostream &operator<<(std::ostream &arg_os, const Point_3D &arg_point)
{
arg_os << "(" << arg_point.m_x << ", " << arg_point.m_y
<< ", " << arg_point.m_z << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: (x, y, z) and ignore space
std::istream &operator>>(std::istream &arg_is, Point_3D &arg_point)
{
string str_x, str_y, str_z, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ','))
{
if (getline(arg_is, str_z, ')'))
{
arg_point.m_x = stod(str_x);
arg_point.m_y = stod(str_y);
arg_point.m_z = stod(str_z);
}
}
}
}
return arg_is;
}
// Vector_3D class implementation
// Constructor
Vector_3D::Vector_3D(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x), m_y(arg_y), m_z(arg_z)
{
}
Vector_3D::Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2)
: m_x(arg_point2.m_x - arg_point1.m_x),
m_y(arg_point2.m_y - arg_point1.m_y),
m_z(arg_point2.m_z - arg_point1.m_z)
{
}
// Copy constructor
Vector_3D::Vector_3D(const Vector_3D &arg_vector)
: m_x(arg_vector.m_x), m_y(arg_vector.m_y), m_z(arg_vector.m_z)
{
}
// set the three factor of the basis vectors
void Vector_3D::set_vector(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
void Vector_3D::set_vector(const Point_3D &arg_point1,
const Point_3D &arg_point2)
{
m_x = arg_point2.m_x - arg_point1.m_x;
m_y = arg_point2.m_y - arg_point1.m_y;
m_z = arg_point2.m_z - arg_point1.m_z;
}
void Vector_3D::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Vector_3D::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Vector_3D::set_z(const double &arg_z)
{
m_z = arg_z;
}
// get the three factor of the basis vectors
double Vector_3D::get_x() const
{
return m_x;
}
double Vector_3D::get_y() const
{
return m_y;
}
double Vector_3D::get_z() const
{
return m_z;
}
// assign operator
Vector_3D &Vector_3D::operator=(const Vector_3D &arg_vector)
{
m_x = arg_vector.m_x;
m_y = arg_vector.m_y;
m_z = arg_vector.m_z;
return *this;
}
// calculate the length of the Vector_3D
double Vector_3D::length()
{
// calculate the length of the Vector_3D
return sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
}
// calculate the dot product of two vectors
int Vector_3D::dot(const Vector_3D &arg_v)
{
// calculate the dot product of two vectors
return m_x * arg_v.m_x + m_y * arg_v.m_y + m_z * arg_v.m_z;
}
// calculate the cross product of two vectors
Vector_3D Vector_3D::cross(const Vector_3D &arg_v)
{
// calculate the cross product of two vectors
Vector_3D v;
v.m_x = m_y * arg_v.m_z - m_z * arg_v.m_y;
v.m_y = m_z * arg_v.m_x - m_x * arg_v.m_z;
v.m_z = m_x * arg_v.m_y - m_y * arg_v.m_x;
return v;
}
// print the point in the format (x, y, z)
std::ostream &operator<<(std::ostream &arg_os, const Vector_3D &arg_vector)
{
arg_os << "(" << arg_vector.m_x << ", " << arg_vector.m_y
<< ", " << arg_vector.m_z << ")";
return arg_os;
}
// read the factors of a vector from the input,
// format: (x, y, z) and ignore space
std::istream &operator>>(std::istream &arg_is, Vector_3D &arg_vector)
{
string str_x, str_y, str_z, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ','))
{
if (getline(arg_is, str_z, ')'))
{
arg_vector.m_x = stod(str_x);
arg_vector.m_y = stod(str_y);
arg_vector.m_z = stod(str_z);
}
}
}
}
return arg_is;
}
// write the vector to the file in binary format
void write_vector_binary(std::ofstream &arg_ofs, const Vector_3D &arg_vector)
{
arg_ofs.write((char *)&arg_vector.m_x, sizeof(double));
arg_ofs.write((char *)&arg_vector.m_y, sizeof(double));
arg_ofs.write((char *)&arg_vector.m_z, sizeof(double));
}
// read the vector from the file in binary format
void read_vector_binary(std::ifstream &arg_ifs, Vector_3D &arg_vector)
{
arg_ifs.read((char *)&arg_vector.m_x, sizeof(double));
arg_ifs.read((char *)&arg_vector.m_y, sizeof(double));
arg_ifs.read((char *)&arg_vector.m_z, sizeof(double));
}
// main function
int main()
{
Vector_3D v1(1, 2, 3);
Vector_3D v2(4, 5, 6);
cout << "v1 = " << v1 << endl;
cout << "v2 = " << v2 << endl;
// save the vector to the file in binary format
ofstream ofs("vector.bin", ios::binary | ios::trunc);
write_vector_binary(ofs, v1);
write_vector_binary(ofs, v2);
ofs.close();
// read the vector from the file in binary format
ifstream ifs("vector.bin", ios::binary);
Vector_3D v3, v4;
read_vector_binary(ifs, v3);
read_vector_binary(ifs, v4);
cout << "v3 = " << v3 << endl;
cout << "v4 = " << v4 << endl;
return 0;
}
File Processing (2)
Slides version: lecture14_slides.html Website version: lecture14.html
- Recap: File in C++
- Open & Close File
- Read or Write or Read & Write
- Text or Binary
- Append or Overwrite
- Sequantial or Random Access
- Detail in
iostream&fstream- Stream I/O & Buffer
- Stream Operator & Manipulator
- Stream Status & Error Handling (More details in lecture 15)
- File I/O &
class- File I/O function in a
class
- File I/O function in a
- File I/O for Structured Data
- Class or Function?
- Text or Binary File?
- Sequential or Random Access?
- Example 1: Point & Triangle in Text File (class ver.)
- Example 2: Vector & Matrix in Binary File (class ver.)
- Lab 14: File Export of Complex Number's Geometry
Recap: File in C++
Example: Gradebook (Text)
In text format (csv):
Name,Grade
John,A
Mary,B
In table format:
| Name | Grade |
|---|---|
| John | A |
| Mary | B |
Example: Image (Binary)
In viewable format: as the image on the right

In binary format:
00000000: ffd8 ffe1 4812 4578 6966 0000 4d4d 002a ....H.Exif..MM.*
00000010: 0000 0008 0007 0112 0003 0000 0001 0001 ................
00000020: 0000 011a 0005 0000 0001 0000 0062 011b .............b..
00000030: 0005 0000 0001 0000 006a 0128 0003 0000 .........j.(....
00000040: 0001 0002 0000 0131 0002 0000 001c 0000 .......1........
00000050: 0072 0132 0002 0000 0014 0000 008e 8769 .r.2...........i
00000060: 0004 0000 0001 0000 00a4 0000 00d0 002d ...............-
00000070: c6c0 0000 2710 002d c6c0 0000 2710 4164 ....'..-....'.Ad
00000080: 6f62 6520 5068 6f74 6f73 686f 7020 4353 obe Photoshop CS
00000090: 3520 5769 6e64 6f77 7300 3230 3133 3a30 5 Windows.2013:0
000000a0: 343a 3031 2031 353a 3033 3a30 3400 0000 4:01 15:03:04...
000000b0: 0003 a001 0003 0000 0001 0001 0000 a002 ................
Process a File
- Open & Close File
- constructor or
.open()
- constructor or
- Read or Write or Read & Write
ifstreamandofstreamios::inandios::outinmodeargument offstream
- Text or Binary
ios::binaryinmodeargument
- Append or Overwrite
ios::appandios::truncinmodeargument
- Sequantial or Random Access
.seekp()and.tellp()for set/get position of<<.seekg()and.tellg()for set/get position of>>orgetline()
mode and file handeling
Ref: std::basic_filebuf<CharT,Traits>::open - cppreference.com
mode | Action if file exists | Action if file does not exist |
|---|---|---|
in | Read from start | Error |
out, out\|trunc | Destory contents | Create new |
app, out\|app | Write to end | Create new |
out\|in | Read from start | Error |
out\|in\|trunc | Destory contents | Create new |
out\|in\|app, in\|app | Write to end | Create new |
binray\|in | Read from start | Error |
binray\|out, binray\|out\|trunc | Destory contents | Create new |
binray\|app, binray\|out\|app | Write to end | Create new |
binray\|out\|in | Read from start | Error |
binray\|out\|in\|trunc | Destory contents | Create new |
binray\|out\|in\|app, binray\|in\|app | Write to end | Create new |
Detail in iostream & fstream
Inheritance diagram: (Ref: File Handling through C++ Classes)
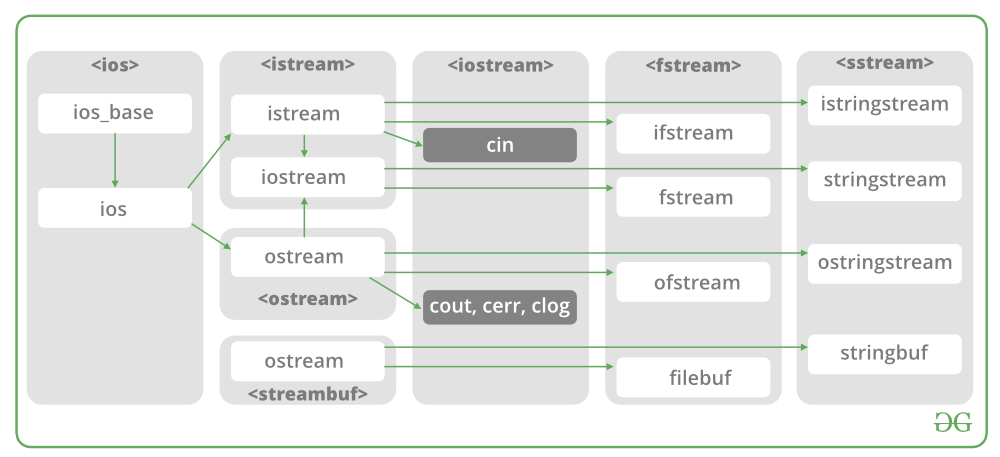
Some istream and ostream functions can be used in thier derived classes:
<<fromostreamand>>fromistreamcan be used infstreamandstringstreamput()fromostream,get()andgetline()fromistreamcan be used infstreamandstringstream- Manupulators, such as
std::fixed,std::setprecision()can be used infstreamandstringstream
Details will be discussed in lecture 15.
Stream I/O & Buffer
Ref: Basic Input / Output in C++
C++ comes with libraries that provide for performing input and output.
- Input Stream: The information is from the device (for example, Keyboard) to the main memory
- Output Stream: The information is from main memory to device (display screen)
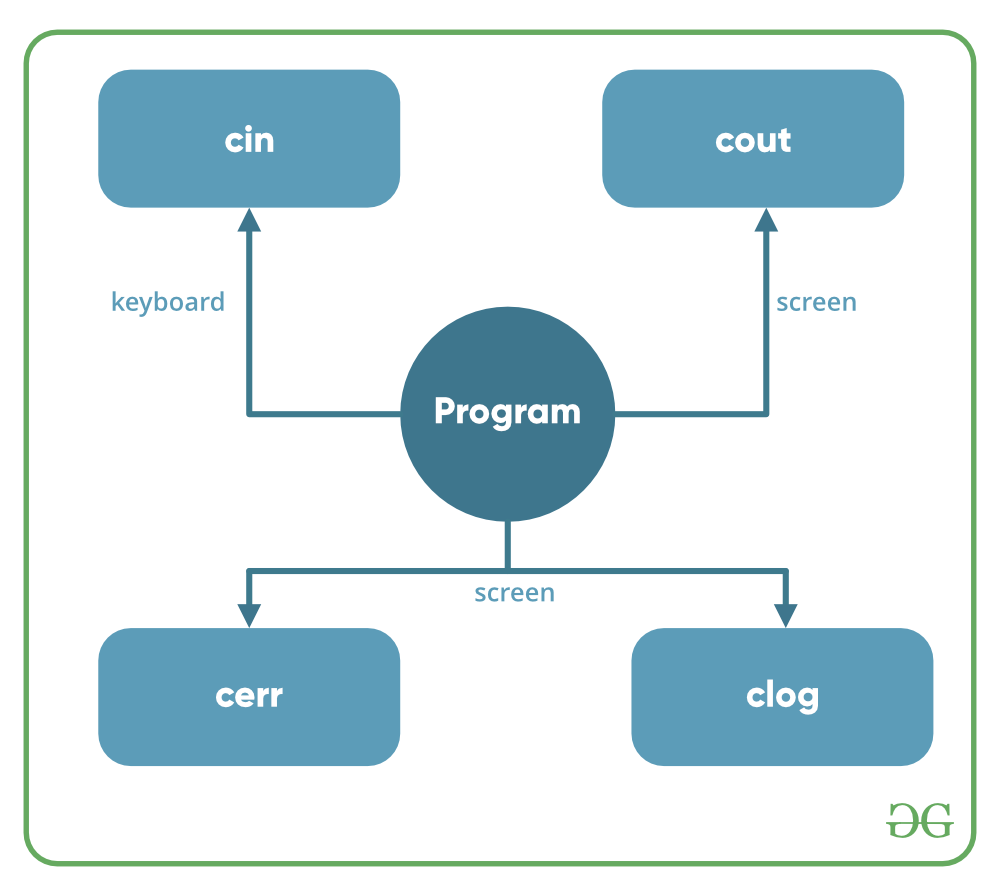
What is a buffer?
Ref: Clearing The Input Buffer In C/C++
A temporary storage area is called a buffer. All standard input and output devices contain an input and output buffer. In standard C/C++, streams are buffered, for example in the case of standard input, when we press the key on the keyboard, it isn’t sent to your program, rather it is buffered by the operating system till the time is allotted to that program.
Example:
// C++ Code to explain why
// not clearing the input
// buffer causes undesired
// outputs
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int a;
char ch[80];
// Enter input from user
// - 4 for example
cin >> a;
// Get input from user -
// "GeeksforGeeks" for example
cin.getline(ch, 80);
// Prints 4
cout << a << endl;
// Printing string : This does
// not print string
cout << ch << endl;
return 0;
}
Console:
$ ./a.out
4
GeeksforGeeks
4
$
Why? because the '\n' character is typed into the buffer and is not removed.
- When the user presses the Enter key, the '\n' character sends to the buffer.
How to clear the buffer?
- Using
cin.ignore(numeric_limits::max(),’\n’);
// C++ Code to explain how
// "cin.ignore(numeric_limits
// <streamsize>::max(),'\n');"
// discards the input buffer
#include <iostream>
// for <streamsize>
#include <ios>
// for numeric_limits
#include <limits>
using namespace std;
int main()
{
int a;
char str[80];
// Enter input from user
// - 4 for example
cin >> a;
// discards the input buffer
cin.ignore(numeric_limits<streamsize>::max(), '\n');
// Get input from user -
// GeeksforGeeks for example
cin.getline(str, 80);
// Prints 4
cout << a << endl;
// Printing string : This
// will print string now
cout << str << endl;
return 0;
}
- Using
cin.sync()
// C++ Code to explain how " cin.sync();"
// discards the input buffer
#include <iostream>
#include <ios>
#include <limits>
using namespace std;
int main()
{
int a;
char str[80];
// Enter input from user
// - 4 for example
cin >> a;
// Discards the input buffer
cin.sync();
// Get input from user -
// GeeksforGeeks for example
cin.getline(str, 80);
// Prints 4
cout << a << endl;
// Printing string - this
// will print string now
cout << str << endl;
return 0;
}
- Using
cin >> ws
// C++ Code to explain how "cin >> ws"
// discards the input buffer along with
// initial white spaces of string
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int a;
string s;
// Enter input from user -
// 4 for example
cin >> a;
// Discards the input buffer and
// initial white spaces of string
cin >> ws;
// Get input from user -
// GeeksforGeeks for example
getline(cin, s);
// Prints 4 and GeeksforGeeks :
// will execute print a and s
cout << a << endl;
cout << s << endl;
return 0;
}
Stream Operator & Manipulator
<< & >> stream operator
Overloading stream insertion (<>) operators in C++
- Why these operators must be overloaded as global? In operator overloading, if an operator is overloaded as a member, then it must be a member of the object on the left side of the operator. For example,
ob1 + ob2. To make this statement compile, we must overload+in a class ofob1or make+a global function. The operators<<and>>are called likecout << ob1andcin >> ob1. So if we want to make them a member method, then they must be made members of ostream and istream classes, which is not a good option most of the time. Therefore, these operators are overloaded as global functions with two parameters, cout and object of user-defined class.
Stream Manipulator (More detailed in lecture 15)
Ref: Manipulators in C++ with Examples
There are two types of manipulators in C++:
- Manipulators without arguments:
- endl: Defined in ostream. It is used to enter a new line and after entering a new line it flushes the output stream.
- ws: It is defined in istream and is used to ignore the whitespaces in the string sequence.
- ends: It is also defined in ostream and it inserts a null character into the output stream.
- flush: It is also defined in ostream and it flushes the output stream.
Example:
#include <iostream>
#include <istream>
#include <sstream>
#include <string>
using namespace std;
int main()
{
istringstream str(" Programmer");
string line;
// Ignore all the whitespace in string
// str before the first word.
getline(str >> std::ws, line);
// you can also write str>>ws
// After printing the output it will automatically
// write a new line in the output stream.
cout << line << endl;
// without flush, the output will be the same.
cout << "only a test" << flush;
// Use of ends Manipulator
cout << "\na";
// NULL character will be added in the Output
cout << "b" << ends;
cout << "c" << endl;
return 0;
}
- Manipulators with Arguments: Some of the manipulators are used with the argument like
setw(20),setfill(*), and many more.
- In
<iomanip>:setw(val),setfill(c),setprecision(val),setbase(val),setiosflags(flag),resetiosflags(m)
- In
<ios>:showpos,noshowpos,showbase,uppercase,nouppercase,fixed,scientific,hex,dec,oct,left,right
We will discuss the manipulators in the lecture 15.
Stream Status & Error Handling (More details in lecture 15)
Ref: std::basic_ios, std::ios_base::iostate
- 4 states:
.good(),.eof(),.fail(),.bad().good(): checks if no error has occurred i.e. I/O operations are available..eof(): checks if end-of-file has been reached..fail(): checks if an error has occurred..bad(): checks if a non-recoverable error has occurred.
all of them are based on ios_base::iostate
badbit:trueif the stream has an irrecoverable stream erroreofbit:trueif the stream's associated input sequence has reached end-of-filefailbit:trueif the stream has an input/output operation failed (formatting or extraction error)
Example
Ref: std::basic_ios<CharT,Traits>::good
#include <iostream>
#include <fstream>
#include <cstdlib>
int main()
{
const char *fname = "test.txt";
std::ofstream ofile{fname};
ofile << "10 "
<< "11 "
<< "12 "
<< "non-int";
ofile.close();
std::ifstream file{fname};
if (!file.good())
{
std::cout << "#1. Opening file test.txt failed - "
"one of the error flags is true\n";
return EXIT_FAILURE;
}
// typical C++ I/O loop uses the return value of the I/O function
// as the loop controlling condition, operator bool() is used here
for (int n; file >> n;)
{
std::cout << n << ' ';
}
std::cout << '\n';
if (file.bad())
{
std::cout << "#2. I/O error while reading - badbit is true\n";
return EXIT_FAILURE;
}
else if (file.eof())
{
std::cout << "#3. End of file reached successfully - eofbit is true\n"
"This is fine even though file.good() is false\n";
}
else if (file.fail())
{
std::cout << "#4. Non-integer data encountered - failbit is true\n";
}
}
Output:
$ ./a.out
10 11 12
#4. Non-integer data encountered - failbit is true
$
File I/O & class
File I/O function in a class
If we want to store the data of a class into a file, we can use 2 methods:
- Text File:
<<and>>operators - Binary File: new member functions
Text File
As we know, we can use << and >> operators to store and retrieve data from a file.
Just like we can use cout and cin to store and retrieve data from the console, we can use ofstream and ifstream to store and retrieve data from a file.
Binary File: new member functions
We can add new member functions to the class to store and retrieve binary data from a file. Two data styles:
- Read/Write each data member into a file
- Disscuss in example 2
- Read/Write the entire class variable into a file
Read/Write the entire class variable into a file
Ref: Read/Write Class Objects from/to File in C++
Theory:
The data transfer is usually done using >> and << operators.
But if you have a class with 4 data members and want to write all 4 data members from its object directly to a file or vice-versa, we can do that using following syntax:
To write object's data members in a file:
// Here file_obj is an object of ofstream
file_obj.write((char *) & class_obj, sizeof(class_obj));
To read file's data members into an object:
// Here file_obj is an object of ifstream
file_obj.read((char *) & class_obj, sizeof(class_obj));
Example:
// C++ program to demonstrate read/write of class
// objects in C++.
#include <iostream>
#include <fstream>
using namespace std;
// Class to define the properties
class Contestant
{
public:
// Instance variables
string Name;
int Age, Ratings;
// Function declaration of input() to input info
int input();
// Function declaration of output_highest_rated() to
// extract info from file Data Base
int output_highest_rated();
};
// Function definition of input() to input info
int Contestant::input()
{
// Object to write in file
ofstream file_obj;
// Opening file in append mode
file_obj.open("Input.txt", ios::app);
// Object of class contestant to input data in file
Contestant obj;
// Feeding appropriate data in variables
string str = "Michael";
int age = 18, ratings = 2500;
// Assigning data into object
obj.Name = str;
obj.Age = age;
obj.Ratings = ratings;
// Writing the object's data in file
file_obj.write((char *)&obj, sizeof(obj));
// Feeding appropriate data in variables
str = "Terry";
age = 21;
ratings = 3200;
// Assigning data into object
obj.Name = str;
obj.Age = age;
obj.Ratings = ratings;
// Writing the object's data in file
file_obj.write((char *)&obj, sizeof(obj));
return 0;
}
// Function definition of output_highest_rated() to
// extract info from file Data Base
int Contestant::output_highest_rated()
{
// Object to read from file
ifstream file_obj;
// Opening file in input mode
file_obj.open("Input.txt", ios::in);
// Object of class contestant to input data in file
Contestant obj;
// Reading from file into object "obj"
file_obj.read((char *)&obj, sizeof(obj));
// max to store maximum ratings
int max = 0;
// Highest_rated stores the name of highest rated contestant
string Highest_rated;
// Checking till we have the feed
while (!file_obj.eof())
{
// Assigning max ratings
if (obj.Ratings > max)
{
max = obj.Ratings;
Highest_rated = obj.Name;
}
// Checking further
file_obj.read((char *)&obj, sizeof(obj));
}
// Output is the highest rated contestant
cout << Highest_rated;
return 0;
}
// Driver code
int main()
{
// Creating object of the class
Contestant object;
// Inputting the data
object.input();
// Extracting the max rated contestant
object.output_highest_rated();
return 0;
}
File I/O for Structured Data
Guideline for Structured Data's File I/O:
- Class or Function?
- Depending on the data structure, we can either use a class or a function to read/write the data.
- If the data structure is a class, we can use the class's member functions to read/write the data.
- Otherwise, we can use a function to read/write the data.
- Text or Binary File?
- Binary file is used for efficient data transfer, but it is not human readable/editable.
- Text file is human readable/editable, but it is not efficient for large data transfer.
- Sequential or Random Access?
- Sequential access does not require large memory to store the data. Usually used for data parsing and processing.
- Random access requires large memory to store the data. Usually used for data storage, data retrieval, and data editing.
- Random access is faster than sequential access, especially for binary file.
Example 1: Point & Triangle in Text File (class ver.) [Source]
Example 2: Vector & Matrix in Binary File (class ver.) [Source]
Lab 14: File Export of Complex Number's Geometry
Example 1: Point & Triangle in Text File (class ver.)
#include <iostream>
#include <fstream>
using namespace std;
class Triangle_2D; // forward declaration
class Point_2D // the class name
// we use first upper case letter to indicate a class
{
private: // private data members & member functions
// Data members
// we use `m_` to indicate a data member
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// Member functions
// we use `_` to indicate a member function
// check if the point is valid
void _check_validity();
public: // public member functions
// Constructor
// Constructor & Default constructor
// initialize data members, with default values
// accessable to const object by default
Point_2D(const double &arg_x = 0, const double &arg_y = 0);
// Copy constructor
// copy the data members from the given object
// accessable to const object by default
Point_2D(const Point_2D &arg_point);
// Destructor
~Point_2D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// Member functions
// we use lower case letter to indicate a member function
// also, we just define the function declaration
// and leave the definition to the end of the class
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set(const double &arg_x, const double &arg_y);
// get the x coordinate and y coordinate
// accessable to const object
double get_x() const;
double get_y() const;
// // compare two points
bool operator==(const Point_2D &arg_point) const;
bool operator!=(const Point_2D &arg_point) const;
bool operator<(const Point_2D &arg_point) const;
bool operator>(const Point_2D &arg_point) const;
bool operator<=(const Point_2D &arg_point) const;
bool operator>=(const Point_2D &arg_point) const;
// assign the point with another point
Point_2D &operator=(const Point_2D &arg_point);
// friend class
friend class Triangle_2D;
// friend function
// print the x and y coordinate in format (x, y)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os, const Point_2D &arg_point);
// read the coordinate of a point from the input, format: (x, y) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Point_2D &arg_point);
};
// Triangle_2D class declaration
class Triangle_2D
{
private:
// define three points of the Triangle_2D
// in array of Point_2D format
Point_2D m_point[3];
// check & correct the Triangle_2D points to counterclockwise order
void _check_points();
public:
// Constructor
Triangle_2D(const double &arg_x0 = 0.0, const double &arg_y0 = 0.0,
const double &arg_x1 = 0.0, const double &arg_y1 = 0.0,
const double &arg_x2 = 0.0, const double &arg_y2 = 0.0);
// Copy constructor
Triangle_2D(const Triangle_2D &arg_triangle);
// Destructor
~Triangle_2D()
{
// do nothing
}
// modify the three points of the Triangle_2D
void set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2);
void set_point1(const double &arg_x0, const double &arg_y0);
void set_point2(const double &arg_x1, const double &arg_y1);
void set_point3(const double &arg_x2, const double &arg_y2);
void set_x0(const double &arg_x0);
void set_y0(const double &arg_y0);
void set_x1(const double &arg_x1);
void set_y1(const double &arg_y1);
void set_x2(const double &arg_x2);
void set_y2(const double &arg_y2);
// get the three points of the Triangle_2D
double get_x0() const;
double get_y0() const;
double get_x1() const;
double get_y1() const;
double get_x2() const;
double get_y2() const;
// calculate the area of the Triangle_2D
double area();
// print the Triangle_2D
// format: ((x0, y0), (x1, y1), (x2, y2))
friend std::ostream &operator<<(std::ostream &arg_os, const Triangle_2D &arg_tri);
// read the coordinate of a point from the input,
// format: ((x0, y0), (x1, y1), (x2, y2)) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Triangle_2D &arg_tri);
};
// function definition
// check if the point is valid
void Point_2D::_check_validity()
{
// check if the x coordinate is valid
if (m_x < 0)
{
// if not, set it to 0
m_x = 0;
}
// check if the y coordinate is valid
if (m_y < 0)
{
// if not, set it to 0
m_y = 0;
}
}
// Constructor & Default constructor
// initialize data members, with default values
Point_2D::Point_2D(const double &arg_x, const double &arg_y)
// use `: var_name1(arg_var_name1), var_name2(arg_var_name2)`
// to initialize data members
: m_x(arg_x),
m_y(arg_y)
{
// check if the point is valid
_check_validity();
}
// Copy constructor
// copy the data members from the given object
Point_2D::Point_2D(const Point_2D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y)
{
// check if the point is valid
_check_validity();
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_2D::set_x(const double &arg_x)
{
m_x = arg_x;
// check if the point is valid
_check_validity();
}
void Point_2D::set_y(const double &arg_y)
{
m_y = arg_y;
// check if the point is valid
_check_validity();
}
void Point_2D::set(const double &arg_x, const double &arg_y)
{
m_x = arg_x;
m_y = arg_y;
// check if the point is valid
_check_validity();
}
// get the x coordinate and y coordinate
// accessable to const object
double Point_2D::get_x() const
{
return m_x;
}
double Point_2D::get_y() const
{
return m_y;
}
// // compare two points
bool Point_2D::operator==(const Point_2D &arg_point) const
{
// if the x and y coordinates are equal,
// return true
return (m_x == arg_point.m_x && m_y == arg_point.m_y);
}
bool Point_2D::operator!=(const Point_2D &arg_point) const
{
return !(*this == arg_point);
}
bool Point_2D::operator<(const Point_2D &arg_point) const
{
// if the x coordinate is smaller than the other point,
// return true
if (m_x < arg_point.m_x)
{
return true;
}
// if the x coordinate is equal to the other point,
// check if the y coordinate is smaller than the other point
else if (m_x == arg_point.m_x)
{
// if the y coordinate is smaller, return true
if (m_y < arg_point.m_y)
{
return true;
}
// if the y coordinate is equal to the other point,
// return false
else if (m_y == arg_point.m_y)
{
return false;
}
// if the y coordinate is larger, return false
else
{
return false;
}
}
// if the x coordinate is larger, return false
else
{
return false;
}
}
bool Point_2D::operator>(const Point_2D &arg_point) const
{
return !(*this < arg_point || *this == arg_point);
}
bool Point_2D::operator<=(const Point_2D &arg_point) const
{
return (*this < arg_point || *this == arg_point);
}
bool Point_2D::operator>=(const Point_2D &arg_point) const
{
return !(*this < arg_point);
}
// assign the point with another point
Point_2D &Point_2D::operator=(const Point_2D &arg_point)
{
// check if the point is valid
_check_validity();
// assign the x and y coordinate
m_x = arg_point.m_x;
m_y = arg_point.m_y;
// check if the point is valid
_check_validity();
return *this;
}
// print the point in the format (x, y)
std::ostream &operator<<(std::ostream &arg_os, const Point_2D &arg_point)
{
arg_os << "(" << arg_point.m_x << ", " << arg_point.m_y << ")";
return arg_os;
}
// read the coordinate of a point from the input, format: (x, y) and ignore space
std::istream &operator>>(std::istream &arg_is, Point_2D &arg_point)
{
string str_x, str_y, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ')'))
{
arg_point.m_x = stod(str_x);
arg_point.m_y = stod(str_y);
}
}
}
// check if the point is valid
arg_point._check_validity();
return arg_is;
}
// Triangle_2D class implementation
// check & correct the Triangle_2D points to counterclockwise order
void Triangle_2D::_check_points()
{
// sort the points in ascending order
for (int i = 0; i < 3; i++)
{
for (int j = i + 1; j < 3; j++)
{
if (m_point[i] > m_point[j])
{
// swap the points
Point_2D temp = m_point[i];
m_point[i] = m_point[j];
m_point[j] = temp;
}
}
}
// if the area is negative, swap the points
if (area() < 0.0)
{
Point_2D temp = m_point[0];
m_point[0] = m_point[1];
m_point[1] = temp;
}
}
// Constructor
Triangle_2D::Triangle_2D(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
: m_point{Point_2D(arg_x0, arg_y0),
Point_2D(arg_x1, arg_y1),
Point_2D(arg_x2, arg_y2)} // init the array with {}
{
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// Copy constructor
Triangle_2D::Triangle_2D(const Triangle_2D &arg_triangle)
: m_point{Point_2D(arg_triangle.m_point[0]),
Point_2D(arg_triangle.m_point[1]),
Point_2D(arg_triangle.m_point[2])} // init the array with {}
{
}
// set the three points of the Triangle_2D
void Triangle_2D::set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
{
m_point[0].set(arg_x0, arg_y0);
m_point[1].set(arg_x1, arg_y1);
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point1(const double &arg_x0, const double &arg_y0)
{
m_point[0].set(arg_x0, arg_y0);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point2(const double &arg_x1, const double &arg_y1)
{
m_point[1].set(arg_x1, arg_y1);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point3(const double &arg_x2, const double &arg_y2)
{
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x0(const double &arg_x0)
{
m_point[0].m_x = arg_x0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y0(const double &arg_y0)
{
m_point[0].m_y = arg_y0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x1(const double &arg_x1)
{
m_point[1].m_x = arg_x1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y1(const double &arg_y1)
{
m_point[1].m_y = arg_y1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x2(const double &arg_x2)
{
m_point[2].m_x = arg_x2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y2(const double &arg_y2)
{
m_point[2].m_y = arg_y2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// get the three points of the Triangle_2D
double Triangle_2D::get_x0() const
{
return m_point[0].m_x;
}
double Triangle_2D::get_y0() const
{
return m_point[0].m_y;
}
double Triangle_2D::get_x1() const
{
return m_point[1].m_x;
}
double Triangle_2D::get_y1() const
{
return m_point[1].m_y;
}
double Triangle_2D::get_x2() const
{
return m_point[2].m_x;
}
double Triangle_2D::get_y2() const
{
return m_point[2].m_y;
}
// calculate the area of the Triangle_2D
double Triangle_2D::area()
{
// calculate the area of the Triangle_2D
return (m_point[0].m_x * m_point[1].m_y +
m_point[1].m_x * m_point[2].m_y +
m_point[2].m_x * m_point[0].m_y -
m_point[0].m_x * m_point[2].m_y -
m_point[1].m_x * m_point[0].m_y -
m_point[2].m_x * m_point[1].m_y) /
2.0;
}
// print the Triangle_2D
// format: ((x0, y0), (x1, y1), (x2, y2))
std::ostream &operator<<(std::ostream &arg_os, const Triangle_2D &arg_tri)
{
arg_os << "(";
for (int i = 0; i < 3; i++)
{
arg_os << arg_tri.m_point[i];
if (i < 2)
arg_os << ", ";
}
arg_os << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: ((x0, y0), (x1, y1), (x2, y2)) and ignore space
std::istream &operator>>(std::istream &arg_is, Triangle_2D &arg_tri)
{
string temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
for (int i = 0; i < 3; i++)
{
arg_is >> arg_tri.m_point[i];
if (i < 2)
{
getline(arg_is, temp, ','); // ignore the ','
}
}
getline(arg_is, temp, ')'); // ignore the last ')'
}
// check & correct the Triangle_2D points to counterclockwise order
arg_tri._check_points();
return arg_is;
}
// main function
int main()
{
Triangle_2D t(1, 1, 2, 2, 0, 3);
cout << t << endl;
cout << "Area: " << t.area() << endl;
ofstream t_file("triangle.txt", ios::out | ios::trunc);
// reuse the `<<` operator to write the Triangle_2D to the file
t_file << t << endl;
t_file.close();
// read the Triangle_2D from the file
ifstream t_file_in("triangle.txt", ios::in);
Triangle_2D t_in;
t_file_in >> t_in;
cout << t_in << endl;
cout << "Area: " << t_in.area() << endl;
t_file_in.close();
return 0;
}
Example 2: Vector & Matrix in Binary File (class ver.)
#include <iostream>
#include <fstream>
#include <cmath>
using namespace std;
class Vector_3D; // forward declaration
class Point_3D // represents a point in 3D space
{
private:
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// record the z coordinate
double m_z;
public:
Point_3D(const double &arg_x = 0, const double &arg_y = 0,
const double &arg_z = 0);
Point_3D(const Point_3D &arg_point);
// Destructor
~Point_3D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// modify the x, y and z coordinate
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
void set(const double &arg_x, const double &arg_y, const double &arg_z);
// get the x, y and z coordinate
double get_x() const;
double get_y() const;
double get_z() const;
// calculate the distance between two points
// in form of a vector
Vector_3D operator-(const Point_3D &arg_point) const;
// friend class
friend class Vector_3D;
// print the x and y coordinate in format (x, y, z)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os, const Point_3D &arg_point);
// read the coordinate of a point from the input,
// format: (x, y, z) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Point_3D &arg_point);
};
// Vector_3D class declaration
class Vector_3D
{
private:
// define the three factor of the basis vectors
// on the x, y, z axes
double m_x, m_y, m_z;
public:
// Constructor
Vector_3D(const double &arg_x = 0.0, const double &arg_y = 0.0,
const double &arg_z = 0.0);
Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2);
// Copy constructor
Vector_3D(const Vector_3D &arg_vector);
// Destructor
~Vector_3D()
{
// do nothing
}
// set the three factor of the basis vectors
void set_vector(const double &arg_x, const double &arg_y,
const double &arg_z);
void set_vector(const Point_3D &arg_point1, const Point_3D &arg_point2);
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
// get the three factor of the basis vectors
double get_x() const;
double get_y() const;
double get_z() const;
// assign operator
Vector_3D &operator=(const Vector_3D &arg_vector);
// calculate the length of the Vector_3D
double length();
// calculate the dot product of two vectors
int dot(const Vector_3D &);
// calculate the cross product of two vectors
Vector_3D cross(const Vector_3D &);
// write the Vector_3D in binary format
void write_binary(std::ofstream &arg_ofs);
// read the Vector_3D in binary format
void read_binary(std::ifstream &arg_ifs);
// print the Vector_3D in format (x, y, z)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os,
const Vector_3D &arg_point);
// read the factors of a vector from the input,
// format: (x, y, z) and ignore space
friend std::istream &operator>>(std::istream &arg_is,
Vector_3D &arg_point);
};
// Point_3D class implementation
// Constructor & Default constructor
// initialize data members, with default values
Point_3D::Point_3D(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x),
m_y(arg_y),
m_z(arg_z)
{
}
// Copy constructor
// copy the data members from the given object
Point_3D::Point_3D(const Point_3D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y),
m_z(arg_point.m_z)
{
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_3D::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Point_3D::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Point_3D::set(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
// get the x coordinate and y coordinate
// accessable to const object
double Point_3D::get_x() const
{
return m_x;
}
double Point_3D::get_y() const
{
return m_y;
}
double Point_3D::get_z() const
{
return m_z;
}
// calculate the distance between two points
// in form of a vector
Vector_3D Point_3D::operator-(const Point_3D &arg_point) const
{
return Vector_3D(*this, arg_point);
}
// print the point in the format (x, y, z)
std::ostream &operator<<(std::ostream &arg_os, const Point_3D &arg_point)
{
arg_os << "(" << arg_point.m_x << ", " << arg_point.m_y
<< ", " << arg_point.m_z << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: (x, y, z) and ignore space
std::istream &operator>>(std::istream &arg_is, Point_3D &arg_point)
{
string str_x, str_y, str_z, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ','))
{
if (getline(arg_is, str_z, ')'))
{
arg_point.m_x = stod(str_x);
arg_point.m_y = stod(str_y);
arg_point.m_z = stod(str_z);
}
}
}
}
return arg_is;
}
// Vector_3D class implementation
// Constructor
Vector_3D::Vector_3D(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x), m_y(arg_y), m_z(arg_z)
{
}
Vector_3D::Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2)
: m_x(arg_point2.m_x - arg_point1.m_x),
m_y(arg_point2.m_y - arg_point1.m_y),
m_z(arg_point2.m_z - arg_point1.m_z)
{
}
// Copy constructor
Vector_3D::Vector_3D(const Vector_3D &arg_vector)
: m_x(arg_vector.m_x), m_y(arg_vector.m_y), m_z(arg_vector.m_z)
{
}
// set the three factor of the basis vectors
void Vector_3D::set_vector(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
void Vector_3D::set_vector(const Point_3D &arg_point1,
const Point_3D &arg_point2)
{
m_x = arg_point2.m_x - arg_point1.m_x;
m_y = arg_point2.m_y - arg_point1.m_y;
m_z = arg_point2.m_z - arg_point1.m_z;
}
void Vector_3D::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Vector_3D::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Vector_3D::set_z(const double &arg_z)
{
m_z = arg_z;
}
// get the three factor of the basis vectors
double Vector_3D::get_x() const
{
return m_x;
}
double Vector_3D::get_y() const
{
return m_y;
}
double Vector_3D::get_z() const
{
return m_z;
}
// assign operator
Vector_3D &Vector_3D::operator=(const Vector_3D &arg_vector)
{
m_x = arg_vector.m_x;
m_y = arg_vector.m_y;
m_z = arg_vector.m_z;
return *this;
}
// calculate the length of the Vector_3D
double Vector_3D::length()
{
// calculate the length of the Vector_3D
return sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
}
// calculate the dot product of two vectors
int Vector_3D::dot(const Vector_3D &arg_v)
{
// calculate the dot product of two vectors
return m_x * arg_v.m_x + m_y * arg_v.m_y + m_z * arg_v.m_z;
}
// calculate the cross product of two vectors
Vector_3D Vector_3D::cross(const Vector_3D &arg_v)
{
// calculate the cross product of two vectors
Vector_3D v;
v.m_x = m_y * arg_v.m_z - m_z * arg_v.m_y;
v.m_y = m_z * arg_v.m_x - m_x * arg_v.m_z;
v.m_z = m_x * arg_v.m_y - m_y * arg_v.m_x;
return v;
}
// write the vector to the file in binary format
void Vector_3D::write_binary(std::ofstream &arg_ofs)
{
arg_ofs.write((char *)&m_x, sizeof(double));
arg_ofs.write((char *)&m_y, sizeof(double));
arg_ofs.write((char *)&m_z, sizeof(double));
}
// read the vector from the file in binary format
void Vector_3D::read_binary(std::ifstream &arg_ifs)
{
arg_ifs.read((char *)&m_x, sizeof(double));
arg_ifs.read((char *)&m_y, sizeof(double));
arg_ifs.read((char *)&m_z, sizeof(double));
}
// print the point in the format (x, y, z)
std::ostream &operator<<(std::ostream &arg_os, const Vector_3D &arg_vector)
{
arg_os << "(" << arg_vector.m_x << ", " << arg_vector.m_y
<< ", " << arg_vector.m_z << ")";
return arg_os;
}
// read the factors of a vector from the input,
// format: (x, y, z) and ignore space
std::istream &operator>>(std::istream &arg_is, Vector_3D &arg_vector)
{
string str_x, str_y, str_z, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ','))
{
if (getline(arg_is, str_z, ')'))
{
arg_vector.m_x = stod(str_x);
arg_vector.m_y = stod(str_y);
arg_vector.m_z = stod(str_z);
}
}
}
}
return arg_is;
}
// main function
int main()
{
Vector_3D v1(1, 2, 3);
Vector_3D v2(4, 5, 6);
cout << "v1 = " << v1 << endl;
cout << "v2 = " << v2 << endl;
// save the vector to the file in binary format
ofstream ofs("vector.bin", ios::binary | ios::trunc);
v1.write_binary(ofs);
v2.write_binary(ofs);
ofs.close();
// read the vector from the file in binary format
ifstream ifs("vector.bin", ios::binary);
Vector_3D v3, v4;
v3.read_binary(ifs);
v4.read_binary(ifs);
cout << "v3 = " << v3 << endl;
cout << "v4 = " << v4 << endl;
// or read/write whole object
ofstream ofs2("vector_whole.bin", ios::binary | ios::trunc);
ofs2.write((char *)&v1, sizeof(Vector_3D));
ofs2.write((char *)&v2, sizeof(Vector_3D));
ofs2.close();
ifstream ifs2("vector_whole.bin", ios::binary);
Vector_3D v5, v6;
ifs2.read((char *)&v5, sizeof(Vector_3D));
ifs2.read((char *)&v6, sizeof(Vector_3D));
cout << "v5 = " << v5 << endl;
cout << "v6 = " << v6 << endl;
// NOTE: compaire "vector.bin" and "vector_whole.bin"
return 0;
}
Lab 14: File Export of Complex Number's Geometry
Lab 14-1: Simple Complex Number Geometry Transformation (Text File ver.) (75%)
- 輸入:
- 從檔案中讀取多個幾何形狀或幾何變換的複數資料。
- 請使用
int main(int argc, char *argv[])來開啟指定檔案 (Ref: One and the only: main function。 - 開啟檔案名稱會放在
argv[1]中。
- 請使用
- 幾何圖形
- 以
char格式讀取幾何圖形形狀,包含三角形 (t)、四邊形 (q)、多邊形 (p)、圓形 (c),一行讀取一個幾何圖形 - 以
unsinged int格式讀取幾何圖形的頂點數,一行讀取一個正整數- 三角形:3
- 四邊形:4
- 多邊形:大於 3 的正整數
- 圓形:2
- 以
double格式讀取組合幾何圖形的複數的實數及虛數部分,以空格分開,一行讀取一個複數 - 讀取幾何圖形形狀及頂點數後依據 2. 的頂點數接著讀取相對應的複數
- 三角形:連續讀取三個複數
- 四邊形:連續讀取四個複數
- 多邊形:連續讀取多個複數
- 圓形:連續讀取兩個複數
- 幾何變換
- 以
char格式讀取幾何變換字元,包含以0點旋轉 (r)、以0點縮放 (z)、平移 (m),一行讀取一個幾何變換 - 以
double格式讀取幾何變換的複數的實數及虛數部分,以空格分開,一行讀取一個複數- 以
0點旋轉:\(z * (cos(\theta) + sin(\theta)i), norm = 1\) - 以
0點縮放:\(z * (r + 0i)\) - 平移:\(z + (x + yi)\)
- 以
- 讀取幾何變換後須將所有的幾何圖形複數變換
- 從檔案中讀取多個幾何形狀或幾何變換的複數資料。
- 輸出:
- 將結果的幾何形狀及幾何變換的複數資料輸出至指令列及檔案中。
- 請使用
int main(int argc, char *argv[])來開啟指定檔案 (Ref: One and the only: main function。 - 開啟檔案名稱會放在
argv[2]中。
- 請使用
- 幾何圖形
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 格式請參考 Format 中的說明
- 頂點順序與讀取順序相同
- 複數的格式為
(-)<real result> (+|-) (<imag result>i)- 若虛數部分為 0 則僅顯示實數部分
- 若虛數部分小於 0 則中間的
+要改成-,並且虛數部分要顯示絕對值
- 虛數及實數部分皆以預設
double格式顯示
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 幾何變換
- 輸出變換後的所有幾何圖形複數
- 將結果的幾何形狀及幾何變換的複數資料輸出至指令列及檔案中。
- 檔名:
lab14-1_<學號>.cpp(e.g.lab14-1_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果
- 使用者不需要處理錯誤輸入
- 請基於 pseudo code 提供的
main及print_output_file進行修改來處理輸入與輸出 - 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Input Format
Geometry Objects
<geometry type>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<EOF>
Transformation
<geometry type 1>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<geometry type 2>⏎
n⏎
<real 1> <imag 1>⏎
<real 2> <imag 2>⏎
...
<real n> <imag n>⏎
<geometry transformation type>⏎
(-)<real trans> (+|-) (<imag trans>i)⏎
<EOF>
Output Format
Geometry Objects
<geometry type>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
Transformation
<geometry type 1>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
<geometry type 2>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
<geometry type 1>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
<geometry type 2>
n
(-)<real 1> (+|-) (<imag 1>i)
(-)<real 2> (+|-) (<imag 2>i)
...
(-)<real n> (+|-) (<imag n>i)
...
Example
Geometry Objects
Triangle
Input File: input_triangle.txt
t
3
1.0 2.0
3.0 4.0
5.0 0.0
Output File: output_triangle.txt
t
3
1 + 2i
3 + 4i
5
Terminal:
$ ./a.out input_triangle.txt output_triangle.txt
t
3
1 + 2i
3 + 4i
5
$
Quadrilateral
Input File: input_quadrilateral.txt
q
4
1.0 2.0
3.0 2.0
3.0 4.0
1.0 4.0
Output File: output_quadrilateral.txt
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
Terminal:
$ ./a.out input_quadrilateral.txt output_quadrilateral.txt
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
$
Circle
Input File: input_circle.txt
c
2
1.0 2.0
3.0 4.0
Output File: output_circle.txt
c
2
1 + 2i
3 + 4i
Terminal:
$ ./a.out input_circle.txt output_circle.txt
c
2
1 + 2i
3 + 4i
$
Polygon
Input File: input_polygon.txt
p
5
1.0 0.0
2.0 1.1
-3.0 -2.2
4.3 2.1
-1.2 3.4
Output File: output_polygon.txt
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
Terminal:
$ ./a.out input_polygon.txt output_polygon.txt
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
$
Multiple Objects
Input File: input_multiple_objects.txt
t
3
1.0 2.0
3.0 4.0
5.0 0.0
q
4
1.0 2.0
3.0 2.0
3.0 4.0
1.0 4.0
c
2
1.0 2.0
3.0 4.0
p
5
1.0 0.0
2.0 1.1
-3.0 -2.2
4.3 2.1
-1.2 3.4
Output File: output_multiple_objects.txt
t
3
1 + 2i
3 + 4i
5
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c
2
1 + 2i
3 + 4i
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
Terminal:
$ ./a.out input_multiple.txt output_multiple.txt
t
3
1 + 2i
3 + 4i
5
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c
2
1 + 2i
3 + 4i
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
$
Transformation
Scaling
Input File: input_scaling.txt
t
3
1.0 2.0
3.0 4.0
5.0 0.0
z
2.0 0.0
Output File: output_scaling.txt
t
3
1 + 2i
3 + 4i
5
t
3
2 + 4i
6 + 8i
10
Terminal:
$ ./a.out input_scaling.txt output_scaling.txt
t
3
1 + 2i
3 + 4i
5
t
3
2 + 4i
6 + 8i
10
$
Translation
Input File: input_translation.txt
q
4
1.0 2.0
3.0 2.0
3.0 4.0
1.0 4.0
m
3.0 -1.0
Output File: output_translation.txt
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
q
4
4 + 1i
6 + 1i
6 + 3i
4 + 3i
Terminal:
$ ./a.out input_translation.txt output_translation.txt
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
q
4
4 + 1i
6 + 1i
6 + 3i
4 + 3i
$
Rotation
Input File: input_rotation.txt
c
2
1.0 2.0
3.0 4.0
r
0.99990604980155 0.013707354604752
Output File: output_rotation.txt
c
2
1 + 2i
3 + 4i
c
2
0.972491 + 2.01352i
2.94489 + 4.04075i
Terminal:
$ ./a.out input_rotation.txt output_rotation.txt
c
2
1 + 2i
3 + 4i
c
2
0.972491 + 2.01352i
2.94489 + 4.04075i
$
Multiple Transformations
Input File: input_multiple_transformations.txt
p
5
1.0 0.0
2.0 1.1
-3.0 -2.2
4.3 2.1
-1.2 3.4
z
2.0 0.0
m
3.0 -1.0
r
0.99990604980155 0.013707354604752
Output File: output_multiple_transformations.txt
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
p
5
2
4 + 2.2i
-6 - 4.4i
8.6 + 4.2i
-2.4 + 6.8i
p
5
5 - 1i
7 + 1.2i
-3 - 5.4i
11.6 + 3.2i
0.6 + 5.8i
p
5
5.01324 - 0.931369i
6.98289 + 1.29584i
-2.9257 - 5.44061i
11.555 + 3.3587i
0.520441 + 5.80768i
Terminal:
$ ./a.out input_multiple_transformations.txt output_multiple_transformations.txt
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
p
5
2
4 + 2.2i
-6 - 4.4i
8.6 + 4.2i
-2.4 + 6.8i
p
5
5 - 1i
7 + 1.2i
-3 - 5.4i
11.6 + 3.2i
0.6 + 5.8i
p
5
5.01324 - 0.931369i
6.98289 + 1.29584i
-2.9257 - 5.44061i
11.555 + 3.3587i
0.520441 + 5.80768i
$
Multiple Transformations on Multiple Objects
Input File: input_mix.txt
t
3
1.0 2.0
3.0 4.0
5.0 0.0
q
4
1.0 2.0
3.0 2.0
3.0 4.0
1.0 4.0
c
2
1.0 2.0
3.0 4.0
p
5
1.0 0.0
2.0 1.1
-3.0 -2.2
4.3 2.1
-1.2 3.4
z
2.0 0.0
m
3.0 -1.0
r
0.99990604980155 0.013707354604752
Output File: output_mix.txt
t
3
1 + 2i
3 + 4i
5
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c
2
1 + 2i
3 + 4i
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
t
3
2 + 4i
6 + 8i
10
q
4
2 + 4i
6 + 4i
6 + 8i
2 + 8i
c
2
2 + 4i
6 + 8i
p
5
2
4 + 2.2i
-6 - 4.4i
8.6 + 4.2i
-2.4 + 6.8i
t
3
5 + 3i
9 + 7i
13 - 1i
q
4
5 + 3i
9 + 3i
9 + 7i
5 + 7i
c
2
5 + 3i
9 + 7i
p
5
5 - 1i
7 + 1.2i
-3 - 5.4i
11.6 + 3.2i
0.6 + 5.8i
t
3
4.95841 + 3.06825i
8.9032 + 7.12271i
13.0125 - 0.82171i
q
4
4.95841 + 3.06825i
8.95803 + 3.12308i
8.9032 + 7.12271i
4.90358 + 7.06788i
c
2
4.95841 + 3.06825i
8.9032 + 7.12271i
p
5
5.01324 - 0.931369i
6.98289 + 1.29584i
-2.9257 - 5.44061i
11.555 + 3.3587i
0.520441 + 5.80768i
Terminal:
$ ./a.out input_mix.txt output_mix.txt
t
3
1 + 2i
3 + 4i
5
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c
2
1 + 2i
3 + 4i
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
t
3
2 + 4i
6 + 8i
10
q
4
2 + 4i
6 + 4i
6 + 8i
2 + 8i
c
2
2 + 4i
6 + 8i
p
5
2
4 + 2.2i
-6 - 4.4i
8.6 + 4.2i
-2.4 + 6.8i
t
3
5 + 3i
9 + 7i
13 - 1i
q
4
5 + 3i
9 + 3i
9 + 7i
5 + 7i
c
2
5 + 3i
9 + 7i
p
5
5 - 1i
7 + 1.2i
-3 - 5.4i
11.6 + 3.2i
0.6 + 5.8i
t
3
4.95841 + 3.06825i
8.9032 + 7.12271i
13.0125 - 0.82171i
q
4
4.95841 + 3.06825i
8.95803 + 3.12308i
8.9032 + 7.12271i
4.90358 + 7.06788i
c
2
4.95841 + 3.06825i
8.9032 + 7.12271i
p
5
5.01324 - 0.931369i
6.98289 + 1.29584i
-2.9257 - 5.44061i
11.555 + 3.3587i
0.520441 + 5.80768i
$
Pseudo Code
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// length of the complex number
double length() const;
// angle of the complex number in radians
// use `atan2` to compute the angle by the formula `atan(imag/real)`
// and use `NAN` for 0/0 case
// `atan2` ref: https://en.cppreference.com/w/cpp/numeric/math/atan2
// `NAN` ref: https://en.cppreference.com/w/cpp/numeric/math/NAN
double angle() const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
// utility function to check if the transformation is valid
// hint: use `isnan` to check the angle is valid or not
// ref: https://en.cppreference.com/w/cpp/numeric/math/isnan
bool _check_transform(const Complex &arg_trans_c, const char &arg_op);
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
virtual void parse_geometry(ifstream &arg_ifs);
// apply transformation to the geometry
void transform_geometry(const Complex &arg_trans_c, const char &arg_op);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
void print_output_file(int argc, char *argv[])
{
ifstream ans_ifs(argv[2]);
if (!ans_ifs)
{
cout << "Error: Cannot open output file" << endl;
exit(1);
}
string ans_line;
while (getline(ans_ifs, ans_line))
{
cout << ans_line << endl;
}
ans_ifs.close();
}
int main(int argc, char *argv[])
{
string input, temp;
vector<Geometry_Comp *> geo_ptr_array;
Geometry_Comp *geo_ptr;
Complex trans_c;
char trans_op;
// open & check input file
// open & check output file
while (getline(infile, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
case 'r':
case 'z':
case 'm':
getline(infile, temp);
break;
default:
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
if (input[0] == 't' || input[0] == 'q' || input[0] == 'p' || input[0] == 'c')
{
// parse the cin to the geometry
geo_ptr->parse_geometry(infile);
// print the geometry
geo_ptr->print_geometry(outfile);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else if (input[0] == 'r' || input[0] == 'z' || input[0] == 'm')
{
stringstream ss(temp);
ss >> trans_c;
// transform the geometry using operator and complex
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->transform_geometry(trans_c, input[0]);
// print transformed geometry
geo_ptr_array[i]->print_geometry(outfile);
}
}
else
{
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
}
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
// close input and output file
print_output_file(argc, argv);
return 0;
}
Reference Code:
TA
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// length of the complex number
double length() const;
// angle of the complex number in radians
// use `atan2` to compute the angle by the formula `atan(imag/real)`
// and use `NAN` for 0/0 case
// `atan2` ref: https://en.cppreference.com/w/cpp/numeric/math/atan2
// `NAN` ref: https://en.cppreference.com/w/cpp/numeric/math/NAN
double angle() const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
// utility function to check if the transformation is valid
// hint: use `isnan` to check the angle is valid or not
// ref: https://en.cppreference.com/w/cpp/numeric/math/isnan
bool _check_transform(const Complex &arg_trans_c, const char &arg_op);
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
virtual void parse_geometry(ifstream &arg_ifs);
// apply transformation to the geometry
void transform_geometry(const Complex &arg_trans_c, const char &arg_op);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
void print_output_file(int argc, char *argv[])
{
ifstream ans_ifs(argv[2]);
if (!ans_ifs)
{
cout << "Error: Cannot open output file" << endl;
exit(1);
}
string ans_line;
while (getline(ans_ifs, ans_line))
{
cout << ans_line << endl;
}
ans_ifs.close();
}
// Complex class implementation
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
// Copy constructor
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
// assignment operator
Complex &Complex::operator=(const Complex &arg_c)
{
if (this == &arg_c) // self-assignment
return *this;
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
// add assignment operator
Complex &Complex::operator+=(const Complex &arg_c)
{
m_real += arg_c.m_real;
m_imag += arg_c.m_imag;
return *this;
}
// multiply assignment operator
Complex &Complex::operator*=(const Complex &arg_c)
{
double real = m_real * arg_c.m_real - m_imag * arg_c.m_imag;
double imag = m_real * arg_c.m_imag + m_imag * arg_c.m_real;
m_real = real;
m_imag = imag;
return *this;
}
// length of the complex number
double Complex::length() const
{
return sqrt(m_real * m_real + m_imag * m_imag);
}
// angle of the complex number in radians
double Complex::angle() const
{
if (m_real == 0 && m_imag == 0)
{
return NAN;
}
return atan2(m_imag, m_real);
}
// cout `<<` operator for print complex number
// note: be careful about the format of output
ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag > 0)
{
arg_os << arg_c.m_real << " + " << arg_c.m_imag << "i";
}
else if (arg_c.m_imag < 0)
{
arg_os << arg_c.m_real << " - " << -arg_c.m_imag << "i";
}
else
{
arg_os << arg_c.m_real;
}
return arg_os;
}
// cin `>>` operator for input complex number
// note: be careful about the format of input
istream &operator>>(istream &arg_is, Complex &arg_c)
{
double input_real, input_imag;
arg_is >> input_real;
if (arg_is.fail())
{
error_and_exit();
}
arg_is >> input_imag;
if (arg_is.fail() || !arg_is.eof())
{
error_and_exit();
}
arg_c.m_real = input_real;
arg_c.m_imag = input_imag;
return arg_is;
}
// Geometry_Comp class implementation
// check if the transformation is valid
bool Geometry_Comp::_check_transform(const Complex &arg_c, const char &arg_op)
{
// check if the operation is valid
if (arg_op == 'r' && (arg_c.length() != 1 || isnan(arg_c.angle())))
{
return false;
}
else if (arg_op == 'z' && (arg_c.m_real == 0 || arg_c.m_imag != 0))
{
return false;
}
else
{
return true;
}
}
// Constructor, initializes the array
Geometry_Comp::Geometry_Comp(const unsigned int &arg_num_of_vertex)
: m_comp_array(arg_num_of_vertex)
{
}
// Copy constructor
Geometry_Comp::Geometry_Comp(const Geometry_Comp &arg_gc)
: m_comp_array(arg_gc.m_comp_array)
{
}
// assignment operator
Geometry_Comp &Geometry_Comp::operator=(const Geometry_Comp &arg_gc)
{
if (this == &arg_gc) // self-assignment
return *this;
m_comp_array = arg_gc.m_comp_array;
return *this;
}
// print the geometry
void Geometry_Comp::print_geometry(ofstream &arg_ofs)
{
cout << "not implemented" << endl;
}
// parse the cin to the geometry
void Geometry_Comp::parse_geometry(ifstream &arg_ifs)
{
cout << "not implemented" << endl;
}
// apply transformation to the geometry
void Geometry_Comp::transform_geometry(const Complex &arg_c, const char &arg_op)
{
if (!(_check_transform(arg_c, arg_op)))
{
error_and_exit();
}
if (arg_op == 'm')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] += arg_c;
}
}
else if (arg_op == 'r' || arg_op == 'z')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] *= arg_c;
}
}
}
// set the geometry
void Geometry_Comp::set_geometry(const vector<Complex> &arg_comp_array)
{
m_comp_array = arg_comp_array;
}
// get the geometry array
vector<Complex> Geometry_Comp::get_geometry_array()
{
return m_comp_array;
}
// Triangle_Comp class implementation
// Constructor, initializes the array
Triangle_Comp::Triangle_Comp()
: Geometry_Comp(triangle_num_of_vertex)
{
}
// Copy constructor
Triangle_Comp::Triangle_Comp(const Triangle_Comp &arg_tc)
: Geometry_Comp(arg_tc)
{
}
// assignment operator
Triangle_Comp &Triangle_Comp::operator=(const Triangle_Comp &arg_tc)
{
if (this == &arg_tc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_tc);
return *this;
}
// print the geometry
void Triangle_Comp::print_geometry(ofstream &arg_ofs)
{
arg_ofs << "t" << endl;
arg_ofs << m_comp_array.size() << endl;
for (int i = 0; i < triangle_num_of_vertex; i++)
{
arg_ofs << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Triangle_Comp::parse_geometry(ifstream &arg_ifs)
{
string temp;
getline(arg_ifs, temp); // get the vertex number
stringstream ss(temp);
unsigned int vertex_num;
ss >> vertex_num;
if (vertex_num != triangle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_ifs, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Quadrilateral_Comp class implementation
// Constructor, initializes the array
Quadrilateral_Comp::Quadrilateral_Comp()
: Geometry_Comp(quadrilateral_num_of_vertex)
{
}
// Copy constructor
Quadrilateral_Comp::Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc)
: Geometry_Comp(arg_qc)
{
}
// assignment operator
Quadrilateral_Comp &Quadrilateral_Comp::operator=(const Quadrilateral_Comp &arg_qc)
{
if (this == &arg_qc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_qc);
return *this;
}
// print the geometry
void Quadrilateral_Comp::print_geometry(ofstream &arg_ofs)
{
arg_ofs << "q" << endl;
arg_ofs << m_comp_array.size() << endl;
for (int i = 0; i < quadrilateral_num_of_vertex; i++)
{
arg_ofs << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Quadrilateral_Comp::parse_geometry(ifstream &arg_ifs)
{
string temp;
getline(arg_ifs, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != quadrilateral_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_ifs, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Polygon_Comp class implementation
// Constructor, initializes the array
Polygon_Comp::Polygon_Comp()
: Geometry_Comp()
{
}
// Copy constructor
Polygon_Comp::Polygon_Comp(const Polygon_Comp &arg_pc)
: Geometry_Comp(arg_pc)
{
}
// assignment operator
Polygon_Comp &Polygon_Comp::operator=(const Polygon_Comp &arg_pc)
{
if (this == &arg_pc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_pc);
return *this;
}
// print the geometry
void Polygon_Comp::print_geometry(ofstream &arg_ofs)
{
arg_ofs << "p" << endl;
arg_ofs << m_comp_array.size() << endl;
for (int i = 0; i < m_comp_array.size(); i++)
{
arg_ofs << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Polygon_Comp::parse_geometry(ifstream &arg_ifs)
{
string temp;
getline(arg_ifs, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num < triangle_num_of_vertex)
{
error_and_exit();
}
m_comp_array.resize(vertex_num);
for (int i = 0; i < vertex_num; i++)
{
getline(arg_ifs, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Circle_Comp class implementation
// Constructor, initializes the array
Circle_Comp::Circle_Comp()
: Geometry_Comp(circle_num_of_vertex)
{
}
// Copy constructor
Circle_Comp::Circle_Comp(const Circle_Comp &arg_cc)
: Geometry_Comp(arg_cc)
{
}
// assignment operator
Circle_Comp &Circle_Comp::operator=(const Circle_Comp &arg_cc)
{
if (this == &arg_cc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_cc);
return *this;
}
// print the geometry
void Circle_Comp::print_geometry(ofstream &arg_ofs)
{
arg_ofs << "c" << endl;
arg_ofs << m_comp_array.size() << endl;
for (int i = 0; i < circle_num_of_vertex; i++)
{
arg_ofs << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Circle_Comp::parse_geometry(ifstream &arg_ifs)
{
string temp;
getline(arg_ifs, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != circle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_ifs, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
int main(int argc, char *argv[])
{
string input, temp;
vector<Geometry_Comp *> geo_ptr_array;
Geometry_Comp *geo_ptr;
Complex trans_c;
char trans_op;
string input_file_path(argv[1]);
string output_file_path(argv[2]);
ifstream infile(input_file_path, ios::in);
if (!infile)
{
cout << "Input file cannot open." << endl;
return -1;
}
ofstream outfile(output_file_path, ios::out | ios::trunc);
if (!outfile)
{
cout << "Output file cannot open." << endl;
return -1;
}
while (getline(infile, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
case 'r':
case 'z':
case 'm':
getline(infile, temp);
break;
default:
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
if (input[0] == 't' || input[0] == 'q' || input[0] == 'p' || input[0] == 'c')
{
// parse the cin to the geometry
geo_ptr->parse_geometry(infile);
// print the geometry
geo_ptr->print_geometry(outfile);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else if (input[0] == 'r' || input[0] == 'z' || input[0] == 'm')
{
stringstream ss(temp);
ss >> trans_c;
// transform the geometry using operator and complex
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->transform_geometry(trans_c, input[0]);
// print transformed geometry
geo_ptr_array[i]->print_geometry(outfile);
}
}
else
{
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
}
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
infile.close();
outfile.close();
print_output_file(argc, argv);
return 0;
}
Lab 14-2: Simple Complex Number Geometry Transformation (Binary File ver.) (25%)
- 輸入:
- 從檔案中讀取多個幾何形狀或幾何變換的複數資料。
- 請使用
int main(int argc, char *argv[])來開啟指定檔案 (Ref: One and the only: main function。 - 開啟檔案名稱會放在
argv[1]中。
- 請使用
- 幾何圖形
- 以
char格式讀取幾何圖形形狀,包含三角形 (t)、四邊形 (q)、多邊形 (p)、圓形 (c),sizeof(char)byte 讀取一個幾何圖形 - 以
unsinged int格式讀取幾何圖形的頂點數,sizeof(unsigned)byte 讀取一個正整數- 三角形:3
- 四邊形:4
- 多邊形:大於 3 的正整數
- 圓形:2
- 以
double格式讀取組合幾何圖形的複數的實數及虛數部分,sizeof(double)byte 讀取一個實數或虛數部分 - 讀取幾何圖形形狀及頂點數後依據 2. 的頂點數接著讀取相對應的複數
- 三角形:連續讀取三個複數
- 四邊形:連續讀取四個複數
- 多邊形:連續讀取多個複數
- 圓形:連續讀取兩個複數
- 幾何變換
- 以
char格式讀取幾何變換字元,包含以0點旋轉 (r)、以0點縮放 (z)、平移 (m),sizeof(char)byte 讀取一個幾何變換 - 以
double格式讀取幾何變換的複數的實數及虛數部分,sizeof(double)byte 讀取一個實數或虛數部分- 以
0點旋轉:\(z * (cos(\theta) + sin(\theta)i), norm = 1\) - 以
0點縮放:\(z * (r + 0i)\) - 平移:\(z + (x + yi)\)
- 以
- 讀取幾何變換後須將所有的幾何圖形複數變換
- 從檔案中讀取多個幾何形狀或幾何變換的複數資料。
- 輸出:
- 將結果的幾何形狀及幾何變換的複數資料輸出至指令列及檔案中。
- 請使用
int main(int argc, char *argv[])來開啟指定檔案 (Ref: One and the only: main function。 - 開啟檔案名稱會放在
argv[2]中。
- 請使用
- 幾何圖形
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 格式請參考 Format 中的說明
- 頂點順序與讀取順序相同
- 複數的格式為
<real part in binary><imaginary part in binary>
- 顯示紀錄幾何圖形的形狀、頂點個數及其複數
- 幾何變換
- 輸出變換後的所有幾何圖形複數
- 將結果的幾何形狀及幾何變換的複數資料輸出至指令列及檔案中。
- 檔名:
lab14-2_<學號>.cpp(e.g.lab14-2_106062802.cpp)
注意事項:
- 程式不會輸出任何使用者提示,只會輸出程式結果
- 使用者不需要處理錯誤輸入
- 請基於 pseudo code 提供的
main及print_output_file進行修改來處理輸入與輸出 - 程式需要於 10 秒內完成,所有的測資皆會保證於 10 秒內完成
Input Format
Geometry Objects
<geometry type><n><real 1><imag 1><real 2><imag 2>...<real n> <imag n><EOF>
Transformation
<geometry type 1><n><real 1> <imag 1><real 2> <imag 2>...<real n> <imag n><geometry type 2><n><real 1> <imag 1><real 2> <imag 2>...<real n><imag n><geometry transformation type><real trans> <imag trans><EOF>
Output Format
Geometry Objects
<geometry type1><n><real 1><imag 1><real 2><imag 2>...<real n> <imag n><EOF>
Transformation
<geometry type1><n><real 1><imag 1><real 2><imag 2>...<real n> <imag n><geometry type1><n><real 1><imag 1><real 2><imag 2>...<real n><imag n><EOF>
Example
Note: 有 # 前置的行為註解,僅方便顯示,不會在 .bin 檔案內。
Geometry Objects
Triangle
Input File: input_triangle.bin
# t
# 3
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 5.000000000000000 0.000000000000000
# Hex dump
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00
Output File: output_triangle.bin
# t
# 3
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 5.000000000000000 0.000000000000000
# Hex dump
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00
Terminal:
$ ./a.out input_triangle.bin output_triangle.bin
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00
$
Quadrilateral
Input File: input_quadrilateral.bin
# q
# 4
# 1.000000000000000 2.000000000000000
# 3.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 1.000000000000000 4.000000000000000
# Hex dump
71 04 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 10 40
Output File: output_quadrilateral.bin
# q
# 4
# 1.000000000000000 2.000000000000000
# 3.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 1.000000000000000 4.000000000000000
# Hex dump
71 04 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 10 40
Terminal:
$ ./a.out input_quadrilateral.bin output_quadrilateral.bin
71 04 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 10 40
$
Circle
Input File: input_circle.bin
# c
# 2
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# Hex dump
63 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40
Output File: output_circle.bin
# c
# 2
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# Hex dump
63 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40
Terminal:
$ ./a.out input_circle.bin output_circle.bin
63 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40
$
Polygon
Input File: input_polygon.bin
# p
# 5
# 1.000000000000000 0.000000000000000
# 2.000000000000000 1.100000000000000
# -3.000000000000000 -2.200000000000000
# 4.300000000000000 2.100000000000000
# -1.200000000000000 3.400000000000000
# Hex dump
70 05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99
99 99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99
99 99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc
cc cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33
33 33 33 0b 40
Output File: output_polygon.bin
# p
# 5
# 1.000000000000000 0.000000000000000
# 2.000000000000000 1.100000000000000
# -3.000000000000000 -2.200000000000000
# 4.300000000000000 2.100000000000000
# -1.200000000000000 3.400000000000000
# Hex dump
70 05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99
99 99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99
99 99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc
cc cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33
33 33 33 0b 40
Terminal:
$ ./a.out input_polygon.bin output_polygon.bin
70 05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99
99 99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99
99 99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc
cc cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33
33 33 33 0b 40
$
Multiple Objects
Input File: input_multiple_objects.bin
# t
# 3
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 5.000000000000000 0.000000000000000
# q
# 4
# 1.000000000000000 2.000000000000000
# 3.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 1.000000000000000 4.000000000000000
# c
# 2
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# p
# 5
# 1.000000000000000 0.000000000000000
# 2.000000000000000 1.100000000000000
# -3.000000000000000 -2.200000000000000
# 4.300000000000000 2.100000000000000
# -1.200000000000000 3.400000000000000
# Hex dump
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00 71 04 00 00 00 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 10 40 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 10 40 63 02 00 00 00 00
00 00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00
00 00 00 00 00 08 40 00 00 00 00 00 00 10 40 70
05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99
99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99
99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc
cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33
33 33 0b 40
Output File: output_multiple_objects.bin
# t
# 3
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 5.000000000000000 0.000000000000000
# q
# 4
# 1.000000000000000 2.000000000000000
# 3.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 1.000000000000000 4.000000000000000
# c
# 2
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# p
# 5
# 1.000000000000000 0.000000000000000
# 2.000000000000000 1.100000000000000
# -3.000000000000000 -2.200000000000000
# 4.300000000000000 2.100000000000000
# -1.200000000000000 3.400000000000000
# Hex dump
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00 71 04 00 00 00 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 10 40 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 10 40 63 02 00 00 00 00
00 00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00
00 00 00 00 00 08 40 00 00 00 00 00 00 10 40 70
05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99
99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99
99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc
cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33
33 33 0b 40
Terminal:
$ ./a.out input_multiple.bin output_multiple.bin
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00 71 04 00 00 00 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 10 40 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 10 40 63 02 00 00 00 00
00 00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00
00 00 00 00 00 08 40 00 00 00 00 00 00 10 40 70
05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99
99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99
99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc
cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33
33 33 0b 40
$
Transformation
Scaling
Input File: input_scaling.bin
# t
# 3
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 5.000000000000000 0.000000000000000
# z
# 2.000000000000000 0.000000000000000
# Hex dump
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00 7a 00 00 00 00 00 00 00 40 00 00
00 00 00 00 00 00
Output File: output_scaling.bin
# t
# 3
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 5.000000000000000 0.000000000000000
# t
# 3
# 2.000000000000000 4.000000000000000
# 6.000000000000000 8.000000000000000
# 10.000000000000000 0.000000000000000
# Hex dump
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00 74 03 00 00 00 00 00 00 00 00 00
00 40 00 00 00 00 00 00 10 40 00 00 00 00 00 00
18 40 00 00 00 00 00 00 20 40 00 00 00 00 00 00
24 40 00 00 00 00 00 00 00 00
Terminal:
$ ./a.out input_scaling.bin output_scaling.bin
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00 74 03 00 00 00 00 00 00 00 00 00
00 40 00 00 00 00 00 00 10 40 00 00 00 00 00 00
18 40 00 00 00 00 00 00 20 40 00 00 00 00 00 00
24 40 00 00 00 00 00 00 00 00
$
Translation
Input File: input_translation.bin
# q
# 4
# 1.000000000000000 2.000000000000000
# 3.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 1.000000000000000 4.000000000000000
# m
# 3.000000000000000 -1.000000000000000
# Hex dump
71 04 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 10 40 6d 00 00 00 00 00 00 08 40 00 00
00 00 00 00 f0 bf
Output File: output_translation.bin
# q
# 4
# 1.000000000000000 2.000000000000000
# 3.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 1.000000000000000 4.000000000000000
# q
# 4
# 4.000000000000000 1.000000000000000
# 6.000000000000000 1.000000000000000
# 6.000000000000000 3.000000000000000
# 4.000000000000000 3.000000000000000
# Hex dump
71 04 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 10 40 71 04 00 00 00 00 00 00 00 00 00
10 40 00 00 00 00 00 00 f0 3f 00 00 00 00 00 00
18 40 00 00 00 00 00 00 f0 3f 00 00 00 00 00 00
18 40 00 00 00 00 00 00 08 40 00 00 00 00 00 00
10 40 00 00 00 00 00 00 08 40
Terminal:
$ ./a.out input_translation.bin output_translation.bin
71 04 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 10 40 71 04 00 00 00 00 00 00 00 00 00
10 40 00 00 00 00 00 00 f0 3f 00 00 00 00 00 00
18 40 00 00 00 00 00 00 f0 3f 00 00 00 00 00 00
18 40 00 00 00 00 00 00 08 40 00 00 00 00 00 00
10 40 00 00 00 00 00 00 08 40
$
Rotation
Input File: input_rotation.bin
# c
# 2
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# r
# 0.999906049801550 0.013707354604752
# Hex dump
63 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 72 ea 0b df f8 3a ff ef 3f 2e ca
ef fd 99 12 8c 3f
Output File: output_rotation.bin
# c
# 2
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# c
# 2
# 0.972491340592046 2.013519454207852
# 2.944888730985642 4.040746263020456
# Hex dump
63 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 63 02 00 00 00 99 8d ef 28 a6 1e
ef 3f bf 75 6d 16 b0 1b 00 40 c7 89 af d2 21 8f
07 40 a4 6d 6c 63 b9 29 10 40
Terminal:
$ ./a.out input_rotation.bin output_rotation.bin
63 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 63 02 00 00 00 99 8d ef 28 a6 1e
ef 3f bf 75 6d 16 b0 1b 00 40 c7 89 af d2 21 8f
07 40 a4 6d 6c 63 b9 29 10 40
$
Multiple Transformations
Input File: input_multiple_transformations.bin
# p
# 5
# 1.000000000000000 0.000000000000000
# 2.000000000000000 1.100000000000000
# -3.000000000000000 -2.200000000000000
# 4.300000000000000 2.100000000000000
# -1.200000000000000 3.400000000000000
# z
# 2.000000000000000 0.000000000000000
# m
# 3.000000000000000 -1.000000000000000
# r
# 0.999906049801550 0.013707354604752
# Hex dump
70 05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99
99 99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99
99 99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc
cc cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33
33 33 33 0b 40 7a 00 00 00 00 00 00 00 40 00 00
00 00 00 00 00 00 6d 00 00 00 00 00 00 08 40 00
00 00 00 00 00 f0 bf 72 ea 0b df f8 3a ff ef 3f
2e ca ef fd 99 12 8c 3f
Output File: output_multiple_transformations.bin
# p
# 5
# 1.000000000000000 0.000000000000000
# 2.000000000000000 1.100000000000000
# -3.000000000000000 -2.200000000000000
# 4.300000000000000 2.100000000000000
# -1.200000000000000 3.400000000000000
# p
# 5
# 2.000000000000000 0.000000000000000
# 4.000000000000000 2.200000000000000
# -6.000000000000000 -4.400000000000000
# 8.600000000000000 4.200000000000000
# -2.400000000000000 6.800000000000000
# p
# 5
# 5.000000000000000 -1.000000000000000
# 7.000000000000000 1.200000000000000
# -3.000000000000000 -5.400000000000000
# 11.600000000000000 3.200000000000000
# 0.600000000000000 5.800000000000000
# p
# 5
# 5.013237603612501 -0.931369276777790
# 6.982893523085147 1.295838741995124
# -2.925698434538989 -5.440614732742626
# 11.555046642962772 3.358704672780083
# 0.520440973173368 5.807679501611840
# Hex dump
70 05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99
99 99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99
99 99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc
cc cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33
33 33 33 0b 40 70 05 00 00 00 00 00 00 00 00 00
00 40 00 00 00 00 00 00 00 00 00 00 00 00 00 00
10 40 9a 99 99 99 99 99 01 40 00 00 00 00 00 00
18 c0 9a 99 99 99 99 99 11 c0 33 33 33 33 33 33
21 40 cd cc cc cc cc cc 10 40 33 33 33 33 33 33
03 c0 33 33 33 33 33 33 1b 40 70 05 00 00 00 00
00 00 00 00 00 14 40 00 00 00 00 00 00 f0 bf 00
00 00 00 00 00 1c 40 34 33 33 33 33 33 f3 3f 00
00 00 00 00 00 08 c0 9a 99 99 99 99 99 15 c0 33
33 33 33 33 33 27 40 9a 99 99 99 99 99 09 40 34
33 33 33 33 33 e3 3f 33 33 33 33 33 33 17 40 70
05 00 00 00 57 5f 8a 28 8e 0d 14 40 1e 50 08 f1
c6 cd ed bf 5a 67 c4 a3 7b ee 1b 40 36 24 9c 67
c1 bb f4 3f 46 6d b2 94 d4 67 07 c0 ba 0f 2d 82
30 c3 15 c0 34 8f d6 12 2f 1c 27 40 4b 1a 34 8e
a0 de 0a 40 a1 e5 e8 d3 73 a7 e0 3f 2c 4a d4 55
10 3b 17 40
Terminal:
$ ./a.out input_multiple_transformations.bin output_multiple_transformations.bin
70 05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99
99 99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99
99 99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc
cc cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33
33 33 33 0b 40 70 05 00 00 00 00 00 00 00 00 00
00 40 00 00 00 00 00 00 00 00 00 00 00 00 00 00
10 40 9a 99 99 99 99 99 01 40 00 00 00 00 00 00
18 c0 9a 99 99 99 99 99 11 c0 33 33 33 33 33 33
21 40 cd cc cc cc cc cc 10 40 33 33 33 33 33 33
03 c0 33 33 33 33 33 33 1b 40 70 05 00 00 00 00
00 00 00 00 00 14 40 00 00 00 00 00 00 f0 bf 00
00 00 00 00 00 1c 40 34 33 33 33 33 33 f3 3f 00
00 00 00 00 00 08 c0 9a 99 99 99 99 99 15 c0 33
33 33 33 33 33 27 40 9a 99 99 99 99 99 09 40 34
33 33 33 33 33 e3 3f 33 33 33 33 33 33 17 40 70
05 00 00 00 57 5f 8a 28 8e 0d 14 40 1e 50 08 f1
c6 cd ed bf 5a 67 c4 a3 7b ee 1b 40 36 24 9c 67
c1 bb f4 3f 46 6d b2 94 d4 67 07 c0 ba 0f 2d 82
30 c3 15 c0 34 8f d6 12 2f 1c 27 40 4b 1a 34 8e
a0 de 0a 40 a1 e5 e8 d3 73 a7 e0 3f 2c 4a d4 55
10 3b 17 40
$
Multiple Transformations on Multiple Objects
Input File: input_mix.bin
# t
# 3
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 5.000000000000000 0.000000000000000
# q
# 4
# 1.000000000000000 2.000000000000000
# 3.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 1.000000000000000 4.000000000000000
# c
# 2
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# p
# 5
# 1.000000000000000 0.000000000000000
# 2.000000000000000 1.100000000000000
# -3.000000000000000 -2.200000000000000
# 4.300000000000000 2.100000000000000
# -1.200000000000000 3.400000000000000
# z
# 2.000000000000000 0.000000000000000
# m
# 3.000000000000000 -1.000000000000000
# r
# 0.999906049801550 0.013707354604752
# Hex dump
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00 71 04 00 00 00 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 10 40 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 10 40 63 02 00 00 00 00
00 00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00
00 00 00 00 00 08 40 00 00 00 00 00 00 10 40 70
05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99
99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99
99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc
cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33
33 33 0b 40 7a 00 00 00 00 00 00 00 40 00 00 00
00 00 00 00 00 6d 00 00 00 00 00 00 08 40 00 00
00 00 00 00 f0 bf 72 ea 0b df f8 3a ff ef 3f 2e
ca ef fd 99 12 8c 3f
Output File: output_mix.bin
# t
# 3
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 5.000000000000000 0.000000000000000
# q
# 4
# 1.000000000000000 2.000000000000000
# 3.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# 1.000000000000000 4.000000000000000
# c
# 2
# 1.000000000000000 2.000000000000000
# 3.000000000000000 4.000000000000000
# p
# 5
# 1.000000000000000 0.000000000000000
# 2.000000000000000 1.100000000000000
# -3.000000000000000 -2.200000000000000
# 4.300000000000000 2.100000000000000
# -1.200000000000000 3.400000000000000
# t
# 3
# 2.000000000000000 4.000000000000000
# 6.000000000000000 8.000000000000000
# 10.000000000000000 0.000000000000000
# q
# 4
# 2.000000000000000 4.000000000000000
# 6.000000000000000 4.000000000000000
# 6.000000000000000 8.000000000000000
# 2.000000000000000 8.000000000000000
# c
# 2
# 2.000000000000000 4.000000000000000
# 6.000000000000000 8.000000000000000
# p
# 5
# 2.000000000000000 0.000000000000000
# 4.000000000000000 2.200000000000000
# -6.000000000000000 -4.400000000000000
# 8.600000000000000 4.200000000000000
# -2.400000000000000 6.800000000000000
# t
# 3
# 5.000000000000000 3.000000000000000
# 9.000000000000000 7.000000000000000
# 13.000000000000000 -1.000000000000000
# q
# 4
# 5.000000000000000 3.000000000000000
# 9.000000000000000 3.000000000000000
# 9.000000000000000 7.000000000000000
# 5.000000000000000 7.000000000000000
# c
# 2
# 5.000000000000000 3.000000000000000
# 9.000000000000000 7.000000000000000
# p
# 5
# 5.000000000000000 -1.000000000000000
# 7.000000000000000 1.200000000000000
# -3.000000000000000 -5.400000000000000
# 11.600000000000000 3.200000000000000
# 0.600000000000000 5.800000000000000
# t
# 3
# 4.958408185193494 3.068254922428410
# 8.903202965980686 7.122708540053618
# 13.012486002024902 -0.821710439939774
# q
# 4
# 4.958408185193494 3.068254922428410
# 8.958032384399694 3.123084340847418
# 8.903202965980686 7.122708540053618
# 4.903578766774485 7.067879121634610
# c
# 2
# 4.958408185193494 3.068254922428410
# 8.903202965980686 7.122708540053618
# p
# 5
# 5.013237603612501 -0.931369276777790
# 6.982893523085147 1.295838741995124
# -2.925698434538989 -5.440614732742626
# 11.555046642962772 3.358704672780083
# 0.520440973173368 5.807679501611840
# Hex dump
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00 71 04 00 00 00 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 10 40 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 10 40 63 02 00 00 00 00
00 00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00
00 00 00 00 00 08 40 00 00 00 00 00 00 10 40 70
05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99
99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99
99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc
cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33
33 33 0b 40 74 03 00 00 00 00 00 00 00 00 00 00
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 18
40 00 00 00 00 00 00 20 40 00 00 00 00 00 00 24
40 00 00 00 00 00 00 00 00 71 04 00 00 00 00 00
00 00 00 00 00 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 18 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 18 40 00 00 00 00 00 00 20 40 00 00
00 00 00 00 00 40 00 00 00 00 00 00 20 40 63 02
00 00 00 00 00 00 00 00 00 00 40 00 00 00 00 00
00 10 40 00 00 00 00 00 00 18 40 00 00 00 00 00
00 20 40 70 05 00 00 00 00 00 00 00 00 00 00 40
00 00 00 00 00 00 00 00 00 00 00 00 00 00 10 40
9a 99 99 99 99 99 01 40 00 00 00 00 00 00 18 c0
9a 99 99 99 99 99 11 c0 33 33 33 33 33 33 21 40
cd cc cc cc cc cc 10 40 33 33 33 33 33 33 03 c0
33 33 33 33 33 33 1b 40 74 03 00 00 00 00 00 00
00 00 00 14 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 22 40 00 00 00 00 00 00 1c 40 00 00 00
00 00 00 2a 40 00 00 00 00 00 00 f0 bf 71 04 00
00 00 00 00 00 00 00 00 14 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 22 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 22 40 00 00 00 00 00 00
1c 40 00 00 00 00 00 00 14 40 00 00 00 00 00 00
1c 40 63 02 00 00 00 00 00 00 00 00 00 14 40 00
00 00 00 00 00 08 40 00 00 00 00 00 00 22 40 00
00 00 00 00 00 1c 40 70 05 00 00 00 00 00 00 00
00 00 14 40 00 00 00 00 00 00 f0 bf 00 00 00 00
00 00 1c 40 34 33 33 33 33 33 f3 3f 00 00 00 00
00 00 08 c0 9a 99 99 99 99 99 15 c0 33 33 33 33
33 33 27 40 9a 99 99 99 99 99 09 40 34 33 33 33
33 33 e3 3f 33 33 33 33 33 33 17 40 74 03 00 00
00 c3 7f 8e f4 68 d5 13 40 e3 f7 9c 3c c9 8b 08
40 12 13 81 9e 70 ce 21 40 7b e1 b9 4e a7 7d 1c
40 a1 b5 b4 90 64 06 2a 40 d9 56 4a b1 73 4b ea
bf 71 04 00 00 00 c3 7f 8e f4 68 d5 13 40 e3 f7
9c 3c c9 8b 08 40 dc 02 7f 38 83 ea 21 40 0c b7
94 a4 13 fc 08 40 12 13 81 9e 70 ce 21 40 7b e1
b9 4e a7 7d 1c 40 2e a0 92 c0 43 9d 13 40 e6 01
be 1a 82 45 1c 40 63 02 00 00 00 c3 7f 8e f4 68
d5 13 40 e3 f7 9c 3c c9 8b 08 40 12 13 81 9e 70
ce 21 40 7b e1 b9 4e a7 7d 1c 40 70 05 00 00 00
57 5f 8a 28 8e 0d 14 40 1e 50 08 f1 c6 cd ed bf
5a 67 c4 a3 7b ee 1b 40 36 24 9c 67 c1 bb f4 3f
46 6d b2 94 d4 67 07 c0 ba 0f 2d 82 30 c3 15 c0
34 8f d6 12 2f 1c 27 40 4b 1a 34 8e a0 de 0a 40
a1 e5 e8 d3 73 a7 e0 3f 2c 4a d4 55 10 3b 17 40
Terminal:
$ ./a.out input_mix.bin output_mix.bin
74 03 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00
00 00 00 00 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 10 40 00 00 00 00 00 00 14 40 00 00 00
00 00 00 00 00 71 04 00 00 00 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 00 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 10 40 00 00 00 00 00 00
f0 3f 00 00 00 00 00 00 10 40 63 02 00 00 00 00
00 00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00
00 00 00 00 00 08 40 00 00 00 00 00 00 10 40 70
05 00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99
99 99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99
99 99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc
cc cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33
33 33 0b 40 74 03 00 00 00 00 00 00 00 00 00 00
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 18
40 00 00 00 00 00 00 20 40 00 00 00 00 00 00 24
40 00 00 00 00 00 00 00 00 71 04 00 00 00 00 00
00 00 00 00 00 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 18 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 18 40 00 00 00 00 00 00 20 40 00 00
00 00 00 00 00 40 00 00 00 00 00 00 20 40 63 02
00 00 00 00 00 00 00 00 00 00 40 00 00 00 00 00
00 10 40 00 00 00 00 00 00 18 40 00 00 00 00 00
00 20 40 70 05 00 00 00 00 00 00 00 00 00 00 40
00 00 00 00 00 00 00 00 00 00 00 00 00 00 10 40
9a 99 99 99 99 99 01 40 00 00 00 00 00 00 18 c0
9a 99 99 99 99 99 11 c0 33 33 33 33 33 33 21 40
cd cc cc cc cc cc 10 40 33 33 33 33 33 33 03 c0
33 33 33 33 33 33 1b 40 74 03 00 00 00 00 00 00
00 00 00 14 40 00 00 00 00 00 00 08 40 00 00 00
00 00 00 22 40 00 00 00 00 00 00 1c 40 00 00 00
00 00 00 2a 40 00 00 00 00 00 00 f0 bf 71 04 00
00 00 00 00 00 00 00 00 14 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 22 40 00 00 00 00 00 00
08 40 00 00 00 00 00 00 22 40 00 00 00 00 00 00
1c 40 00 00 00 00 00 00 14 40 00 00 00 00 00 00
1c 40 63 02 00 00 00 00 00 00 00 00 00 14 40 00
00 00 00 00 00 08 40 00 00 00 00 00 00 22 40 00
00 00 00 00 00 1c 40 70 05 00 00 00 00 00 00 00
00 00 14 40 00 00 00 00 00 00 f0 bf 00 00 00 00
00 00 1c 40 34 33 33 33 33 33 f3 3f 00 00 00 00
00 00 08 c0 9a 99 99 99 99 99 15 c0 33 33 33 33
33 33 27 40 9a 99 99 99 99 99 09 40 34 33 33 33
33 33 e3 3f 33 33 33 33 33 33 17 40 74 03 00 00
00 c3 7f 8e f4 68 d5 13 40 e3 f7 9c 3c c9 8b 08
40 12 13 81 9e 70 ce 21 40 7b e1 b9 4e a7 7d 1c
40 a1 b5 b4 90 64 06 2a 40 d9 56 4a b1 73 4b ea
bf 71 04 00 00 00 c3 7f 8e f4 68 d5 13 40 e3 f7
9c 3c c9 8b 08 40 dc 02 7f 38 83 ea 21 40 0c b7
94 a4 13 fc 08 40 12 13 81 9e 70 ce 21 40 7b e1
b9 4e a7 7d 1c 40 2e a0 92 c0 43 9d 13 40 e6 01
be 1a 82 45 1c 40 63 02 00 00 00 c3 7f 8e f4 68
d5 13 40 e3 f7 9c 3c c9 8b 08 40 12 13 81 9e 70
ce 21 40 7b e1 b9 4e a7 7d 1c 40 70 05 00 00 00
57 5f 8a 28 8e 0d 14 40 1e 50 08 f1 c6 cd ed bf
5a 67 c4 a3 7b ee 1b 40 36 24 9c 67 c1 bb f4 3f
46 6d b2 94 d4 67 07 c0 ba 0f 2d 82 30 c3 15 c0
34 8f d6 12 2f 1c 27 40 4b 1a 34 8e a0 de 0a 40
a1 e5 e8 d3 73 a7 e0 3f 2c 4a d4 55 10 3b 17 40
$
Pseudo Code
#include <iostream>
#include <iomanip>
#include <fstream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// length of the complex number
double length() const;
// angle of the complex number in radians
// use `atan2` to compute the angle by the formula `atan(imag/real)`
// and use `NAN` for 0/0 case
// `atan2` ref: https://en.cppreference.com/w/cpp/numeric/math/atan2
// `NAN` ref: https://en.cppreference.com/w/cpp/numeric/math/NAN
double angle() const;
// write data members in binary format
// note: be careful about the type used in `.write()` function
void write_binary_record(ostream &arg_os);
// read data members in binary format
// note: use `.read()` to get the double in binary format,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
void read_binary_record(istream &arg_is);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
// utility function to check if the transformation is valid
// hint: use `isnan` to check the angle is valid or not
// ref: https://en.cppreference.com/w/cpp/numeric/math/isnan
bool _check_transform(const Complex &arg_trans_c, const char &arg_op);
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
virtual void parse_geometry(ifstream &arg_ifs);
// apply transformation to the geometry
void transform_geometry(const Complex &arg_trans_c, const char &arg_op);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
// Ref: https://stackoverflow.com/q/9621893
void print_output_file(int argc, char *argv[])
{
ifstream ans_ifs(argv[2], ios::in | ios::binary);
if (!ans_ifs)
{
cout << "Error: Cannot open output file" << endl;
exit(1);
}
char ans_block = 0;
unsigned offset_count = 0;
ans_ifs.read(&ans_block, 1);
while (!ans_ifs.eof())
{
int z = ans_block & 0xff;
cout << std::hex
<< std::setfill('0')
<< std::setw(2)
<< z
<< " ";
offset_count++;
if (offset_count % 16 == 0)
{
cout << endl;
}
ans_ifs.read(&ans_block, 1);
}
cout << endl;
ans_ifs.close();
}
int main(int argc, char *argv[])
{
char input;
vector<Geometry_Comp *> geo_ptr_array;
Geometry_Comp *geo_ptr;
Complex trans_c;
char trans_op;
string input_file_path(argv[1]);
string output_file_path(argv[2]);
// open & check input file
// open & check output file
while (infile.get(input))
{
// check the geometry type
switch (input)
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
case 'r':
case 'z':
case 'm':
break;
default:
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
if (input == 't' || input == 'q' || input == 'p' || input == 'c')
{
// parse the cin to the geometry
geo_ptr->parse_geometry(infile);
// print the geometry
geo_ptr->print_geometry(outfile);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else if (input == 'r' || input == 'z' || input == 'm')
{
trans_c.read_binary_record(infile);
// transform the geometry using operator and complex
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->transform_geometry(trans_c, input);
// print transformed geometry
geo_ptr_array[i]->print_geometry(outfile);
}
}
else
{
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
}
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
// close input and output file
print_output_file(argc, argv);
return 0;
}
Reference Code:
TA
#include <iostream>
#include <iomanip>
#include <fstream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// length of the complex number
double length() const;
// angle of the complex number in radians
// use `atan2` to compute the angle by the formula `atan(imag/real)`
// and use `NAN` for 0/0 case
// `atan2` ref: https://en.cppreference.com/w/cpp/numeric/math/atan2
// `NAN` ref: https://en.cppreference.com/w/cpp/numeric/math/NAN
double angle() const;
// write data members in binary format
// note: be careful about the type used in `.write()` function
void write_binary_record(ostream &arg_os);
// read data members in binary format
// note: use `.read()` to get the double in binary format,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
void read_binary_record(istream &arg_is);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
// utility function to check if the transformation is valid
// hint: use `isnan` to check the angle is valid or not
// ref: https://en.cppreference.com/w/cpp/numeric/math/isnan
bool _check_transform(const Complex &arg_trans_c, const char &arg_op);
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
virtual void parse_geometry(ifstream &arg_ifs);
// apply transformation to the geometry
void transform_geometry(const Complex &arg_trans_c, const char &arg_op);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
// Ref: https://stackoverflow.com/q/9621893
void print_output_file(int argc, char *argv[])
{
ifstream ans_ifs(argv[2], ios::in | ios::binary);
if (!ans_ifs)
{
cout << "Error: Cannot open output file" << endl;
exit(1);
}
char ans_block = 0;
unsigned offset_count = 0;
ans_ifs.read(&ans_block, 1);
while (!ans_ifs.eof())
{
int z = ans_block & 0xff;
cout << std::hex
<< std::setfill('0')
<< std::setw(2)
<< z
<< " ";
offset_count++;
if (offset_count % 16 == 0)
{
cout << endl;
}
ans_ifs.read(&ans_block, 1);
}
cout << endl;
ans_ifs.close();
}
// Complex class implementation
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
// Copy constructor
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
// assignment operator
Complex &Complex::operator=(const Complex &arg_c)
{
if (this == &arg_c) // self-assignment
return *this;
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
// add assignment operator
Complex &Complex::operator+=(const Complex &arg_c)
{
m_real += arg_c.m_real;
m_imag += arg_c.m_imag;
return *this;
}
// multiply assignment operator
Complex &Complex::operator*=(const Complex &arg_c)
{
double real = m_real * arg_c.m_real - m_imag * arg_c.m_imag;
double imag = m_real * arg_c.m_imag + m_imag * arg_c.m_real;
m_real = real;
m_imag = imag;
return *this;
}
// length of the complex number
double Complex::length() const
{
return sqrt(m_real * m_real + m_imag * m_imag);
}
// angle of the complex number in radians
double Complex::angle() const
{
if (m_real == 0 && m_imag == 0)
{
return NAN;
}
return atan2(m_imag, m_real);
}
// write data members in binary format
// note: be careful about the type used in `.write()` function
void Complex::write_binary_record(ostream &arg_os)
{
arg_os.write((char *)&m_real, sizeof(double));
arg_os.write((char *)&m_imag, sizeof(double));
}
// read data members in binary format
// note: use `.read()` to get the double in binary format,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
void Complex::read_binary_record(istream &arg_is)
{
double input_real, input_imag;
arg_is.read((char *)&input_real, sizeof(double));
if (arg_is.fail())
{
error_and_exit();
}
arg_is.read((char *)&input_imag, sizeof(double));
if (arg_is.fail())
{
error_and_exit();
}
m_real = input_real;
m_imag = input_imag;
}
// Geometry_Comp class implementation
// check if the transformation is valid
bool Geometry_Comp::_check_transform(const Complex &arg_c, const char &arg_op)
{
// check if the operation is valid
if (arg_op == 'r' && (arg_c.length() != 1 || isnan(arg_c.angle())))
{
return false;
}
else if (arg_op == 'z' && (arg_c.m_real == 0 || arg_c.m_imag != 0))
{
return false;
}
else
{
return true;
}
}
// Constructor, initializes the array
Geometry_Comp::Geometry_Comp(const unsigned int &arg_num_of_vertex)
: m_comp_array(arg_num_of_vertex)
{
}
// Copy constructor
Geometry_Comp::Geometry_Comp(const Geometry_Comp &arg_gc)
: m_comp_array(arg_gc.m_comp_array)
{
}
// assignment operator
Geometry_Comp &Geometry_Comp::operator=(const Geometry_Comp &arg_gc)
{
if (this == &arg_gc) // self-assignment
return *this;
m_comp_array = arg_gc.m_comp_array;
return *this;
}
// print the geometry
void Geometry_Comp::print_geometry(ofstream &arg_ofs)
{
cout << "not implemented" << endl;
}
// parse the cin to the geometry
void Geometry_Comp::parse_geometry(ifstream &arg_ifs)
{
cout << "not implemented" << endl;
}
// apply transformation to the geometry
void Geometry_Comp::transform_geometry(const Complex &arg_c, const char &arg_op)
{
if (!(_check_transform(arg_c, arg_op)))
{
error_and_exit();
}
if (arg_op == 'm')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] += arg_c;
}
}
else if (arg_op == 'r' || arg_op == 'z')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] *= arg_c;
}
}
}
// set the geometry
void Geometry_Comp::set_geometry(const vector<Complex> &arg_comp_array)
{
m_comp_array = arg_comp_array;
}
// get the geometry array
vector<Complex> Geometry_Comp::get_geometry_array()
{
return m_comp_array;
}
// Triangle_Comp class implementation
// Constructor, initializes the array
Triangle_Comp::Triangle_Comp()
: Geometry_Comp(triangle_num_of_vertex)
{
}
// Copy constructor
Triangle_Comp::Triangle_Comp(const Triangle_Comp &arg_tc)
: Geometry_Comp(arg_tc)
{
}
// assignment operator
Triangle_Comp &Triangle_Comp::operator=(const Triangle_Comp &arg_tc)
{
if (this == &arg_tc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_tc);
return *this;
}
// print the geometry
void Triangle_Comp::print_geometry(ofstream &arg_ofs)
{
unsigned int num_of_vertex = m_comp_array.size();
arg_ofs.write("t", 1);
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (unsigned int i = 0; i < num_of_vertex; i++)
{
m_comp_array[i].write_binary_record(arg_ofs);
}
}
// parse the cin to the geometry
void Triangle_Comp::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num != triangle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
Complex c;
c.read_binary_record(arg_ifs);
if (arg_ifs.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Quadrilateral_Comp class implementation
// Constructor, initializes the array
Quadrilateral_Comp::Quadrilateral_Comp()
: Geometry_Comp(quadrilateral_num_of_vertex)
{
}
// Copy constructor
Quadrilateral_Comp::Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc)
: Geometry_Comp(arg_qc)
{
}
// assignment operator
Quadrilateral_Comp &Quadrilateral_Comp::operator=(const Quadrilateral_Comp &arg_qc)
{
if (this == &arg_qc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_qc);
return *this;
}
// print the geometry
void Quadrilateral_Comp::print_geometry(ofstream &arg_ofs)
{
arg_ofs.write("q", 1);
unsigned int num_of_vertex = m_comp_array.size();
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (int i = 0; i < quadrilateral_num_of_vertex; i++)
{
m_comp_array[i].write_binary_record(arg_ofs);
}
}
// parse the cin to the geometry
void Quadrilateral_Comp::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num != quadrilateral_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
Complex c;
c.read_binary_record(arg_ifs);
if (arg_ifs.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Polygon_Comp class implementation
// Constructor, initializes the array
Polygon_Comp::Polygon_Comp()
: Geometry_Comp()
{
}
// Copy constructor
Polygon_Comp::Polygon_Comp(const Polygon_Comp &arg_pc)
: Geometry_Comp(arg_pc)
{
}
// assignment operator
Polygon_Comp &Polygon_Comp::operator=(const Polygon_Comp &arg_pc)
{
if (this == &arg_pc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_pc);
return *this;
}
// print the geometry
void Polygon_Comp::print_geometry(ofstream &arg_ofs)
{
arg_ofs.write("p", 1);
unsigned int num_of_vertex = m_comp_array.size();
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i].write_binary_record(arg_ofs);
}
}
// parse the cin to the geometry
void Polygon_Comp::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num < triangle_num_of_vertex)
{
error_and_exit();
}
m_comp_array.resize(vertex_num);
for (int i = 0; i < vertex_num; i++)
{
Complex c;
c.read_binary_record(arg_ifs);
if (arg_ifs.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// Circle_Comp class implementation
// Constructor, initializes the array
Circle_Comp::Circle_Comp()
: Geometry_Comp(circle_num_of_vertex)
{
}
// Copy constructor
Circle_Comp::Circle_Comp(const Circle_Comp &arg_cc)
: Geometry_Comp(arg_cc)
{
}
// assignment operator
Circle_Comp &Circle_Comp::operator=(const Circle_Comp &arg_cc)
{
if (this == &arg_cc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_cc);
return *this;
}
// print the geometry
void Circle_Comp::print_geometry(ofstream &arg_ofs)
{
arg_ofs.write("c", 1);
unsigned int num_of_vertex = m_comp_array.size();
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (int i = 0; i < circle_num_of_vertex; i++)
{
m_comp_array[i].write_binary_record(arg_ofs);
}
}
// parse the cin to the geometry
void Circle_Comp::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num != circle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
Complex c;
c.read_binary_record(arg_ifs);
if (arg_ifs.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
int main(int argc, char *argv[])
{
char input;
vector<Geometry_Comp *> geo_ptr_array;
Geometry_Comp *geo_ptr;
Complex trans_c;
char trans_op;
string input_file_path(argv[1]);
string output_file_path(argv[2]);
ifstream infile(input_file_path, ios::in | ios::binary);
if (!infile)
{
cout << "Input file cannot open." << endl;
return -1;
}
ofstream outfile(output_file_path, ios::out | ios::trunc | ios::binary);
if (!outfile)
{
cout << "Output file cannot open." << endl;
return -1;
}
while (infile.get(input))
{
// check the geometry type
switch (input)
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
case 'r':
case 'z':
case 'm':
break;
default:
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
if (input == 't' || input == 'q' || input == 'p' || input == 'c')
{
// parse the cin to the geometry
geo_ptr->parse_geometry(infile);
// print the geometry
geo_ptr->print_geometry(outfile);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else if (input == 'r' || input == 'z' || input == 'm')
{
trans_c.read_binary_record(infile);
// transform the geometry using operator and complex
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->transform_geometry(trans_c, input);
// print transformed geometry
geo_ptr_array[i]->print_geometry(outfile);
}
}
else
{
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
}
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
infile.close();
outfile.close();
print_output_file(argc, argv);
return 0;
}
Convert Text Version Input to Binary Version Input
/*** convert text version input to binary version input ***/
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>
using namespace std;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
int main(int argc, char *argv[])
{
if (argc != 3)
{
cout << "Usage: txt_to_bin <input_file> <output_file>" << endl;
return 1;
}
ifstream input_file(argv[1]);
ofstream output_file(argv[2], ios::binary | ios::trunc);
if (!input_file.is_open())
{
cout << "Could not open input file" << endl;
return 1;
}
if (!output_file.is_open())
{
cout << "Could not open output file" << endl;
return 1;
}
string line, temp;
unsigned num_of_vertices = 1;
while (getline(input_file, line))
{
// check the geometry type
switch (line[0])
{
case 't':
case 'q':
case 'p':
case 'c':
// get the number of vertices from the next line
getline(input_file, temp);
num_of_vertices = stoul(temp);
break;
case 'r':
case 'z':
case 'm':
num_of_vertices = 1;
break;
default:
error_and_exit();
}
// write the geometry type
char geometry_type = line[0];
output_file.write(&geometry_type, 1);
// write the number of vertices
if (line[0] == 't' || line[0] == 'q' || line[0] == 'p' || line[0] == 'c')
{
output_file.write((char *)&num_of_vertices, sizeof(unsigned));
}
// convert the lines to binary
for (int i = 0; i < num_of_vertices; i++)
{
getline(input_file, line);
stringstream ss(line);
double real, imag;
ss >> real >> imag;
output_file.write((char *)&real, sizeof(double));
output_file.write((char *)&imag, sizeof(double));
}
}
input_file.close();
output_file.close();
return 0;
}
Convert Binary Version Input/Output to Human-readable Input/Output & Dump HEX File
/*** convert binary version input/output to
* human-readable input/output & dump hex file ***/
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>
#include <iomanip>
using namespace std;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
int main(int argc, char *argv[])
{
if (argc != 3)
{
cout << "Usage: bin_to_txt <input_file> <output_file>" << endl;
return 1;
}
ifstream input_file(argv[1], ios::binary);
ofstream output_file(argv[2], ios::trunc);
if (!input_file.is_open())
{
cout << "Could not open input file" << endl;
return 1;
}
if (!output_file.is_open())
{
cout << "Could not open output file" << endl;
return 1;
}
char input;
unsigned num_of_vertices = 1;
while (input_file.get(input))
{
// check the geometry type
switch (input)
{
case 't':
case 'q':
case 'p':
case 'c':
// get the number of vertices from the next line
input_file.read((char *)&num_of_vertices, sizeof(unsigned));
break;
case 'r':
case 'z':
case 'm':
num_of_vertices = 1;
break;
default:
error_and_exit();
}
// write the geometry type
char geometry_type = input;
output_file << "# " << geometry_type << endl;
// write the number of vertices
if (geometry_type == 't' || geometry_type == 'q'
|| geometry_type == 'p' || geometry_type == 'c')
{
output_file << "# " << num_of_vertices << endl;
}
// convert the lines to binary
for (int i = 0; i < num_of_vertices; i++)
{
double real, imag;
input_file.read((char *)&real, sizeof(double));
input_file.read((char *)&imag, sizeof(double));
output_file << "# " << setprecision(15) << fixed
<< real << " " << imag << endl;
}
}
input_file.close();
input_file.open(argv[1], ios::binary);
output_file << "# Hex dump" << endl;
char file_block = 0;
unsigned offset_count = 0;
input_file.read(&file_block, 1);
while (!input_file.eof())
{
int z = file_block & 0xff;
output_file << std::hex
<< std::setfill('0')
<< std::setw(2)
<< z
<< " ";
offset_count++;
if (offset_count % 16 == 0)
{
output_file << endl;
}
input_file.read(&file_block, 1);
}
output_file << endl;
output_file.close();
return 0;
}
Advanced I/O & Exception Handling
Slides version: lecture15_slides.html Website version: lecture15.html
- Detail in
iostream,fstream&stringstream- Stream Operator & Manipulator
- Stream Status & Error Handling
- Exception & Exception Handling
- What is an exception?
- How to handle exceptions?
- How many types of exceptions?
std::exceptionclass
iostream,fstream& exception handling
- Example: Exception Handling,
iostream&fstreamError Handling - Practices
Stream Operator & Manipulator
<< & >> stream operator
Discussed in lecture14
Stream Manipulator
Ref: Manipulators in C++ with Examples
There are two types of manipulators in C++:
- Manipulators without arguments:
- endl (output
\nand flush), ws (consume whitespace), ends (output\0), flush (flush output buffer to terminal)
- endl (output
- Manipulators with Arguments: Some of the manipulators are used with the argument like
setw(20),setfill(*), and many more.
- In
<ios>:(no)boolalpha,(no)uppercase,(no)showbase,(no)showpos,(no)showpoint,(no)skipws,(no)unitbuf,internal,left,right,hex,dec,oct,fixed,scientific
- In
<iomanip>:setw(val),setfill(c),setprecision(val),setbase(val),setiosflags(flag),resetiosflags(m)
(no)boolalpha
Ref: std::boolalpha, std::noboolalpha
#include <sstream>
#include <iostream>
int main()
{
// boolalpha output
std::cout << std::boolalpha
<< "boolalpha true: " << true << '\n'
<< "boolalpha false: " << false << '\n';
std::cout << std::noboolalpha
<< "noboolalpha true: " << true << '\n'
<< "noboolalpha false: " << false << '\n';
// boolalpha parse
bool b1, b2;
std::istringstream is("true false");
is >> std::boolalpha >> b1 >> b2;
std::cout << '\"' << is.str() << "\" parsed as " << b1 << ' ' << b2 << '\n';
}
(no)uppercase, (no)showbase
Ref: std::showbase, std::noshowbase, std::uppercase, std::nouppercase
#include <sstream>
#include <locale>
#include <iostream>
#include <iomanip>
int main()
{
// showbase affects the output of octals and hexadecimals
std::cout << std::hex
<< "showbase: " << std::showbase << 42 << '\n'
<< "noshowbase: " << std::noshowbase << 42 << '\n';
// uppercase affects the output of hexadecimals
std::cout << std::hex << std::showbase
<< "0x2a with uppercase: " << std::uppercase << 0x2a << '\n'
<< "0x2a with nouppercase: " << std::nouppercase << 0x2a << '\n'
<< "1e-10 with uppercase: " << std::uppercase << 1e-10 << '\n'
<< "1e-10 with nouppercase: " << std::nouppercase << 1e-10 << '\n';
}
(no)showpos, (no)showpoint
Ref: std::showpos, std::noshowpos, std::showpoint, std::noshowpoint
#include <iostream>
int main()
{
std::cout << "1.0 with showpoint: " << std::showpoint << 1.0 << '\n'
<< "1.0 with noshowpoint: " << std::noshowpoint << 1.0 << '\n';
std::cout
<< "showpos: " << std::showpos << 42 << ' ' << 3.14 << ' ' << 0 << '\n'
<< "noshowpos: " << std::noshowpos << 42 << ' ' << 3.14 << ' ' << 0 << '\n';
}
(no)skipws
Ref: std::skipws, std::noskipws
#include <iostream>
#include <sstream>
int main()
{
char c1, c2, c3;
std::istringstream("a b c") >> c1 >> c2 >> c3;
std::cout << "Default behavior: c1 = " << c1 << " c2 = " << c2 << " c3 = " << c3 << '\n';
std::istringstream("a b c") >> std::noskipws >> c1 >> c2 >> c3;
std::cout << "noskipws behavior: c1 = " << c1 << " c2 = " << c2 << " c3 = " << c3 << '\n';
}
internal, left, right
Ref: std::left, std::right, std::internal
#include <iostream>
#include <iomanip>
#include <locale>
int main()
{
std::cout.imbue(std::locale("en_US.utf8"));
std::cout << "Default positioning:\n"
<< std::setfill('*')
<< std::setw(12) << -1.23 << '\n'
<< std::setw(12) << std::hex << std::showbase << 42 << '\n'
<< std::setw(12) << std::put_money(123, true) << "\n\n";
std::cout << "Left positioning:\n"
<< std::left
<< std::setw(12) << -1.23 << '\n'
<< std::setw(12) << 42 << '\n'
<< std::setw(12) << std::put_money(123, true) << "\n\n";
std::cout << "Internal positioning:\n"
<< std::internal
<< std::setw(12) << -1.23 << '\n'
<< std::setw(12) << 42 << '\n'
<< std::setw(12) << std::put_money(123, true) << "\n\n";
std::cout << "Right positioning:\n"
<< std::right
<< std::setw(12) << -1.23 << '\n'
<< std::setw(12) << 42 << '\n'
<< std::setw(12) << std::put_money(123, true) << '\n';
}
hex, dec, oct
Ref: std::dec, std::hex, std::oct
#include <iostream>
#include <sstream>
#include <bitset>
int main()
{
std::cout << "The number 42 in octal: " << std::oct << 42 << '\n'
<< "The number 42 in decimal: " << std::dec << 42 << '\n'
<< "The number 42 in hex: " << std::hex << 42 << '\n';
int n;
std::istringstream("2A") >> std::hex >> n;
std::cout << std::dec << "Parsing \"2A\" as hex gives " << n << '\n';
// the output base is sticky until changed
std::cout << std::hex << "42 as hex gives " << 42
<< " and 21 as hex gives " << 21 << '\n';
// Note: there is no I/O manipulator that sets up a stream to print out
// numbers in binary format (e.g. bin). If binary output is necessary
// the std::bitset trick can be used:
std::cout << "The number 42 in binary: " << std::bitset<8>{42} << '\n';
}
fixed, scientific
Ref: std::fixed, std::scientific
#include <iostream>
#include <iomanip>
#include <sstream>
enum class cap { title, middle, end };
void print(const char* text, double num, cap c)
{
if (c == cap::title) std::cout <<
"┌──────────┬────────────┬──────────────────────────┐\n"
"│ number │ iomanip │ representation │\n"
"├──────────┼────────────┼──────────────────────────┤\n"
;
std::cout << std::left
<< "│ " << std::setw(8) << text << " │ fixed │ "
<< std::setw(24) << std::fixed << num << " │\n"
<< "│ " << std::setw(8) << text << " │ scientific │ "
<< std::setw(24) << std::scientific << num << " │\n"
<< "│ " << std::setw(8) << text << " │ hexfloat │ "
<< std::setw(24) << std::hexfloat << num << " │\n"
<< "│ " << std::setw(8) << text << " │ default │ "
<< std::setw(24) << std::defaultfloat << num << " │\n"
;
std::cout << (c != cap::end ?
"├──────────┼────────────┼──────────────────────────┤\n" :
"└──────────┴────────────┴──────────────────────────┘\n" );
}
int main()
{
print("0.0", 0.0, cap::title);
print("0.01", 0.01, cap::middle);
print("0.00001", 0.00001, cap::end);
// Note; choose clang for correct output
double f;
std::istringstream("0x1.8p+0") >> f;
std::cout << "Parsing 0x1.8p+0 gives " << f << '\n';
std::istringstream("0x1P-1022") >> f;
std::cout << "Parsing 0x1P-1022 gives " << f << '\n';
}
setw(val), setfill(c)
Ref: std::setw, std::setfill
#include <sstream>
#include <iostream>
#include <iomanip>
int main()
{
std::cout << "default fill: [" << std::setw(10) << 42 << "]\n"
<< "setfill('*'): [" << std::setfill('*')
<< std::setw(10) << 42 << "]\n";
std::cout << "no setw: [" << 42 << "]\n"
<< "setw(6): [" << std::setw(6) << 42 << "]\n"
<< "setw(6), several elements: [" << 89 << std::setw(6) << 12 << 34 << "]\n";
std::istringstream is("hello, world");
char arr[10];
is >> std::setw(6) >> arr;
std::cout << "Input from \"" << is.str() << "\" with setw(6) gave \""
<< arr << "\"\n";
}
setprecision(val)
Ref: std::setprecision
#include <iostream>
#include <iomanip>
#include <cmath>
#include <limits>
int main()
{
const long double pi = std::acos(-1.L);
std::cout << "default precision (6): " << pi << '\n'
<< "std::setprecision(10): " << std::setprecision(10) << pi << '\n'
<< "max precision: "
<< std::setprecision(std::numeric_limits<long double>::digits10 + 1)
<< pi << '\n';
}
setbase(val), alias of std::oct, std::dec, std::hex
Ref: std::setbase
#include <iostream>
#include <sstream>
#include <iomanip>
int main()
{
std::cout << "Parsing string \"10 0x10 010\"\n";
int n1, n2, n3;
std::istringstream s("10 0x10 010");
s >> std::setbase(16) >> n1 >> n2 >> n3;
std::cout << "hexadecimal parse: " << n1 << ' ' << n2 << ' ' << n3 << '\n';
s.clear();
s.seekg(0);
s >> std::setbase(0) >> n1 >> n2 >> n3;
std::cout << "prefix-dependent parse: " << n1 << ' ' << n2 << ' ' << n3 << '\n';
std::cout << "hex output: " << std::setbase(16)
<< std::showbase << n1 << ' ' << n2 << ' ' << n3 << '\n';
}
setiosflags(flag), resetiosflags(m)
Ref: std::setiosflags, std::resetiosflags
#include <sstream>
#include <iostream>
#include <iomanip>
int main()
{
if (false)
{
std::cout << std::resetiosflags(std::ios_base::dec)
<< std::setiosflags(std::ios_base::hex | std::ios_base::uppercase | std::ios_base::showbase) << 42 << '\n';
}
else
{
std::istringstream in("10 010 10 010 10 010");
int n1, n2;
in >> std::oct >> n1 >> n2;
std::cout << "Parsing \"10 010\" with std::oct gives: " << n1 << ' ' << n2 << '\n';
in >> std::dec >> n1 >> n2;
std::cout << "Parsing \"10 010\" with std::dec gives: " << n1 << ' ' << n2 << '\n';
in >> std::resetiosflags(std::ios_base::basefield) >> n1 >> n2;
std::cout << "Parsing \"10 010\" with autodetect gives: " << n1 << ' ' << n2 << '\n';
}
}
Stream Status & Error Handling
Ref: std::basic_ios, std::ios_base::iostate
- 4 states:
.good(),.eof(),.fail(),.bad().good(): checks if no error has occurred i.e. I/O operations are available..eof(): checks if end-of-file has been reached..fail(): checks if an error has occurred..bad(): checks if a non-recoverable error has occurred.
all of them are based on ios_base::iostate
badbit:trueif the stream has an irrecoverable stream erroreofbit:trueif the stream's associated input sequence has reached end-of-filefailbit:trueif the stream has an input/output operation failed (formatting or extraction error)
When will badbit be set
The badbit is set by the following situations:
- Fails to insert a character into the output stream, for any reason.
operator<<encounter the end of the output stream before completing output.- Initialize a stream with a
NULLpointer. - called on a stream with a
NULLpointer buffer. - A
NULLpointer is passed as the argument. - Buffer opeartions are returned with EOF value.
- Every stream I/O function if an exception is thrown by any member function of the associated stream buffer.
- Failure to allocate memory.
When will eofbit be set
The eofbit is set by the following situations:
- Reaching the end of the stream, as opposed to reaching the specified terminating character.
When will failbit be set
The failbit is set by the following situations:
- Initialize a stream while the stream either
eofbitorbadbitis set. - Extract invalid characters/invalid format/no characters or extract a
NULLpointer. - Extract
basic_string::max_sizecharacters from the input stream. - If the end-of-file condition occurs on the input stream before all requested characters could be extracted.
seekgortellpon failure- The constructors of
fstream,ifstream, andofstreamthat takes a filename argument, if the file cannot be opened. fstream::open,ifstream::open, andofstream::openif the file cannot be opened.fstream::close,ifstream::close, andofstream::closeif the file cannot be closed.
Relation between iostate flags and stream status
eofbit | failbit | badbit | .good() | .fail() | .bad() | .eof() | operator bool() | operator!() |
|---|---|---|---|---|---|---|---|---|
false | false | false | true | false | false | false | true | false |
false | false | true | false | true | true | false | false | true |
false | true | false | false | true | false | false | false | true |
false | true | true | false | true | true | false | false | true |
true | false | false | false | false | false | true | true | false |
true | false | true | false | true | true | true | false | true |
true | true | false | false | true | false | true | false | true |
true | true | true | false | true | true | true | false | true |
Exception & Exception Handling
- What is an exception?
- How to handle exceptions?
- How many types of exceptions?
iostream,fstream& exception handling
What is an exception?
Ref: Exception Handling in C++
Exceptions are run-time anomalies or abnormal conditions that a program encounters during its execution. There are two types of exceptions: a) Synchronous b) Asynchronous (Ex: which are beyond the program's control, Disc failure etc).
How to handle exceptions?
In C++, exceptions are handled by the following statements:
try
{
// a exception variable, could be any type
// and could be used without declaration
exception_type e;
// statements to be executed
// if exception occurs, throw the exception
throw e;
}
catch (exception_type e)
{
// statements to handle any exception thrown
}
Example:
#include <iostream>
using namespace std;
int main()
{
int x = -1;
// Some code
cout << "Before try \n";
try
{
cout << "Inside try \n";
if (x < 0)
{
throw x;
cout << "After throw (Never executed) \n";
}
}
catch (int x)
{
cout << "Exception Caught \n";
}
cout << "After catch (Will be executed) \n";
return 0;
}
Example: multiple catch blocks & default catch block
#include <iostream>
using namespace std;
int main()
{
try
{
throw 10;
}
catch (char *excp)
{
cout << "Caught " << excp;
}
catch (...)
{
cout << "Default Exception\n";
}
return 0;
}
Example: uncaught exception
#include <iostream>
using namespace std;
int main()
{
try
{
// error, unhandled exception
throw 'a';
}
catch (int x)
{
cout << "Caught ";
}
return 0;
}
Example: Nesting of exceptions
#include <iostream>
using namespace std;
int main()
{
try
{
try
{
throw 20;
}
catch (int n)
{
cout << "Handle Partially ";
throw; // Re-throwing an exception
}
}
catch (int n)
{
cout << "Handle remaining ";
}
return 0;
}
Example: class & exception
#include <iostream>
using namespace std;
class Test
{
public:
Test() { cout << "Constructor of Test " << endl; }
~Test() { cout << "Destructor of Test " << endl; }
};
int main()
{
try
{
Test t1;
throw 10;
}
catch (int i)
{
cout << "Caught " << i << endl;
}
}
Example: class inheritance & exception
// C++ Program to demonstrate a catching of
// Derived exception and printing it successfully
#include <iostream>
using namespace std;
class Base
{
};
class Derived : public Base
{
};
int main()
{
Derived d;
// Some other functionalities
try
{
// Monitored code
throw d;
}
catch (Derived d)
{
// the derived class object should be caught before the base class object
// else the base class object will always be caught
cout << "Caught Derived Exception";
}
catch (Base b)
{
cout << "Caught Base Exception";
}
getchar(); // To read the next character
return 0;
}
How many types of exceptions?
There are three types of exceptions:
- any preliminary types (e.g.,
int,char,float, etc.)- Discussed in the previous section
- user-defined types (e.g.,
class,struct, etc.)- Discussed in the previous section
std::exception
std::exception
Ref: Exception header in C++ with examples
std::exception is the base class of all exceptions in C++ standard library.
| Exception | Description |
|---|---|
std::bad_alloc | Memory allocation failed |
std::bad_cast | Invalid type conversion |
std::bad_exception | Exception handling failed |
std::bad_typeid | Invalid typeid |
std::bad_function_call | Invalid function call |
std::bad_weak_ptr | Invalid weak pointer |
std::logic_error | Logic error |
std::runtime_error | Runtime error |
exception::what()
Ref: exception::what() in C++ with Examples
To get the description of the exception, use the what() member function.
The example below shows how to use the what() member function and how it works.
// C++ code for exception::what()
#include <iostream>
#include <exception>
using namespace std;
class geeksforgeeks : public exception
{
public:
const char *what() const noexcept
{
return "Hey!!";
}
};
// main method
int main()
{
// try block
try
{
throw geeksforgeeks();
}
// catch block to handle the errors
catch (exception &gfg)
{
cout << gfg.what();
}
return 0;
}
Example: std::bad_alloc
// C++ program to illustrate bad_alloc
// using class bad_alloc
#include <exception>
#include <iostream>
using namespace std;
// Function to illustrate bad_alloc
void createArray(long long N)
{
// Try Block
try
{
// Create an array of length N
int *array = new int[N];
// If created successfully then
// print the message
cout << "Array created successfully"
<< " of length " << N << " \n";
}
// Check if the memory
// was allocated or not
// using class bad_alloc
catch (bad_alloc &e)
{
// If not, print the error message
cout << e.what()
<< " for array of length "
<< N << " \n";
}
}
// Driver Code
int main()
{
// Function call to create an
// array of 1000 size
createArray(1000);
// Function call to create an
// array of 1000000000 size
createArray(10000000000);
return 0;
}
Example: std::logic_error
// C++ program to illustrate logic_error
#include <exception>
#include <iostream>
using namespace std;
// Function to find factorial of N and
// throws error if occurs
void findFactorial(int N)
{
// Initialise variable by 1
int factorial = 1;
// Check for errors
try
{
// If N is less than zero then,
// it shows errors as factorial
// of negative number can't be
// calculated
if (N < 0)
{
// Exception object which
// returns the message passed
// to it
throw invalid_argument(
"negative not allowed");
}
// Find factorial if no error occurs
for (int i = N; i > 0; i--)
{
factorial *= i;
}
cout << "Factorial of " << N
<< " is " << factorial << endl;
}
// Print the error message
catch (exception &e)
{
cout << e.what();
}
}
// Driver Code
int main()
{
// Function call to find factorial
// of 0
findFactorial(0);
// Function call to find factorial
// of 3
findFactorial(3);
// Function call to find factorial
// of -1
findFactorial(-1);
return 0;
}
Example: Divide by zero
Ref: Handling the Divide by Zero Exception in C++
// Program to depict how to handle
// divide by zero exception
#include <iostream>
#include <stdexcept> // To use runtime_error
using namespace std;
// Defining function Division
float Division(float num, float den)
{
// If denominator is Zero
// throw runtime_error
if (den == 0)
{
throw runtime_error("Math error: Attempted to divide by Zero\n");
}
// Otherwise return the result of division
return (num / den);
} // end Division
int main()
{
float numerator, denominator, result;
numerator = 12.5;
denominator = 0;
// try block calls the Division function
try
{
result = Division(numerator, denominator);
// this will not print in this example
cout << "The quotient is "
<< result << endl;
}
// catch block catches exception thrown
// by the Division function
catch (runtime_error &e)
{
// prints that exception has occurred
// calls the what function
// using runtime_error object
cout << "Exception occurred" << endl
<< e.what();
}
} // end main
iostream, fstream & exception handling
Ref: std::basic_ios::exceptions
To Handle stream .bad(), .fail() and .eof() flags with try ... catch block, use .exceptions() member function to set the exceptions to be thrown.
The type of exception thrown is ios_base::failure.
Example:
#include <iostream>
#include <fstream>
int main()
{
int ivalue;
try
{
std::ifstream in("in.txt");
in.exceptions(std::ifstream::failbit); // may throw
in >> ivalue; // may throw
}
catch (const std::ios_base::failure &fail)
{
// handle exception here
std::cout << fail.what() << '\n';
}
}
Example: Exception Handling, iostream & fstream Error Handling [Source]
Practices
- Try to read/write files in serveral stream formats.
std::string,std::hex,std::uppercase, etc.
- Try to handle errors in
std::fstreamandstd::iostream- fail to open file, read/write error, invalid format, etc.
- Try to throw/handle exceptions in user-defined class
- examples in lectrue 2 to lecture 12
Example: Exception Handling, iostream & fstream Error Handling
#include <iostream>
#include <fstream>
#include <exception>
using namespace std;
class Triangle_2D; // forward declaration
class Point_2D // the class name
// we use first upper case letter to indicate a class
{
private: // private data members & member functions
// Data members
// we use `m_` to indicate a data member
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// Member functions
// we use `_` to indicate a member function
// check if the point is valid
void _check_validity();
public: // public member functions
// Constructor
// Constructor & Default constructor
// initialize data members, with default values
// accessable to const object by default
Point_2D(const double &arg_x = 0, const double &arg_y = 0);
// Copy constructor
// copy the data members from the given object
// accessable to const object by default
Point_2D(const Point_2D &arg_point);
// Destructor
~Point_2D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// Member functions
// we use lower case letter to indicate a member function
// also, we just define the function declaration
// and leave the definition to the end of the class
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set(const double &arg_x, const double &arg_y);
// get the x coordinate and y coordinate
// accessable to const object
double get_x() const;
double get_y() const;
// // compare two points
bool operator==(const Point_2D &arg_point) const;
bool operator!=(const Point_2D &arg_point) const;
bool operator<(const Point_2D &arg_point) const;
bool operator>(const Point_2D &arg_point) const;
bool operator<=(const Point_2D &arg_point) const;
bool operator>=(const Point_2D &arg_point) const;
// assign the point with another point
Point_2D &operator=(const Point_2D &arg_point);
// friend class
friend class Triangle_2D;
// friend function
// print the x and y coordinate in format (x, y)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os, const Point_2D &arg_point);
// read the coordinate of a point from the input, format: (x, y) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Point_2D &arg_point);
};
// Triangle_2D class declaration
class Triangle_2D
{
private:
// define three points of the Triangle_2D
// in array of Point_2D format
Point_2D m_point[3];
// check & correct the Triangle_2D points to counterclockwise order
void _check_points();
public:
// Constructor
Triangle_2D(const double &arg_x0 = 0.0, const double &arg_y0 = 0.0,
const double &arg_x1 = 0.0, const double &arg_y1 = 0.0,
const double &arg_x2 = 0.0, const double &arg_y2 = 0.0);
// Copy constructor
Triangle_2D(const Triangle_2D &arg_triangle);
// Destructor
~Triangle_2D()
{
// do nothing
}
// modify the three points of the Triangle_2D
void set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2);
void set_point1(const double &arg_x0, const double &arg_y0);
void set_point2(const double &arg_x1, const double &arg_y1);
void set_point3(const double &arg_x2, const double &arg_y2);
void set_x0(const double &arg_x0);
void set_y0(const double &arg_y0);
void set_x1(const double &arg_x1);
void set_y1(const double &arg_y1);
void set_x2(const double &arg_x2);
void set_y2(const double &arg_y2);
// get the three points of the Triangle_2D
double get_x0() const;
double get_y0() const;
double get_x1() const;
double get_y1() const;
double get_x2() const;
double get_y2() const;
// calculate the area of the Triangle_2D
double area();
// print the Triangle_2D
// format: ((x0, y0), (x1, y1), (x2, y2))
friend std::ostream &operator<<(std::ostream &arg_os, const Triangle_2D &arg_tri);
// read the coordinate of a point from the input,
// format: ((x0, y0), (x1, y1), (x2, y2)) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Triangle_2D &arg_tri);
};
// function definition
// check if the point is valid
void Point_2D::_check_validity()
{
// check if the x coordinate is valid
if (m_x < 0)
{
// if not, throw an exception
throw std::logic_error("x coordinate is invalid");
}
// check if the y coordinate is valid
if (m_y < 0)
{
// if not, throw an exception
throw std::logic_error("y coordinate is invalid");
}
}
// Constructor & Default constructor
// initialize data members, with default values
Point_2D::Point_2D(const double &arg_x, const double &arg_y)
// use `: var_name1(arg_var_name1), var_name2(arg_var_name2)`
// to initialize data members
: m_x(arg_x),
m_y(arg_y)
{
// check if the point is valid
_check_validity();
}
// Copy constructor
// copy the data members from the given object
Point_2D::Point_2D(const Point_2D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y)
{
// check if the point is valid
_check_validity();
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_2D::set_x(const double &arg_x)
{
m_x = arg_x;
// check if the point is valid
_check_validity();
}
void Point_2D::set_y(const double &arg_y)
{
m_y = arg_y;
// check if the point is valid
_check_validity();
}
void Point_2D::set(const double &arg_x, const double &arg_y)
{
m_x = arg_x;
m_y = arg_y;
// check if the point is valid
_check_validity();
}
// get the x coordinate and y coordinate
// accessable to const object
double Point_2D::get_x() const
{
return m_x;
}
double Point_2D::get_y() const
{
return m_y;
}
// // compare two points
bool Point_2D::operator==(const Point_2D &arg_point) const
{
// if the x and y coordinates are equal,
// return true
return (m_x == arg_point.m_x && m_y == arg_point.m_y);
}
bool Point_2D::operator!=(const Point_2D &arg_point) const
{
return !(*this == arg_point);
}
bool Point_2D::operator<(const Point_2D &arg_point) const
{
// if the x coordinate is smaller than the other point,
// return true
if (m_x < arg_point.m_x)
{
return true;
}
// if the x coordinate is equal to the other point,
// check if the y coordinate is smaller than the other point
else if (m_x == arg_point.m_x)
{
// if the y coordinate is smaller, return true
if (m_y < arg_point.m_y)
{
return true;
}
// if the y coordinate is equal to the other point,
// return false
else if (m_y == arg_point.m_y)
{
return false;
}
// if the y coordinate is larger, return false
else
{
return false;
}
}
// if the x coordinate is larger, return false
else
{
return false;
}
}
bool Point_2D::operator>(const Point_2D &arg_point) const
{
return !(*this < arg_point || *this == arg_point);
}
bool Point_2D::operator<=(const Point_2D &arg_point) const
{
return (*this < arg_point || *this == arg_point);
}
bool Point_2D::operator>=(const Point_2D &arg_point) const
{
return !(*this < arg_point);
}
// assign the point with another point
Point_2D &Point_2D::operator=(const Point_2D &arg_point)
{
// check if the point is valid
_check_validity();
// assign the x and y coordinate
m_x = arg_point.m_x;
m_y = arg_point.m_y;
// check if the point is valid
_check_validity();
return *this;
}
// print the point in the format (x, y)
std::ostream &operator<<(std::ostream &arg_os, const Point_2D &arg_point)
{
arg_os << "(" << arg_point.m_x << ", " << arg_point.m_y << ")";
return arg_os;
}
// read the coordinate of a point from the input, format: (x, y) and ignore space
std::istream &operator>>(std::istream &arg_is, Point_2D &arg_point)
{
string str_x, str_y, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (!temp.empty())
{
throw std::runtime_error("Invalid input");
}
if (getline(arg_is, str_x, ','))
{
if (str_x.empty())
{
throw std::runtime_error("Invalid input");
}
if (getline(arg_is, str_y, ')'))
{
if (str_y.empty())
{
throw std::runtime_error("Invalid input");
}
arg_point.m_x = stod(str_x);
arg_point.m_y = stod(str_y);
}
}
}
// check if the point is valid
arg_point._check_validity();
return arg_is;
}
// Triangle_2D class implementation
// check & correct the Triangle_2D points to counterclockwise order
void Triangle_2D::_check_points()
{
// sort the points in ascending order
for (int i = 0; i < 3; i++)
{
for (int j = i + 1; j < 3; j++)
{
if (m_point[i] > m_point[j])
{
// swap the points
Point_2D temp = m_point[i];
m_point[i] = m_point[j];
m_point[j] = temp;
}
}
}
// if the area is negative, swap the points
if (area() < 0.0)
{
Point_2D temp = m_point[0];
m_point[0] = m_point[1];
m_point[1] = temp;
}
}
// Constructor
Triangle_2D::Triangle_2D(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
: m_point{Point_2D(arg_x0, arg_y0),
Point_2D(arg_x1, arg_y1),
Point_2D(arg_x2, arg_y2)} // init the array with {}
{
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// Copy constructor
Triangle_2D::Triangle_2D(const Triangle_2D &arg_triangle)
: m_point{Point_2D(arg_triangle.m_point[0]),
Point_2D(arg_triangle.m_point[1]),
Point_2D(arg_triangle.m_point[2])} // init the array with {}
{
}
// set the three points of the Triangle_2D
void Triangle_2D::set_points(const double &arg_x0, const double &arg_y0,
const double &arg_x1, const double &arg_y1,
const double &arg_x2, const double &arg_y2)
{
m_point[0].set(arg_x0, arg_y0);
m_point[1].set(arg_x1, arg_y1);
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point1(const double &arg_x0, const double &arg_y0)
{
m_point[0].set(arg_x0, arg_y0);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point2(const double &arg_x1, const double &arg_y1)
{
m_point[1].set(arg_x1, arg_y1);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_point3(const double &arg_x2, const double &arg_y2)
{
m_point[2].set(arg_x2, arg_y2);
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x0(const double &arg_x0)
{
m_point[0].m_x = arg_x0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y0(const double &arg_y0)
{
m_point[0].m_y = arg_y0;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x1(const double &arg_x1)
{
m_point[1].m_x = arg_x1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y1(const double &arg_y1)
{
m_point[1].m_y = arg_y1;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_x2(const double &arg_x2)
{
m_point[2].m_x = arg_x2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
void Triangle_2D::set_y2(const double &arg_y2)
{
m_point[2].m_y = arg_y2;
// check & correct the Triangle_2D points to counterclockwise order
_check_points();
}
// get the three points of the Triangle_2D
double Triangle_2D::get_x0() const
{
return m_point[0].m_x;
}
double Triangle_2D::get_y0() const
{
return m_point[0].m_y;
}
double Triangle_2D::get_x1() const
{
return m_point[1].m_x;
}
double Triangle_2D::get_y1() const
{
return m_point[1].m_y;
}
double Triangle_2D::get_x2() const
{
return m_point[2].m_x;
}
double Triangle_2D::get_y2() const
{
return m_point[2].m_y;
}
// calculate the area of the Triangle_2D
double Triangle_2D::area()
{
// calculate the area of the Triangle_2D
return (m_point[0].m_x * m_point[1].m_y +
m_point[1].m_x * m_point[2].m_y +
m_point[2].m_x * m_point[0].m_y -
m_point[0].m_x * m_point[2].m_y -
m_point[1].m_x * m_point[0].m_y -
m_point[2].m_x * m_point[1].m_y) /
2.0;
}
// print the Triangle_2D
// format: ((x0, y0), (x1, y1), (x2, y2))
std::ostream &operator<<(std::ostream &arg_os, const Triangle_2D &arg_tri)
{
arg_os << "(";
for (int i = 0; i < 3; i++)
{
arg_os << arg_tri.m_point[i];
if (i < 2)
arg_os << ", ";
}
arg_os << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: ((x0, y0), (x1, y1), (x2, y2)) and ignore space
std::istream &operator>>(std::istream &arg_is, Triangle_2D &arg_tri)
{
string temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (!temp.empty())
{
throw std::runtime_error("Triangle_2D::operator>>: "
"the first character of the input "
"is not '('");
}
for (int i = 0; i < 3; i++)
{
arg_is >> ws >> arg_tri.m_point[i];
if (i < 2)
{
getline(arg_is, temp, ','); // ignore the ','
if (!temp.empty())
{
throw std::runtime_error("Triangle_2D::operator>>: "
"the character after the "
"coordinate is not ','");
}
}
}
getline(arg_is, temp, ')'); // ignore the last ')'
if (!temp.empty())
{
throw std::runtime_error("Triangle_2D::operator>>: "
"the character after the last "
"coordinate is not ')'");
}
}
// check & correct the Triangle_2D points to counterclockwise order
arg_tri._check_points();
return arg_is;
}
// main function
int main()
{
try
{
Triangle_2D t(1, 1, 2, 2, 0, 3);
cout << t << endl;
cout << "Area: " << t.area() << endl;
ofstream t_file("triangle.txt", ios::out | ios::trunc);
t_file.exceptions(ios::failbit | ios::badbit);
// reuse the `<<` operator to write the Triangle_2D to the file
t_file << t << endl;
t_file.close();
// read the Triangle_2D from the file
ifstream t_file_in("triangle.txt", ios::in);
t_file_in.exceptions(ios::failbit | ios::badbit);
Triangle_2D t_in;
t_file_in >> t_in;
cout << t_in << endl;
cout << "Area: " << t_in.area() << endl;
t_file_in.close();
}
catch (const std::exception &e)
{
std::cout << e.what() << '\n';
}
return 0;
}
Final Project: Geometry Processing
Final-1: Geometry Objects (50%)
-
Inputs:
- Input the dimensions (
dim) of the coordinate system. The dimension is anunsignedbetween 2 and 10. - Input the type of geometry object, one type per line, with the following types:
lfor linetfor trianglepfor polygon
- Input the number of vertices, one number per line, for each type of geometry object as shown above.
- line: 2
- triangle: 3
- polygon: \(n \in Z^+, n \ge 3\)
- Input the vertices, one vertex per line, seperate by a comma (
,), and withdimcoordinates indoubleformat.- line:
<double 1>,<double 2>,...,<double dim>⏎<double 1>,<double 2>,...,<double dim> - triangle:
<double 1>,<double 2>,...,<double dim>⏎<double 1>,<double 2>,...,<double dim>⏎<double 1>,<double 2>,...,<double dim> - polygon:
<double 1>,<double 2>,...,<double dim>⏎<double 1>,<double 2>,...,<double dim>⏎...
- line:
- Input Ctrl+D to finish the input.
- Windows: Ctrl+Z (will show
^Zon the screen) then Enter (⏎in Format) to finish the input.
- Windows: Ctrl+Z (will show
- Input the dimensions (
-
Outputs:
- The dimensions of the coordinate system.
- All geometric objects in the input, with the following information:
- Display the type of the object, the number of vertices, and the vertices.
- The format shold follow the descriptions in Format.
- The order of the vertices and coordinates should be the same as the input.
- Each coordinate should be displayed with default
doubleformat.
- Display the type of the object, the number of vertices, and the vertices.
- Print the dimension and all geometric objects after the input is finished, and exit the program.
-
File name:
final-1_<student_id>.cpp(e.g.final-1_106062802.cpp) -
The program will not have any user prompts, only print the result.
-
The program does not need to handle invalid inputs.
-
The program should base on the
mainfunction provided in the pseudo code. -
The program should be finished within 10 seconds. Any test cases will garuntee the program is finished within 10 seconds.
Format
<dim>⏎
<geometry type>⏎
n⏎
<double 1>,<double 2>,...,<double dim>⏎
<double 1>,<double 2>,...,<double dim>⏎
...
<double 1>,<double 2>,...,<double dim>⏎
<geometry type>⏎
n⏎
<double 1>,<double 2>,...,<double dim>⏎
<double 1>,<double 2>,...,<double dim>⏎
...
<double 1>,<double 2>,...,<double dim>⏎
^Z⏎
<dim>
<geometry type>
n
<double 1>,<double 2>,...,<double dim>
<double 1>,<double 2>,...,<double dim>
...
<double 1>,<double 2>,...,<double dim>
<geometry type>
n
<double 1>,<double 2>,...,<double dim>
<double 1>,<double 2>,...,<double dim>
...
<double 1>,<double 2>,...,<double dim>
Example
dim = 2
Triangle
$ ./a.out
2⏎
t⏎
3⏎
1.0,2.0⏎
3.0,4.0⏎
5.0,0.0⏎
^Z⏎
2
t
3
1,2
3,4
5,0
$
Line
$ ./a.out
2⏎
l⏎
2⏎
1.0,2.0⏎
3.0,4.0⏎
^Z⏎
2
l
2
1,2
3,4
$
Polygon
$ ./a.out
2⏎
p⏎
5⏎
1.0,0.0⏎
2.0,1.1⏎
-3.0,-2.2⏎
4.3,2.1⏎
-1.2,3.4⏎
^Z⏎
2
p
5
1,0
2,1.1
-3,-2.2
4.3,2.1
-1.2,3.4
$
Multiple Objects
$ ./a.out
2⏎
t⏎
3⏎
1.0,2.0⏎
3.0,4.0⏎
5.0,0.0⏎
l⏎
2⏎
1.0,2.0⏎
3.0,4.0⏎
p⏎
5⏎
1.0,0.0⏎
2.0,1.1⏎
-3.0,-2.2⏎
4.3,2.1⏎
-1.2,3.4⏎
^Z⏎
2
t
3
1,2
3,4
5,0
l
2
1,2
3,4
p
5
1,0
2,1.1
-3,-2.2
4.3,2.1
-1.2,3.4
$
dim = 3
Triangle
$ ./a.out
3⏎
t⏎
3⏎
1.0,2.0,3.0⏎
3.0,4.0,5.0⏎
5.0,0.0,1.0⏎
^Z⏎
3
t
3
1,2,3
3,4,5
5,0,1
$
Line
$ ./a.out
3⏎
l⏎
2⏎
1.0,2.0,3.0⏎
3.0,4.0,5.0⏎
^Z⏎
3
l
2
1,2,3
3,4,5
$
Polygon
$ ./a.out
3⏎
p⏎
5⏎
1.0,0.0,-1.0⏎
2.0,1.1,0.2⏎
-3.0,-2.2,-1.3⏎
4.3,2.1,0.1⏎
-1.2,3.4,-5.6⏎
^Z⏎
3
p
5
1,0,-1
2,1.1,0.2
-3,-2.2,-1.3
4.3,2.1,0.1
-1.2,3.4,-5.6
$
Multiple Objects
$ ./a.out
3⏎
t⏎
3⏎
1.0,2.0,3.0⏎
3.0,4.0,5.0⏎
5.0,0.0,1.0⏎
l⏎
2⏎
1.0,2.0,3.0⏎
3.0,4.0,5.0⏎
p⏎
5⏎
1.0,0.0,-1.0⏎
2.0,1.1,0.2⏎
-3.0,-2.2,-1.3⏎
4.3,2.1,0.1⏎
-1.2,3.4,-5.6⏎
^Z⏎
3
t
3
1,2,3
3,4,5
5,0,1
l
2
1,2,3
3,4,5
p
5
1,0,-1
2,1.1,0.2
-3,-2.2,-1.3
4.3,2.1,0.1
-1.2,3.4,-5.6
$
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
#include <exception>
using namespace std;
class Geometry_ND;
class Point_ND
{
private:
vector<double> m_coords;
unsigned m_dim;
friend class Geometry_ND;
public:
// Constructor, initializes dimension and coordinates
Point_ND(const unsigned &arg_dim = 2);
// Copy constructor
Point_ND(const Point_ND &arg_point);
// assignment operator
Point_ND &operator=(const Point_ND &arg_point);
// get coordinates
vector<double> get_coords() const;
// get dimension
unsigned get_dim() const;
// set coordinates
void set_coords(const vector<double> &arg_coords);
// cout `<<` operator for print Point_ND number
friend ostream &operator<<(ostream &arg_os, const Point_ND &arg_point);
// cin `>>` operator for input Point_ND number
friend istream &operator>>(istream &arg_is, Point_ND &arg_point);
// friend class
friend class Geometry_ND;
};
class Geometry_ND
{
protected:
// data members
vector<Point_ND> m_point_array;
unsigned m_dim;
public:
// Constructor, initializes the array
Geometry_ND(const unsigned &arg_dim = 2,
const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_ND(const Geometry_ND &arg_geometry);
// assignment operator
Geometry_ND &operator=(const Geometry_ND &arg_geometry);
// print the geometry
virtual void print_geometry();
// parse the cin to the geometry
virtual void parse_geometry(istream &arg_is);
// set the geometry
void set_geometry(const vector<Point_ND> &arg_point_array);
// get the geometry array
vector<Point_ND> get_geometry_array();
};
class Triangle_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Triangle_ND(const unsigned &arg_dim = 2);
// Copy constructor
Triangle_ND(const Triangle_ND &arg_triangle);
// assignment operator
Triangle_ND &operator=(const Triangle_ND &arg_triangle);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned triangle_num_of_vertex = 3;
class Polygon_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Polygon_ND(const unsigned &arg_dim = 2);
// Copy constructor
Polygon_ND(const Polygon_ND &arg_polygon);
// assignment operator
Polygon_ND &operator=(const Polygon_ND &arg_polygon);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
class Line_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Line_ND(const unsigned &arg_dim = 2);
// Copy constructor
Line_ND(const Line_ND &arg_line);
// assignment operator
Line_ND &operator=(const Line_ND &arg_line);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned line_num_of_vertex = 2;
int main()
{
vector<Geometry_ND *> geo_ptr_array;
string input;
unsigned dim;
Geometry_ND *geo_ptr;
// read dimension
// read geometry
while (getline(cin, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_ND(dim);
break;
case 'p':
geo_ptr = new Polygon_ND(dim);
break;
case 'l':
geo_ptr = new Line_ND(dim);
break;
}
if (input == "t" || input == "p" || input == "l")
{
// parse the cin to the geometry
geo_ptr->parse_geometry(cin);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
}
// print the geometry
// first, print the dimension
// second, print the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->print_geometry();
}
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
return 0;
}
Reference Code:
TA
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
#include <exception>
using namespace std;
class Geometry_ND;
class Point_ND
{
private:
vector<double> m_coords;
unsigned m_dim;
friend class Geometry_ND;
public:
// Constructor, initializes the array
Point_ND(const unsigned &arg_dim = 2);
// Copy constructor
Point_ND(const Point_ND &arg_point);
// assignment operator
Point_ND &operator=(const Point_ND &arg_point);
// get coordinates
vector<double> get_coords() const;
// get dimension
unsigned get_dim() const;
// set coordinates
void set_coords(const vector<double> &arg_coords);
// cout `<<` operator for print Point_ND number
friend ostream &operator<<(ostream &arg_os, const Point_ND &arg_point);
// cin `>>` operator for input Point_ND number
friend istream &operator>>(istream &arg_is, Point_ND &arg_point);
// friend class
friend class Geometry_ND;
};
class Geometry_ND
{
protected:
// data members
vector<Point_ND> m_point_array;
unsigned m_dim;
public:
// Constructor, initializes the array
Geometry_ND(const unsigned &arg_dim = 2,
const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_ND(const Geometry_ND &arg_geometry);
// assignment operator
Geometry_ND &operator=(const Geometry_ND &arg_geometry);
// print the geometry
virtual void print_geometry();
// parse the cin to the geometry
virtual void parse_geometry(istream &arg_is);
// set the geometry
void set_geometry(const vector<Point_ND> &arg_point_array);
// get the geometry array
vector<Point_ND> get_geometry_array();
};
class Triangle_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Triangle_ND(const unsigned &arg_dim = 2);
// Copy constructor
Triangle_ND(const Triangle_ND &arg_triangle);
// assignment operator
Triangle_ND &operator=(const Triangle_ND &arg_triangle);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned triangle_num_of_vertex = 3;
class Polygon_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Polygon_ND(const unsigned &arg_dim = 2);
// Copy constructor
Polygon_ND(const Polygon_ND &arg_polygon);
// assignment operator
Polygon_ND &operator=(const Polygon_ND &arg_polygon);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
class Line_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Line_ND(const unsigned &arg_dim = 2);
// Copy constructor
Line_ND(const Line_ND &arg_line);
// assignment operator
Line_ND &operator=(const Line_ND &arg_line);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
};
const unsigned line_num_of_vertex = 2;
// Point_ND class implementation
// Constructor
Point_ND::Point_ND(const unsigned &arg_dim)
: m_dim(arg_dim), m_coords(arg_dim)
{
}
// Copy constructor
Point_ND::Point_ND(const Point_ND &arg_point)
: m_dim(arg_point.m_dim), m_coords(arg_point.m_coords)
{
}
// assignment operator
Point_ND &Point_ND::operator=(const Point_ND &arg_point)
{
if (this != &arg_point)
{
m_dim = arg_point.m_dim;
m_coords = arg_point.m_coords;
}
return *this;
}
// get dimension
unsigned Point_ND::get_dim() const
{
return m_dim;
}
// get coordinates
vector<double> Point_ND::get_coords() const
{
return m_coords;
}
// set coordinates
void Point_ND::set_coords(const vector<double> &arg_coords)
{
m_coords = arg_coords;
}
// cout `<<` operator for print Point_ND number
ostream &operator<<(ostream &arg_os, const Point_ND &arg_point)
{
for (unsigned i = 0; i < arg_point.m_dim; i++)
{
if (i != 0)
{
arg_os << ",";
}
arg_os << arg_point.m_coords[i];
}
arg_os << flush;
return arg_os;
}
// cin `>>` operator for input Point_ND number
istream &operator>>(istream &arg_is, Point_ND &arg_point)
{
string line;
getline(arg_is, line);
istringstream iss(line);
for (unsigned i = 0; i < arg_point.m_dim; i++)
{
string buf;
double input_num;
getline(iss, buf, ',');
input_num = stod(buf);
arg_point.m_coords[i] = input_num;
}
return arg_is;
}
// Geometry_ND class implementation
// Constructor, initializes the array
Geometry_ND::Geometry_ND(const unsigned &arg_dim, const unsigned int &arg_num_of_vertex)
: m_dim(arg_dim), m_point_array(arg_num_of_vertex)
{
}
// Copy constructor
Geometry_ND::Geometry_ND(const Geometry_ND &arg_geometry)
: m_dim(arg_geometry.m_dim), m_point_array(arg_geometry.m_point_array)
{
}
// assignment operator
Geometry_ND &Geometry_ND::operator=(const Geometry_ND &arg_geometry)
{
if (this == &arg_geometry) // self-assignment
return *this;
m_point_array = arg_geometry.m_point_array;
return *this;
}
// print the geometry
void Geometry_ND::print_geometry()
{
throw runtime_error("print_geometry() is not implemented");
}
// parse the cin to the geometry
void Geometry_ND::parse_geometry(istream &arg_is)
{
throw runtime_error("parse_geometry() is not implemented");
}
// set the geometry
void Geometry_ND::set_geometry(const vector<Point_ND> &arg_point_array)
{
// check the dimension
for (unsigned i = 0; i < arg_point_array.size(); i++)
{
if (arg_point_array[i].get_dim() != m_dim)
{
throw runtime_error("The dimension of the geometry is not consistent");
}
}
m_point_array = arg_point_array;
}
// get the geometry array
vector<Point_ND> Geometry_ND::get_geometry_array()
{
return m_point_array;
}
// Triangle_ND class implementation
// Constructor, initializes the array
Triangle_ND::Triangle_ND(const unsigned &arg_dim)
: Geometry_ND(arg_dim, triangle_num_of_vertex)
{
}
// Copy constructor
Triangle_ND::Triangle_ND(const Triangle_ND &arg_triangle)
: Geometry_ND(arg_triangle)
{
}
// assignment operator
Triangle_ND &Triangle_ND::operator=(const Triangle_ND &arg_triangle)
{
if (this == &arg_triangle) // self-assignment
return *this;
Geometry_ND::operator=(arg_triangle);
return *this;
}
// print the geometry
void Triangle_ND::print_geometry()
{
cout << "t" << endl;
cout << m_point_array.size() << endl;
for (int i = 0; i < triangle_num_of_vertex; i++)
{
cout << m_point_array[i] << endl;
}
}
// parse the cin to the geometry
void Triangle_ND::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
stringstream ss(temp);
unsigned int vertex_num;
ss >> vertex_num;
if (vertex_num != triangle_num_of_vertex)
{
throw runtime_error("Triangle_ND::parse_geometry(): wrong vertex number");
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Point_ND point(m_dim);
ss >> point;
m_point_array[i] = point;
}
}
// Polygon_ND class implementation
// Constructor, initializes the array
Polygon_ND::Polygon_ND(const unsigned &arg_dim)
: Geometry_ND(arg_dim)
{
}
// Copy constructor
Polygon_ND::Polygon_ND(const Polygon_ND &arg_polygon)
: Geometry_ND(arg_polygon)
{
}
// assignment operator
Polygon_ND &Polygon_ND::operator=(const Polygon_ND &arg_polygon)
{
if (this == &arg_polygon) // self-assignment
return *this;
Geometry_ND::operator=(arg_polygon);
return *this;
}
// print the geometry
void Polygon_ND::print_geometry()
{
cout << "p" << endl;
cout << m_point_array.size() << endl;
for (int i = 0; i < m_point_array.size(); i++)
{
cout << m_point_array[i] << endl;
}
}
// parse the cin to the geometry
void Polygon_ND::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num < triangle_num_of_vertex)
{
throw runtime_error("Polygon_ND::parse_geometry(): the number of vertex is less than 3");
}
m_point_array.resize(vertex_num);
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Point_ND point(m_dim);
ss >> point;
m_point_array[i] = point;
}
}
// Line_ND class implementation
// Constructor, initializes the array
Line_ND::Line_ND(const unsigned &arg_dim)
: Geometry_ND(arg_dim, line_num_of_vertex)
{
}
// Copy constructor
Line_ND::Line_ND(const Line_ND &arg_line)
: Geometry_ND(arg_line)
{
}
// assignment operator
Line_ND &Line_ND::operator=(const Line_ND &arg_line)
{
if (this == &arg_line) // self-assignment
return *this;
Geometry_ND::operator=(arg_line);
return *this;
}
// print the geometry
void Line_ND::print_geometry()
{
cout << "l" << endl;
cout << m_point_array.size() << endl;
for (int i = 0; i < line_num_of_vertex; i++)
{
cout << m_point_array[i] << endl;
}
}
// parse the cin to the geometry
void Line_ND::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != line_num_of_vertex)
{
throw runtime_error("Line_ND::parse_geometry(): wrong vertex number");
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Point_ND point(m_dim);
ss >> point;
m_point_array[i] = point;
}
}
int main()
{
vector<Geometry_ND *> geo_ptr_array;
try
{
string input;
unsigned dim;
Geometry_ND *geo_ptr;
// read dimension
getline(cin, input);
dim = stoi(input);
// read geometry
while (getline(cin, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_ND(dim);
break;
case 'p':
geo_ptr = new Polygon_ND(dim);
break;
case 'l':
geo_ptr = new Line_ND(dim);
break;
default:
throw runtime_error("main(): wrong geometry type");
}
if (input == "t" || input == "p" || input == "l")
{
// parse the cin to the geometry
geo_ptr->parse_geometry(cin);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else
{
throw runtime_error("main(): wrong geometry type");
}
}
// print the geometry
// first, print the dimension
cout << geo_ptr_array[0]->get_geometry_array().at(0).get_dim() << endl;
// second, print the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->print_geometry();
}
}
catch (exception &e)
{
cout << e.what() << endl;
}
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
return 0;
}
Final-2: Save Geometry Objects to Binary File (35%)
-
Inputs:
- Read geometry objects from a input file.
- Please use
int main(int argc, char *argv[])to open the input file (Ref: One and the only: main function. - The file path of the input file is given as
argv[1].
- Please use
- Read the dimensions (
dim) of the coordinate system. The dimension is anunsignedbetween 2 and 10. - Read the type of geometry object in
charformat with the following types:lfor linetfor trianglepfor polygon
- Read the number of vertices in
unsignedformat for each type of geometry object as shown above.- line: 2
- triangle: 3
- polygon: \(n \in Z^+, n \ge 3\)
- Read the vertices with
dimcoordinates indoubleformat.- line:
<double 1><double 2>...<double dim><double 1><double 2>...<double dim> - triangle:
<double 1><double 2>...<double dim><double 1><double 2>...<double dim><double 1><double 2>...<double dim> - polygon:
<double 1><double 2>...<double dim><double 1><double 2>...<double dim>...
- line:
- Read geometry objects from a input file.
-
Outputs:
- Write geometry objects to a output file.
- Please use
int main(int argc, char *argv[])to open the input file (Ref: One and the only: main function. - The file path of the output file is given as
argv[2].
- Please use
- Write the dimensions of the coordinate system.
- Write all geometric objects in the input, with the following information:
- Write the type of the object, the number of vertices, and the vertices.
- The format shold follow the descriptions in Format.
- The order of the vertices and coordinates should be the same as the input.
- Each coordinate should be saved with
doubleformat.
- Write the type of the object, the number of vertices, and the vertices.
- Write the dimension and all geometric objects after the input is finished, and exit the program.
- Write geometry objects to a output file.
-
File name:
final-2_<student_id>.cpp(e.g.final-2_106062802.cpp) -
The program will not have any user prompts, only print the result.
-
The program does not need to handle invalid inputs.
-
The program should base on the
main&print_output_filefunction provided in the pseudo code. -
The program should be finished within 10 seconds. Any test cases will garuntee the program is finished within 10 seconds.
Format
Input/Output File
<dim><geometry type><n><double 1><double 2>...<double dim><double 1><double 2>...<double dim>...<EOF>
Example
Note: For any # started lines are comments for human-readability. The .bin files do not have comments.
dim = 2
Triangle
Input File: input_triangle_2d.bin
# 2
# t
# 3
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# 5.000000000000000,0.000000000000000
# Hex dump
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00
Output File: output_triangle_2d.bin
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00
Terminal:
$ ./a.out input_triangle_2d.bin output_triangle_2d.bin
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00
$
Line
Input File: input_line_2d.bin
# 2
# l
# 2
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# Hex dump
02 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40
Output File: output_line_2d.bin
02 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40
Terminal:
$ ./a.out input_line_2d.bin output_line_2d.bin
02 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40
$
Polygon
Input File: input_polygon_2d.bin
# 2
# p
# 5
# 1.000000000000000,0.000000000000000
# 2.000000000000000,1.100000000000000
# -3.000000000000000,-2.200000000000000
# 4.300000000000000,2.100000000000000
# -1.200000000000000,3.400000000000000
# Hex dump
02 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
40 9a 99 99 99 99 99 f1 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 33 33 33 33 33 33 11
40 cd cc cc cc cc cc 00 40 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40
Output File: output_polygon_2d.bin
02 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
40 9a 99 99 99 99 99 f1 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 33 33 33 33 33 33 11
40 cd cc cc cc cc cc 00 40 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40
Terminal:
$ ./a.out input_polygon_2d.bin output_polygon_2d.bin
02 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
40 9a 99 99 99 99 99 f1 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 33 33 33 33 33 33 11
40 cd cc cc cc cc cc 00 40 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40
$
Multiple Objects
Input File: input_multiple_objects_2d.bin
# 2
# t
# 3
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# 5.000000000000000,0.000000000000000
# l
# 2
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# p
# 5
# 1.000000000000000,0.000000000000000
# 2.000000000000000,1.100000000000000
# -3.000000000000000,-2.200000000000000
# 4.300000000000000,2.100000000000000
# -1.200000000000000,3.400000000000000
# Hex dump
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 6c 02 00 00 00 00 00
00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 70 05
00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99 99
99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33 33
33 0b 40
Output File: output_multiple_objects_2d.bin
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 6c 02 00 00 00 00 00
00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 70 05
00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99 99
99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33 33
33 0b 40
Terminal:
$ ./a.out input_multiple_2d.bin output_multiple_2d.bin
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 6c 02 00 00 00 00 00
00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 70 05
00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99 99
99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33 33
33 0b 40
$
dim = 3
Triangle
Input File: input_triangle_3d.bin
# 3
# t
# 3
# 1.000000000000000,2.000000000000000,3.000000000000000
# 3.000000000000000,4.000000000000000,5.000000000000000
# 5.000000000000000,0.000000000000000,1.000000000000000
# Hex dump
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f
Output File: output_triangle_3d.bin
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f
Terminal:
$ ./a.out input_triangle_3d.bin output_triangle_3d.bin
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f
$
Line
Input File: input_line_3d.bin
# 3
# l
# 2
# 1.000000000000000,2.000000000000000,3.000000000000000
# 3.000000000000000,4.000000000000000,5.000000000000000
# Hex dump
03 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40
Output File: output_line_3d.bin
03 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40
Terminal:
$ ./a.out input_line_3d.bin output_line_3d.bin
03 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40
$
Polygon
Input File: input_polygon_3d.bin
# 3
# p
# 5
# 1.000000000000000,0.000000000000000,-1.000000000000000
# 2.000000000000000,1.100000000000000,0.200000000000000
# -3.000000000000000,-2.200000000000000,-1.300000000000000
# 4.300000000000000,2.100000000000000,0.100000000000000
# -1.200000000000000,3.400000000000000,-5.600000000000000
# Hex dump
03 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
bf 00 00 00 00 00 00 00 40 9a 99 99 99 99 99 f1
3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc cc f4
bf 33 33 33 33 33 33 11 40 cd cc cc cc cc cc 00
40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40 66 66 66 66 66 66 16
c0
Output File: output_polygon_3d.bin
03 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
bf 00 00 00 00 00 00 00 40 9a 99 99 99 99 99 f1
3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc cc f4
bf 33 33 33 33 33 33 11 40 cd cc cc cc cc cc 00
40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40 66 66 66 66 66 66 16
c0
Terminal:
$ ./a.out input_polygon_3d.bin output_polygon_3d.bin
03 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
bf 00 00 00 00 00 00 00 40 9a 99 99 99 99 99 f1
3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc cc f4
bf 33 33 33 33 33 33 11 40 cd cc cc cc cc cc 00
40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40 66 66 66 66 66 66 16
c0
$
Multiple Objects
Input File: input_multiple_objects_3d.bin
# 3
# t
# 3
# 1.000000000000000,2.000000000000000,3.000000000000000
# 3.000000000000000,4.000000000000000,5.000000000000000
# 5.000000000000000,0.000000000000000,1.000000000000000
# l
# 2
# 1.000000000000000,2.000000000000000,3.000000000000000
# 3.000000000000000,4.000000000000000,5.000000000000000
# p
# 5
# 1.000000000000000,0.000000000000000,-1.000000000000000
# 2.000000000000000,1.100000000000000,0.200000000000000
# -3.000000000000000,-2.200000000000000,-1.300000000000000
# 4.300000000000000,2.100000000000000,0.100000000000000
# -1.200000000000000,3.400000000000000,-5.600000000000000
# Hex dump
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f 6c 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00
00 00 00 00 00 40 00 00 00 00 00 00 08 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 14 40 70 05 00 00 00 00 00 00 00 00
00 f0 3f 00 00 00 00 00 00 00 00 00 00 00 00 00
00 f0 bf 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00
00 08 c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc
cc f4 bf 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33
33 f3 bf 33 33 33 33 33 33 0b 40 66 66 66 66 66
66 16 c0
Output File: output_multiple_objects_3d.bin
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f 6c 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00
00 00 00 00 00 40 00 00 00 00 00 00 08 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 14 40 70 05 00 00 00 00 00 00 00 00
00 f0 3f 00 00 00 00 00 00 00 00 00 00 00 00 00
00 f0 bf 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00
00 08 c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc
cc f4 bf 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33
33 f3 bf 33 33 33 33 33 33 0b 40 66 66 66 66 66
66 16 c0
Terminal:
$ ./a.out input_multiple_3d.bin output_multiple_3d.bin
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f 6c 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00
00 00 00 00 00 40 00 00 00 00 00 00 08 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 14 40 70 05 00 00 00 00 00 00 00 00
00 f0 3f 00 00 00 00 00 00 00 00 00 00 00 00 00
00 f0 bf 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00
00 08 c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc
cc f4 bf 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33
33 f3 bf 33 33 33 33 33 33 0b 40 66 66 66 66 66
66 16 c0
$
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <fstream>
#include <vector>
#include <exception>
#include <iomanip>
using namespace std;
class Geometry_ND;
class Point_ND
{
private:
vector<double> m_coords;
unsigned m_dim;
friend class Geometry_ND;
public:
// Constructor, initializes dimension and coordinates
Point_ND(const unsigned &arg_dim = 2);
// Copy constructor
Point_ND(const Point_ND &arg_point);
// assignment operator
Point_ND &operator=(const Point_ND &arg_point);
// get coordinates
vector<double> get_coords() const;
// get dimension
unsigned get_dim() const;
// set coordinates
void set_coords(const vector<double> &arg_coords);
// write data members in binary format
void write_binary_coords(ofstream &arg_ofs);
// read data members in binary format
void read_binary_coords(ifstream &arg_ifs);
// friend class
friend class Geometry_ND;
};
class Geometry_ND
{
protected:
// data members
vector<Point_ND> m_point_array;
unsigned m_dim;
public:
// Constructor, initializes the array
Geometry_ND(const unsigned &arg_dim = 2,
const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_ND(const Geometry_ND &arg_geometry);
// assignment operator
Geometry_ND &operator=(const Geometry_ND &arg_geometry);
// print the geometry
virtual void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
virtual void parse_geometry(ifstream &arg_ifs);
// set the geometry
void set_geometry(const vector<Point_ND> &arg_point_array);
// get the geometry array
vector<Point_ND> get_geometry_array();
};
class Triangle_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Triangle_ND(const unsigned &arg_dim = 2);
// Copy constructor
Triangle_ND(const Triangle_ND &arg_triangle);
// assignment operator
Triangle_ND &operator=(const Triangle_ND &arg_triangle);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned triangle_num_of_vertex = 3;
class Polygon_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Polygon_ND(const unsigned &arg_dim = 2);
// Copy constructor
Polygon_ND(const Polygon_ND &arg_polygon);
// assignment operator
Polygon_ND &operator=(const Polygon_ND &arg_polygon);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
class Line_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Line_ND(const unsigned &arg_dim = 2);
// Copy constructor
Line_ND(const Line_ND &arg_line);
// assignment operator
Line_ND &operator=(const Line_ND &arg_line);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned line_num_of_vertex = 2;
// Ref: https://stackoverflow.com/q/9621893
void print_output_file(int argc, char *argv[])
{
ifstream ans_ifs(argv[2], ios::in | ios::binary);
if (!ans_ifs)
{
cout << "Error: Cannot open output file" << endl;
exit(1);
}
char ans_block = 0;
unsigned offset_count = 0;
ans_ifs.read(&ans_block, 1);
while (!ans_ifs.eof())
{
int z = ans_block & 0xff;
cout << std::hex
<< std::setfill('0')
<< std::setw(2)
<< z
<< " ";
offset_count++;
if (offset_count % 16 == 0)
{
cout << endl;
}
ans_ifs.read(&ans_block, 1);
}
cout << endl;
ans_ifs.close();
}
int main(int argc, char *argv[])
{
vector<Geometry_ND *> geo_ptr_array;
string input_file_path(argv[1]);
string output_file_path(argv[2]);
char input;
unsigned dim;
Geometry_ND *geo_ptr;
// open the input file
ifstream infile(input_file_path, ios::in | ios::binary);
// open the output file
ofstream outfile(output_file_path, ios::out | ios::trunc | ios::binary);
// read dimension
// read geometry
while (infile.get(input))
{
// check the geometry type
switch (input)
{
case 't':
geo_ptr = new Triangle_ND(dim);
break;
case 'p':
geo_ptr = new Polygon_ND(dim);
break;
case 'l':
geo_ptr = new Line_ND(dim);
break;
}
if (input == 't' || input == 'p' || input == 'l')
{
// parse the infile to the geometry
geo_ptr->parse_geometry(infile);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
}
// print the geometry
// first, print the dimension
// second, print the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->print_geometry(outfile);
}
// close the input & output file
infile.close();
outfile.close();
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
print_output_file(argc, argv);
return 0;
}
Reference Code:
TA
#include <iostream>
#include <string>
#include <sstream>
#include <fstream>
#include <vector>
#include <exception>
#include <iomanip>
using namespace std;
class Geometry_ND;
class Point_ND
{
private:
vector<double> m_coords;
unsigned m_dim;
friend class Geometry_ND;
public:
// Constructor, initializes the array
Point_ND(const unsigned &arg_dim = 2);
// Copy constructor
Point_ND(const Point_ND &arg_point);
// assignment operator
Point_ND &operator=(const Point_ND &arg_point);
// get coordinates
vector<double> get_coords() const;
// get dimension
unsigned get_dim() const;
// set coordinates
void set_coords(const vector<double> &arg_coords);
// write data members in binary format
void write_binary_coords(ofstream &arg_ofs);
// read data members in binary format
void read_binary_coords(ifstream &arg_ifs);
// friend class
friend class Geometry_ND;
};
class Geometry_ND
{
protected:
// data members
vector<Point_ND> m_point_array;
unsigned m_dim;
public:
// Constructor, initializes the array
Geometry_ND(const unsigned &arg_dim = 2,
const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_ND(const Geometry_ND &arg_geometry);
// assignment operator
Geometry_ND &operator=(const Geometry_ND &arg_geometry);
// print the geometry
virtual void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
virtual void parse_geometry(ifstream &arg_ifs);
// set the geometry
void set_geometry(const vector<Point_ND> &arg_point_array);
// get the geometry array
vector<Point_ND> get_geometry_array();
};
class Triangle_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Triangle_ND(const unsigned &arg_dim = 2);
// Copy constructor
Triangle_ND(const Triangle_ND &arg_triangle);
// assignment operator
Triangle_ND &operator=(const Triangle_ND &arg_triangle);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned triangle_num_of_vertex = 3;
class Polygon_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Polygon_ND(const unsigned &arg_dim = 2);
// Copy constructor
Polygon_ND(const Polygon_ND &arg_polygon);
// assignment operator
Polygon_ND &operator=(const Polygon_ND &arg_polygon);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
class Line_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Line_ND(const unsigned &arg_dim = 2);
// Copy constructor
Line_ND(const Line_ND &arg_line);
// assignment operator
Line_ND &operator=(const Line_ND &arg_line);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned line_num_of_vertex = 2;
// Ref: https://stackoverflow.com/q/9621893
void print_output_file(int argc, char *argv[])
{
ifstream ans_ifs(argv[2], ios::in | ios::binary);
if (!ans_ifs)
{
cout << "Error: Cannot open output file" << endl;
exit(1);
}
char ans_block = 0;
unsigned offset_count = 0;
ans_ifs.read(&ans_block, 1);
while (!ans_ifs.eof())
{
int z = ans_block & 0xff;
cout << std::hex
<< std::setfill('0')
<< std::setw(2)
<< z
<< " ";
offset_count++;
if (offset_count % 16 == 0)
{
cout << endl;
}
ans_ifs.read(&ans_block, 1);
}
cout << endl;
ans_ifs.close();
}
// Point_ND class implementation
// Constructor
Point_ND::Point_ND(const unsigned &arg_dim)
: m_dim(arg_dim), m_coords(arg_dim)
{
}
// Copy constructor
Point_ND::Point_ND(const Point_ND &arg_point)
: m_dim(arg_point.m_dim), m_coords(arg_point.m_coords)
{
}
// assignment operator
Point_ND &Point_ND::operator=(const Point_ND &arg_point)
{
if (this != &arg_point)
{
m_dim = arg_point.m_dim;
m_coords = arg_point.m_coords;
}
return *this;
}
// get dimension
unsigned Point_ND::get_dim() const
{
return m_dim;
}
// get coordinates
vector<double> Point_ND::get_coords() const
{
return m_coords;
}
// set coordinates
void Point_ND::set_coords(const vector<double> &arg_coords)
{
m_coords = arg_coords;
}
// write data members in binary format
void Point_ND::write_binary_coords(ofstream &arg_ofs)
{
for (unsigned i = 0; i < m_dim; i++)
{
arg_ofs.write((char *)&m_coords[i], sizeof(double));
}
}
// read data members in binary format
void Point_ND::read_binary_coords(ifstream &arg_ifs)
{
double temp_double;
for (unsigned i = 0; i < m_dim; i++)
{
arg_ifs.read((char *)&temp_double, sizeof(double));
m_coords[i] = temp_double;
}
}
// Geometry_ND class implementation
// Constructor, initializes the array
Geometry_ND::Geometry_ND(const unsigned &arg_dim, const unsigned int &arg_num_of_vertex)
: m_dim(arg_dim), m_point_array(arg_num_of_vertex)
{
}
// Copy constructor
Geometry_ND::Geometry_ND(const Geometry_ND &arg_geometry)
: m_dim(arg_geometry.m_dim), m_point_array(arg_geometry.m_point_array)
{
}
// assignment operator
Geometry_ND &Geometry_ND::operator=(const Geometry_ND &arg_geometry)
{
if (this == &arg_geometry) // self-assignment
return *this;
m_point_array = arg_geometry.m_point_array;
return *this;
}
// print the geometry
void Geometry_ND::print_geometry(ofstream &arg_ofs)
{
throw runtime_error("print_geometry() is not implemented");
}
// parse the cin to the geometry
void Geometry_ND::parse_geometry(ifstream &arg_ifs)
{
throw runtime_error("parse_geometry() is not implemented");
}
// set the geometry
void Geometry_ND::set_geometry(const vector<Point_ND> &arg_point_array)
{
// check the dimension
for (unsigned i = 0; i < arg_point_array.size(); i++)
{
if (arg_point_array[i].get_dim() != m_dim)
{
throw runtime_error("The dimension of the geometry is not consistent");
}
}
m_point_array = arg_point_array;
}
// get the geometry array
vector<Point_ND> Geometry_ND::get_geometry_array()
{
return m_point_array;
}
// Triangle_ND class implementation
// Constructor, initializes the array
Triangle_ND::Triangle_ND(const unsigned &arg_dim)
: Geometry_ND(arg_dim, triangle_num_of_vertex)
{
}
// Copy constructor
Triangle_ND::Triangle_ND(const Triangle_ND &arg_triangle)
: Geometry_ND(arg_triangle)
{
}
// assignment operator
Triangle_ND &Triangle_ND::operator=(const Triangle_ND &arg_triangle)
{
if (this == &arg_triangle) // self-assignment
return *this;
Geometry_ND::operator=(arg_triangle);
return *this;
}
// print the geometry
void Triangle_ND::print_geometry(ofstream &arg_ofs)
{
unsigned num_of_vertex = m_point_array.size();
arg_ofs.write("t", 1);
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (int i = 0; i < num_of_vertex; i++)
{
m_point_array[i].write_binary_coords(arg_ofs);
}
}
// parse the cin to the geometry
void Triangle_ND::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num != triangle_num_of_vertex)
{
throw runtime_error("Triangle_ND::parse_geometry(): wrong vertex number");
}
for (int i = 0; i < vertex_num; i++)
{
Point_ND point(m_dim);
point.read_binary_coords(arg_ifs);
m_point_array[i] = point;
}
}
// Polygon_ND class implementation
// Constructor, initializes the array
Polygon_ND::Polygon_ND(const unsigned &arg_dim)
: Geometry_ND(arg_dim)
{
}
// Copy constructor
Polygon_ND::Polygon_ND(const Polygon_ND &arg_polygon)
: Geometry_ND(arg_polygon)
{
}
// assignment operator
Polygon_ND &Polygon_ND::operator=(const Polygon_ND &arg_polygon)
{
if (this == &arg_polygon) // self-assignment
return *this;
Geometry_ND::operator=(arg_polygon);
return *this;
}
// print the geometry
void Polygon_ND::print_geometry(ofstream &arg_ofs)
{
unsigned num_of_vertex = m_point_array.size();
arg_ofs.write("p", 1);
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (int i = 0; i < num_of_vertex; i++)
{
m_point_array[i].write_binary_coords(arg_ofs);
}
}
// parse the cin to the geometry
void Polygon_ND::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num < 3)
{
throw runtime_error("Polygon_ND::parse_geometry(): wrong vertex number");
}
m_point_array.resize(vertex_num);
for (int i = 0; i < vertex_num; i++)
{
Point_ND point(m_dim);
point.read_binary_coords(arg_ifs);
m_point_array[i] = point;
}
}
// Line_ND class implementation
// Constructor, initializes the array
Line_ND::Line_ND(const unsigned &arg_dim)
: Geometry_ND(arg_dim, line_num_of_vertex)
{
}
// Copy constructor
Line_ND::Line_ND(const Line_ND &arg_line)
: Geometry_ND(arg_line)
{
}
// assignment operator
Line_ND &Line_ND::operator=(const Line_ND &arg_line)
{
if (this == &arg_line) // self-assignment
return *this;
Geometry_ND::operator=(arg_line);
return *this;
}
// print the geometry
void Line_ND::print_geometry(ofstream &arg_ofs)
{
unsigned num_of_vertex = m_point_array.size();
arg_ofs.write("l", 1);
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (int i = 0; i < num_of_vertex; i++)
{
m_point_array[i].write_binary_coords(arg_ofs);
}
}
// parse the cin to the geometry
void Line_ND::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num != line_num_of_vertex)
{
throw runtime_error("Line_ND::parse_geometry(): wrong vertex number");
}
for (int i = 0; i < vertex_num; i++)
{
Point_ND point(m_dim);
point.read_binary_coords(arg_ifs);
m_point_array[i] = point;
}
}
int main(int argc, char *argv[])
{
vector<Geometry_ND *> geo_ptr_array;
string input_file_path(argv[1]);
string output_file_path(argv[2]);
try
{
char input;
unsigned dim;
Geometry_ND *geo_ptr;
// open the input file
ifstream infile(input_file_path, ios::in | ios::binary);
infile.exceptions(ios::badbit);
// open the output file
ofstream outfile(output_file_path, ios::out | ios::trunc | ios::binary);
outfile.exceptions(ios::badbit);
// read dimension
infile.read((char *)&dim, sizeof(unsigned));
if (dim < 2 || dim > 10)
{
throw runtime_error("main(): wrong dimension");
}
// read geometry
while (infile.get(input))
{
// check the geometry type
switch (input)
{
case 't':
geo_ptr = new Triangle_ND(dim);
break;
case 'p':
geo_ptr = new Polygon_ND(dim);
break;
case 'l':
geo_ptr = new Line_ND(dim);
break;
default:
throw runtime_error("main(): wrong geometry type");
}
if (input == 't' || input == 'p' || input == 'l')
{
// change exception mask
infile.exceptions(ios::badbit | ios::failbit | ios::eofbit);
// parse the infile to the geometry
geo_ptr->parse_geometry(infile);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
// rollback the exception mask
infile.exceptions(ios::badbit);
}
else
{
throw runtime_error("main(): wrong geometry type");
}
}
// print the geometry
// first, print the dimension
outfile.write((char *)&dim, sizeof(unsigned));
// second, print the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->print_geometry(outfile);
}
// close the input & output file
infile.close();
outfile.close();
}
catch (exception &e)
{
cout << e.what() << endl;
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
return 1;
}
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
print_output_file(argc, argv);
return 0;
}
Convert Text Version Input to Binary Version Input
/*** convert text version input to binary version input ***/
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>
using namespace std;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
int main(int argc, char *argv[])
{
if (argc != 3)
{
cout << "Usage: txt_to_bin <input_file> <output_file>" << endl;
return 1;
}
ifstream input_file(argv[1]);
ofstream output_file(argv[2], ios::binary | ios::trunc);
if (!input_file.is_open())
{
cout << "Could not open input file" << endl;
return 1;
}
if (!output_file.is_open())
{
cout << "Could not open output file" << endl;
return 1;
}
string line, temp;
unsigned num_of_vertices = 1;
// read dimensions
getline(input_file, line);
unsigned num_of_dimensions = stoul(line);
// write dimensions
output_file.write((char *)&num_of_dimensions, sizeof(unsigned));
while (getline(input_file, line))
{
// check the geometry type
switch (line[0])
{
case 't':
case 'p':
case 'l':
// get the number of vertices from the next line
getline(input_file, temp);
num_of_vertices = stoul(temp);
break;
default:
error_and_exit();
}
// write the geometry type
char geometry_type = line[0];
output_file.write(&geometry_type, 1);
// write the number of vertices
if (line[0] == 't' || line[0] == 'p' || line[0] == 'l')
{
output_file.write((char *)&num_of_vertices, sizeof(unsigned));
}
// convert the lines to binary
for (int i = 0; i < num_of_vertices; i++)
{
getline(input_file, line);
stringstream ss(line);
for (int j = 0; j < num_of_dimensions; j++)
{
getline(ss, temp, ',');
double value = stod(temp);
output_file.write((char *)&value, sizeof(double));
}
}
}
input_file.close();
output_file.close();
return 0;
}
Convert Binary Version Input/Output to Human-readable Input/Output & Dump HEX File
/*** convert binary version input to human-readable input & dump hex file ***/
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>
#include <iomanip>
using namespace std;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
int main(int argc, char *argv[])
{
if (argc != 3)
{
cout << "Usage: bin_to_txt <input_file> <output_file>" << endl;
return 1;
}
ifstream input_file(argv[1], ios::binary);
ofstream output_file(argv[2], ios::trunc);
if (!input_file.is_open())
{
cout << "Could not open input file" << endl;
return 1;
}
if (!output_file.is_open())
{
cout << "Could not open output file" << endl;
return 1;
}
char input;
unsigned num_of_vertices = 1;
// read dimensions
unsigned num_of_dimensions = 2;
input_file.read((char *)&num_of_dimensions, sizeof(unsigned));
// write dimensions
output_file << "# " << num_of_dimensions << endl;
while (input_file.get(input))
{
// check the geometry type
switch (input)
{
case 't':
case 'p':
case 'l':
// get the number of vertices from the next line
input_file.read((char *)&num_of_vertices, sizeof(unsigned));
break;
default:
error_and_exit();
}
// write the geometry type
char geometry_type = input;
output_file << "# " << geometry_type << endl;
// write the number of vertices
if (geometry_type == 't' || geometry_type == 'p' || geometry_type == 'l')
{
output_file << "# " << num_of_vertices << endl;
}
// convert the lines to human-readable format
for (int i = 0; i < num_of_vertices; i++)
{
output_file << "# " << setprecision(15) << fixed;
for (int j = 0; j < num_of_dimensions; j++)
{
double temp;
input_file.read((char *)&temp, sizeof(double));
if (j != 0)
{
output_file << ",";
}
output_file << temp;
}
output_file << endl;
}
}
input_file.close();
input_file.open(argv[1], ios::binary);
output_file << "# Hex dump" << endl;
char file_block = 0;
unsigned offset_count = 0;
input_file.read(&file_block, 1);
while (!input_file.eof())
{
int z = file_block & 0xff;
output_file << std::hex
<< std::setfill('0')
<< std::setw(2)
<< z
<< " ";
offset_count++;
if (offset_count % 16 == 0)
{
output_file << endl;
}
input_file.read(&file_block, 1);
}
output_file << endl;
output_file.close();
return 0;
}
Final-3: Save Geometry Objects to Binary File & Exception Handling (15%)
-
Inputs:
- Read geometry objects from a input file.
- Please use
int main(int argc, char *argv[])to open the input file (Ref: One and the only: main function. - The file path of the input file is given as
argv[1].
- Please use
- Read the dimensions (
dim) of the coordinate system. The dimension is anunsignedbetween 2 and 10. - Read the type of geometry object in
charformat with the following types:lfor linetfor trianglepfor polygon
- Read the number of vertices in
unsignedformat for each type of geometry object as shown above.- line: 2
- triangle: 3
- polygon: \(n \in Z^+, n \ge 3\)
- Read the vertices with
dimcoordinates indoubleformat.- line:
<double 1><double 2>...<double dim><double 1><double 2>...<double dim> - triangle:
<double 1><double 2>...<double dim><double 1><double 2>...<double dim><double 1><double 2>...<double dim> - polygon:
<double 1><double 2>...<double dim><double 1><double 2>...<double dim>...
- line:
- Read geometry objects from a input file.
-
Outputs:
- Write geometry objects to a output file.
- Please use
int main(int argc, char *argv[])to open the input file (Ref: One and the only: main function. - The file path of the output file is given as
argv[2].
- Please use
- Write the dimensions of the coordinate system.
- Write all geometric objects in the input, with the following information:
- Write the type of the object, the number of vertices, and the vertices.
- The format shold follow the descriptions in Format.
- The order of the vertices and coordinates should be the same as the input.
- Each coordinate should be saved with
doubleformat.
- Write the type of the object, the number of vertices, and the vertices.
- Write the dimension and all geometric objects after the input is finished, and exit the program.
- Write geometry objects to a output file.
-
File name:
final-3_<student_id>.cpp(e.g.final-3_106062802.cpp) -
The program will not have any user prompts, only print the result.
-
The program needs to handle the exceptions in Error Handling. Other exceptions will not occur.
-
The program should base on the
main&print_output_filefunction provided in the pseudo code. -
If the input file is invalid, the program should print the error message
Error: Invalid inputin the terminal and terminate the program. -
The program should be finished within 10 seconds. Any test cases will garuntee the program is finished within 10 seconds.
Format
Input/Output File
<dim><geometry type><n><double 1><double 2>...<double dim><double 1><double 2>...<double dim>...<EOF>
Example
Note: For any # started lines are comments for human-readability. The .bin files do not have comments.
dim = 2
Triangle
Input File: input_triangle_2d.bin
# 2
# t
# 3
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# 5.000000000000000,0.000000000000000
# Hex dump
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00
Output File: output_triangle_2d.bin
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00
Terminal:
$ ./a.out input_triangle_2d.bin output_triangle_2d.bin
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00
$
Line
Input File: input_line_2d.bin
# 2
# l
# 2
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# Hex dump
02 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40
Output File: output_line_2d.bin
02 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40
Terminal:
$ ./a.out input_line_2d.bin output_line_2d.bin
02 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40
$
Polygon
Input File: input_polygon_2d.bin
# 2
# p
# 5
# 1.000000000000000,0.000000000000000
# 2.000000000000000,1.100000000000000
# -3.000000000000000,-2.200000000000000
# 4.300000000000000,2.100000000000000
# -1.200000000000000,3.400000000000000
# Hex dump
02 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
40 9a 99 99 99 99 99 f1 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 33 33 33 33 33 33 11
40 cd cc cc cc cc cc 00 40 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40
Output File: output_polygon_2d.bin
02 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
40 9a 99 99 99 99 99 f1 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 33 33 33 33 33 33 11
40 cd cc cc cc cc cc 00 40 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40
Terminal:
$ ./a.out input_polygon_2d.bin output_polygon_2d.bin
02 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
40 9a 99 99 99 99 99 f1 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 33 33 33 33 33 33 11
40 cd cc cc cc cc cc 00 40 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40
$
Multiple Objects
Input File: input_multiple_objects_2d.bin
# 2
# t
# 3
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# 5.000000000000000,0.000000000000000
# l
# 2
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# p
# 5
# 1.000000000000000,0.000000000000000
# 2.000000000000000,1.100000000000000
# -3.000000000000000,-2.200000000000000
# 4.300000000000000,2.100000000000000
# -1.200000000000000,3.400000000000000
# Hex dump
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 6c 02 00 00 00 00 00
00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 70 05
00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99 99
99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33 33
33 0b 40
Output File: output_multiple_objects_2d.bin
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 6c 02 00 00 00 00 00
00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 70 05
00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99 99
99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33 33
33 0b 40
Terminal:
$ ./a.out input_multiple_objects_2d.bin output_multiple_objects_2d.bin
02 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 6c 02 00 00 00 00 00
00 00 00 00 f0 3f 00 00 00 00 00 00 00 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 70 05
00 00 00 00 00 00 00 00 00 f0 3f 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 00 00 00 00 00 00 08 c0 9a 99 99 99 99
99 01 c0 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 33 33 33 33 33 33 f3 bf 33 33 33 33 33
33 0b 40
$
dim = 3
Triangle
Input File: input_triangle_3d.bin
# 3
# t
# 3
# 1.000000000000000,2.000000000000000,3.000000000000000
# 3.000000000000000,4.000000000000000,5.000000000000000
# 5.000000000000000,0.000000000000000,1.000000000000000
# Hex dump
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f
Output File: output_triangle_3d.bin
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f
Terminal:
$ ./a.out input_triangle_3d.bin output_triangle_3d.bin
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f
$
Line
Input File: input_line_3d.bin
# 3
# l
# 2
# 1.000000000000000,2.000000000000000,3.000000000000000
# 3.000000000000000,4.000000000000000,5.000000000000000
# Hex dump
03 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40
Output File: output_line_3d.bin
03 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40
Terminal:
$ ./a.out input_line_3d.bin output_line_3d.bin
03 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40
$
Polygon
Input File: input_polygon_3d.bin
# 3
# p
# 5
# 1.000000000000000,0.000000000000000,-1.000000000000000
# 2.000000000000000,1.100000000000000,0.200000000000000
# -3.000000000000000,-2.200000000000000,-1.300000000000000
# 4.300000000000000,2.100000000000000,0.100000000000000
# -1.200000000000000,3.400000000000000,-5.600000000000000
# Hex dump
03 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
bf 00 00 00 00 00 00 00 40 9a 99 99 99 99 99 f1
3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc cc f4
bf 33 33 33 33 33 33 11 40 cd cc cc cc cc cc 00
40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40 66 66 66 66 66 66 16
c0
Output File: output_polygon_3d.bin
03 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
bf 00 00 00 00 00 00 00 40 9a 99 99 99 99 99 f1
3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc cc f4
bf 33 33 33 33 33 33 11 40 cd cc cc cc cc cc 00
40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40 66 66 66 66 66 66 16
c0
Terminal:
$ ./a.out input_polygon_3d.bin output_polygon_3d.bin
03 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
bf 00 00 00 00 00 00 00 40 9a 99 99 99 99 99 f1
3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc cc f4
bf 33 33 33 33 33 33 11 40 cd cc cc cc cc cc 00
40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40 66 66 66 66 66 66 16
c0
$
Multiple Objects
Input File: input_multiple_objects_3d.bin
# 3
# t
# 3
# 1.000000000000000,2.000000000000000,3.000000000000000
# 3.000000000000000,4.000000000000000,5.000000000000000
# 5.000000000000000,0.000000000000000,1.000000000000000
# l
# 2
# 1.000000000000000,2.000000000000000,3.000000000000000
# 3.000000000000000,4.000000000000000,5.000000000000000
# p
# 5
# 1.000000000000000,0.000000000000000,-1.000000000000000
# 2.000000000000000,1.100000000000000,0.200000000000000
# -3.000000000000000,-2.200000000000000,-1.300000000000000
# 4.300000000000000,2.100000000000000,0.100000000000000
# -1.200000000000000,3.400000000000000,-5.600000000000000
# Hex dump
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f 6c 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00
00 00 00 00 00 40 00 00 00 00 00 00 08 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 14 40 70 05 00 00 00 00 00 00 00 00
00 f0 3f 00 00 00 00 00 00 00 00 00 00 00 00 00
00 f0 bf 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00
00 08 c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc
cc f4 bf 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33
33 f3 bf 33 33 33 33 33 33 0b 40 66 66 66 66 66
66 16 c0
Output File: output_multiple_objects_3d.bin
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f 6c 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00
00 00 00 00 00 40 00 00 00 00 00 00 08 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 14 40 70 05 00 00 00 00 00 00 00 00
00 f0 3f 00 00 00 00 00 00 00 00 00 00 00 00 00
00 f0 bf 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00
00 08 c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc
cc f4 bf 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33
33 f3 bf 33 33 33 33 33 33 0b 40 66 66 66 66 66
66 16 c0
Terminal:
$ ./a.out input_multiple_objects_3d.bin output_multiple_objects_3d.bin
03 00 00 00 74 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f 6c 02 00 00 00 00 00 00 00 00 00 f0 3f 00 00
00 00 00 00 00 40 00 00 00 00 00 00 08 40 00 00
00 00 00 00 08 40 00 00 00 00 00 00 10 40 00 00
00 00 00 00 14 40 70 05 00 00 00 00 00 00 00 00
00 f0 3f 00 00 00 00 00 00 00 00 00 00 00 00 00
00 f0 bf 00 00 00 00 00 00 00 40 9a 99 99 99 99
99 f1 3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00
00 08 c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc
cc f4 bf 33 33 33 33 33 33 11 40 cd cc cc cc cc
cc 00 40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33
33 f3 bf 33 33 33 33 33 33 0b 40 66 66 66 66 66
66 16 c0
$
Error Handling
Wrong dimensions
Input File: input_wrong_dim.bin
# 11
# l
# 2
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# Hex dump
0b 00 00 00 6c 02 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40
Output File: output_wrong_dim.bin
Terminal:
$ ./a.out input_wrong_dim.bin output_wrong_dim.bin
Error: Invalid input
$
Wrong type of object
Input File: input_wrong_type.bin
# 3
# u
# 3
# 1.000000000000000,2.000000000000000,3.000000000000000
# 3.000000000000000,4.000000000000000,5.000000000000000
# 5.000000000000000,0.000000000000000,1.000000000000000
# Hex dump
03 00 00 00 75 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 08 40 00 00 00 00 00 00 10
40 00 00 00 00 00 00 14 40 00 00 00 00 00 00 14
40 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
3f
Output File: output_wrong_type.bin
Terminal:
$ ./a.out input_wrong_type.bin output_wrong_type.bin
Error: Invalid input
$
Wrong number of vertices
Case 1
Input File: input_wrong_line_vtx.bin
# 2
# l
# 3
# 1.000000000000000,2.000000000000000
# 3.000000000000000,4.000000000000000
# Hex dump
02 00 00 00 6c 03 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 40 00 00 00 00 00 00 08
40 00 00 00 00 00 00 10 40
Output File: output_wrong_line_vtx.bin
Terminal:
$ ./a.out input_wrong_line_vtx.bin output_wrong_line_vtx.bin
Error: Invalid input
$
Case 2
Input File: input_wrong_polygon_vtx.bin
# 3
# p
# 2
# 1.000000000000000,0.000000000000000,-1.000000000000000
# 2.000000000000000,1.100000000000000,0.200000000000000
# -3.000000000000000,-2.200000000000000,-1.300000000000000
# 4.300000000000000,2.100000000000000,0.100000000000000
# -1.200000000000000,3.400000000000000,-5.600000000000000
# Hex dump
03 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f0
bf 00 00 00 00 00 00 00 40 9a 99 99 99 99 99 f1
3f 9a 99 99 99 99 99 c9 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 cd cc cc cc cc cc f4
bf 33 33 33 33 33 33 11 40 cd cc cc cc cc cc 00
40 9a 99 99 99 99 99 b9 3f 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40 66 66 66 66 66 66 16
c0
Output File: output_wrong_polygon_vtx.bin
Terminal:
$ ./a.out input_wrong_polygon_vtx.bin output_wrong_polygon_vtx.bin
Error: Invalid input
$
Wrong vertex coordinates/vertex amount
Input File: input_wrong_vtx_amount.bin
# 3
# p
# 5
# 1.000000000000000,0.000000000000000
# 2.000000000000000,1.100000000000000
# -3.000000000000000,-2.200000000000000
# 4.300000000000000,2.100000000000000
# -1.200000000000000,3.400000000000000
# Hex dump
02 00 00 00 70 05 00 00 00 00 00 00 00 00 00 f0
3f 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
40 9a 99 99 99 99 99 f1 3f 00 00 00 00 00 00 08
c0 9a 99 99 99 99 99 01 c0 33 33 33 33 33 33 11
40 cd cc cc cc cc cc 00 40 33 33 33 33 33 33 f3
bf 33 33 33 33 33 33 0b 40
Output File: output_wrong_vtx_amount.bin
Terminal:
$ ./a.out input_wrong_vtx_amount.bin output_wrong_vtx_amount.bin
Error: Invalid input
$
Pseudo Code
#include <iostream>
#include <string>
#include <sstream>
#include <fstream>
#include <vector>
#include <exception>
#include <iomanip>
using namespace std;
class Geometry_ND;
class Point_ND
{
private:
vector<double> m_coords;
unsigned m_dim;
friend class Geometry_ND;
public:
// Constructor, initializes dimension and coordinates
Point_ND(const unsigned &arg_dim = 2);
// Copy constructor
Point_ND(const Point_ND &arg_point);
// assignment operator
Point_ND &operator=(const Point_ND &arg_point);
// get coordinates
vector<double> get_coords() const;
// get dimension
unsigned get_dim() const;
// set coordinates
void set_coords(const vector<double> &arg_coords);
// write data members in binary format
void write_binary_coords(ofstream &arg_ofs);
// read data members in binary format
void read_binary_coords(ifstream &arg_ifs);
// friend class
friend class Geometry_ND;
};
class Geometry_ND
{
protected:
// data members
vector<Point_ND> m_point_array;
unsigned m_dim;
public:
// Constructor, initializes the array
Geometry_ND(const unsigned &arg_dim = 2,
const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_ND(const Geometry_ND &arg_geometry);
// assignment operator
Geometry_ND &operator=(const Geometry_ND &arg_geometry);
// print the geometry
virtual void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
virtual void parse_geometry(ifstream &arg_ifs);
// set the geometry
void set_geometry(const vector<Point_ND> &arg_point_array);
// get the geometry array
vector<Point_ND> get_geometry_array();
};
class Triangle_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Triangle_ND(const unsigned &arg_dim = 2);
// Copy constructor
Triangle_ND(const Triangle_ND &arg_triangle);
// assignment operator
Triangle_ND &operator=(const Triangle_ND &arg_triangle);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned triangle_num_of_vertex = 3;
class Polygon_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Polygon_ND(const unsigned &arg_dim = 2);
// Copy constructor
Polygon_ND(const Polygon_ND &arg_polygon);
// assignment operator
Polygon_ND &operator=(const Polygon_ND &arg_polygon);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
class Line_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Line_ND(const unsigned &arg_dim = 2);
// Copy constructor
Line_ND(const Line_ND &arg_line);
// assignment operator
Line_ND &operator=(const Line_ND &arg_line);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned line_num_of_vertex = 2;
// Ref: https://stackoverflow.com/q/9621893
void print_output_file(int argc, char *argv[])
{
ifstream ans_ifs(argv[2], ios::in | ios::binary);
if (!ans_ifs)
{
cout << "Error: Cannot open output file" << endl;
exit(1);
}
char ans_block = 0;
unsigned offset_count = 0;
ans_ifs.read(&ans_block, 1);
while (!ans_ifs.eof())
{
int z = ans_block & 0xff;
cout << std::hex
<< std::setfill('0')
<< std::setw(2)
<< z
<< " ";
offset_count++;
if (offset_count % 16 == 0)
{
cout << endl;
}
ans_ifs.read(&ans_block, 1);
}
cout << endl;
ans_ifs.close();
}
int main(int argc, char *argv[])
{
vector<Geometry_ND *> geo_ptr_array;
string input_file_path(argv[1]);
string output_file_path(argv[2]);
// run codes with exception handling
{
char input;
unsigned dim;
Geometry_ND *geo_ptr;
// open the input file
ifstream infile(input_file_path, ios::in | ios::binary);
// open the output file
ofstream outfile(output_file_path, ios::out | ios::trunc | ios::binary);
// read dimension
infile.read((char *)&dim, sizeof(unsigned));
if ()
{
}
// read geometry
while (infile.get(input))
{
// check the geometry type
switch (input)
{
case 't':
geo_ptr = new Triangle_ND(dim);
break;
case 'p':
geo_ptr = new Polygon_ND(dim);
break;
case 'l':
geo_ptr = new Line_ND(dim);
break;
default:
}
if (input == 't' || input == 'p' || input == 'l')
{
// parse the infile to the geometry
geo_ptr->parse_geometry(infile);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else
{
}
}
// print the geometry
// first, print the dimension
// second, print the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->print_geometry(outfile);
}
// close the input & output file
infile.close();
outfile.close();
}
// catch the exception
{
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
return 1;
}
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
print_output_file(argc, argv);
return 0;
}
Reference Code:
TA
#include <iostream>
#include <string>
#include <sstream>
#include <fstream>
#include <vector>
#include <exception>
#include <iomanip>
using namespace std;
class Geometry_ND;
class Point_ND
{
private:
vector<double> m_coords;
unsigned m_dim;
friend class Geometry_ND;
public:
// Constructor, initializes the array
Point_ND(const unsigned &arg_dim = 2);
// Copy constructor
Point_ND(const Point_ND &arg_point);
// assignment operator
Point_ND &operator=(const Point_ND &arg_point);
// get coordinates
vector<double> get_coords() const;
// get dimension
unsigned get_dim() const;
// set coordinates
void set_coords(const vector<double> &arg_coords);
// write data members in binary format
void write_binary_coords(ofstream &arg_ofs);
// read data members in binary format
void read_binary_coords(ifstream &arg_ifs);
// friend class
friend class Geometry_ND;
};
class Geometry_ND
{
protected:
// data members
vector<Point_ND> m_point_array;
unsigned m_dim;
public:
// Constructor, initializes the array
Geometry_ND(const unsigned &arg_dim = 2,
const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_ND(const Geometry_ND &arg_geometry);
// assignment operator
Geometry_ND &operator=(const Geometry_ND &arg_geometry);
// print the geometry
virtual void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
virtual void parse_geometry(ifstream &arg_ifs);
// set the geometry
void set_geometry(const vector<Point_ND> &arg_point_array);
// get the geometry array
vector<Point_ND> get_geometry_array();
};
class Triangle_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Triangle_ND(const unsigned &arg_dim = 2);
// Copy constructor
Triangle_ND(const Triangle_ND &arg_triangle);
// assignment operator
Triangle_ND &operator=(const Triangle_ND &arg_triangle);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned triangle_num_of_vertex = 3;
class Polygon_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Polygon_ND(const unsigned &arg_dim = 2);
// Copy constructor
Polygon_ND(const Polygon_ND &arg_polygon);
// assignment operator
Polygon_ND &operator=(const Polygon_ND &arg_polygon);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
class Line_ND : public Geometry_ND
{
public:
// Constructor, initializes the array
Line_ND(const unsigned &arg_dim = 2);
// Copy constructor
Line_ND(const Line_ND &arg_line);
// assignment operator
Line_ND &operator=(const Line_ND &arg_line);
// print the geometry
void print_geometry(ofstream &arg_ofs);
// parse the cin to the geometry
void parse_geometry(ifstream &arg_ifs);
};
const unsigned line_num_of_vertex = 2;
// Ref: https://stackoverflow.com/q/9621893
void print_output_file(int argc, char *argv[])
{
ifstream ans_ifs(argv[2], ios::in | ios::binary);
if (!ans_ifs)
{
cout << "Error: Cannot open output file" << endl;
exit(1);
}
char ans_block = 0;
unsigned offset_count = 0;
ans_ifs.read(&ans_block, 1);
while (!ans_ifs.eof())
{
int z = ans_block & 0xff;
cout << std::hex
<< std::setfill('0')
<< std::setw(2)
<< z
<< " ";
offset_count++;
if (offset_count % 16 == 0)
{
cout << endl;
}
ans_ifs.read(&ans_block, 1);
}
cout << endl;
ans_ifs.close();
}
// Point_ND class implementation
// Constructor
Point_ND::Point_ND(const unsigned &arg_dim)
: m_dim(arg_dim), m_coords(arg_dim)
{
}
// Copy constructor
Point_ND::Point_ND(const Point_ND &arg_point)
: m_dim(arg_point.m_dim), m_coords(arg_point.m_coords)
{
}
// assignment operator
Point_ND &Point_ND::operator=(const Point_ND &arg_point)
{
if (this != &arg_point)
{
m_dim = arg_point.m_dim;
m_coords = arg_point.m_coords;
}
return *this;
}
// get dimension
unsigned Point_ND::get_dim() const
{
return m_dim;
}
// get coordinates
vector<double> Point_ND::get_coords() const
{
return m_coords;
}
// set coordinates
void Point_ND::set_coords(const vector<double> &arg_coords)
{
m_coords = arg_coords;
}
// write data members in binary format
void Point_ND::write_binary_coords(ofstream &arg_ofs)
{
for (unsigned i = 0; i < m_dim; i++)
{
arg_ofs.write((char *)&m_coords[i], sizeof(double));
}
}
// read data members in binary format
void Point_ND::read_binary_coords(ifstream &arg_ifs)
{
double temp_double;
for (unsigned i = 0; i < m_dim; i++)
{
arg_ifs.read((char *)&temp_double, sizeof(double));
m_coords[i] = temp_double;
}
}
// Geometry_ND class implementation
// Constructor, initializes the array
Geometry_ND::Geometry_ND(const unsigned &arg_dim, const unsigned int &arg_num_of_vertex)
: m_dim(arg_dim), m_point_array(arg_num_of_vertex)
{
}
// Copy constructor
Geometry_ND::Geometry_ND(const Geometry_ND &arg_geometry)
: m_dim(arg_geometry.m_dim), m_point_array(arg_geometry.m_point_array)
{
}
// assignment operator
Geometry_ND &Geometry_ND::operator=(const Geometry_ND &arg_geometry)
{
if (this == &arg_geometry) // self-assignment
return *this;
m_point_array = arg_geometry.m_point_array;
return *this;
}
// print the geometry
void Geometry_ND::print_geometry(ofstream &arg_ofs)
{
throw runtime_error("print_geometry() is not implemented");
}
// parse the cin to the geometry
void Geometry_ND::parse_geometry(ifstream &arg_ifs)
{
throw runtime_error("parse_geometry() is not implemented");
}
// set the geometry
void Geometry_ND::set_geometry(const vector<Point_ND> &arg_point_array)
{
// check the dimension
for (unsigned i = 0; i < arg_point_array.size(); i++)
{
if (arg_point_array[i].get_dim() != m_dim)
{
throw runtime_error("The dimension of the geometry is not consistent");
}
}
m_point_array = arg_point_array;
}
// get the geometry array
vector<Point_ND> Geometry_ND::get_geometry_array()
{
return m_point_array;
}
// Triangle_ND class implementation
// Constructor, initializes the array
Triangle_ND::Triangle_ND(const unsigned &arg_dim)
: Geometry_ND(arg_dim, triangle_num_of_vertex)
{
}
// Copy constructor
Triangle_ND::Triangle_ND(const Triangle_ND &arg_triangle)
: Geometry_ND(arg_triangle)
{
}
// assignment operator
Triangle_ND &Triangle_ND::operator=(const Triangle_ND &arg_triangle)
{
if (this == &arg_triangle) // self-assignment
return *this;
Geometry_ND::operator=(arg_triangle);
return *this;
}
// print the geometry
void Triangle_ND::print_geometry(ofstream &arg_ofs)
{
unsigned num_of_vertex = m_point_array.size();
arg_ofs.write("t", 1);
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (int i = 0; i < num_of_vertex; i++)
{
m_point_array[i].write_binary_coords(arg_ofs);
}
}
// parse the cin to the geometry
void Triangle_ND::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num != triangle_num_of_vertex)
{
throw runtime_error("Triangle_ND::parse_geometry(): wrong vertex number");
}
for (int i = 0; i < vertex_num; i++)
{
Point_ND point(m_dim);
point.read_binary_coords(arg_ifs);
m_point_array[i] = point;
}
}
// Polygon_ND class implementation
// Constructor, initializes the array
Polygon_ND::Polygon_ND(const unsigned &arg_dim)
: Geometry_ND(arg_dim)
{
}
// Copy constructor
Polygon_ND::Polygon_ND(const Polygon_ND &arg_polygon)
: Geometry_ND(arg_polygon)
{
}
// assignment operator
Polygon_ND &Polygon_ND::operator=(const Polygon_ND &arg_polygon)
{
if (this == &arg_polygon) // self-assignment
return *this;
Geometry_ND::operator=(arg_polygon);
return *this;
}
// print the geometry
void Polygon_ND::print_geometry(ofstream &arg_ofs)
{
unsigned num_of_vertex = m_point_array.size();
arg_ofs.write("p", 1);
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (int i = 0; i < num_of_vertex; i++)
{
m_point_array[i].write_binary_coords(arg_ofs);
}
}
// parse the cin to the geometry
void Polygon_ND::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num < 3)
{
throw runtime_error("Polygon_ND::parse_geometry(): wrong vertex number");
}
m_point_array.resize(vertex_num);
for (int i = 0; i < vertex_num; i++)
{
Point_ND point(m_dim);
point.read_binary_coords(arg_ifs);
m_point_array[i] = point;
}
}
// Line_ND class implementation
// Constructor, initializes the array
Line_ND::Line_ND(const unsigned &arg_dim)
: Geometry_ND(arg_dim, line_num_of_vertex)
{
}
// Copy constructor
Line_ND::Line_ND(const Line_ND &arg_line)
: Geometry_ND(arg_line)
{
}
// assignment operator
Line_ND &Line_ND::operator=(const Line_ND &arg_line)
{
if (this == &arg_line) // self-assignment
return *this;
Geometry_ND::operator=(arg_line);
return *this;
}
// print the geometry
void Line_ND::print_geometry(ofstream &arg_ofs)
{
unsigned num_of_vertex = m_point_array.size();
arg_ofs.write("l", 1);
arg_ofs.write((char *)&num_of_vertex, sizeof(unsigned int));
for (int i = 0; i < num_of_vertex; i++)
{
m_point_array[i].write_binary_coords(arg_ofs);
}
}
// parse the cin to the geometry
void Line_ND::parse_geometry(ifstream &arg_ifs)
{
unsigned int vertex_num;
arg_ifs.read((char *)&vertex_num, sizeof(unsigned int));
if (vertex_num != line_num_of_vertex)
{
throw runtime_error("Line_ND::parse_geometry(): wrong vertex number");
}
for (int i = 0; i < vertex_num; i++)
{
Point_ND point(m_dim);
point.read_binary_coords(arg_ifs);
m_point_array[i] = point;
}
}
int main(int argc, char *argv[])
{
vector<Geometry_ND *> geo_ptr_array;
string input_file_path(argv[1]);
string output_file_path(argv[2]);
// run codes with exception handling
try
{
char input;
unsigned dim;
Geometry_ND *geo_ptr;
// open the input file
ifstream infile(input_file_path, ios::in | ios::binary);
infile.exceptions(ios::badbit);
// open the output file
ofstream outfile(output_file_path, ios::out | ios::trunc | ios::binary);
outfile.exceptions(ios::badbit);
// read dimension
infile.read((char *)&dim, sizeof(unsigned));
if (dim < 2 || dim > 10)
{
throw runtime_error("main(): wrong dimension");
}
// read geometry
while (infile.get(input))
{
// check the geometry type
switch (input)
{
case 't':
geo_ptr = new Triangle_ND(dim);
break;
case 'p':
geo_ptr = new Polygon_ND(dim);
break;
case 'l':
geo_ptr = new Line_ND(dim);
break;
default:
throw runtime_error("main(): wrong geometry type");
}
if (input == 't' || input == 'p' || input == 'l')
{
// change exception mask
infile.exceptions(ios::badbit | ios::failbit | ios::eofbit);
// parse the infile to the geometry
geo_ptr->parse_geometry(infile);
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
// rollback the exception mask
infile.exceptions(ios::badbit);
}
else
{
throw runtime_error("main(): wrong geometry type");
}
}
// print the geometry
// first, print the dimension
outfile.write((char *)&dim, sizeof(unsigned));
// second, print the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->print_geometry(outfile);
}
// close the input & output file
infile.close();
outfile.close();
}
// catch the exception
catch (exception &e)
{
cout << "Error: Invalid input" << endl;
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
return 1;
}
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
print_output_file(argc, argv);
return 0;
}
Convert Text Version Input to Binary Version Input
/*** convert text version input to binary version input ***/
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>
using namespace std;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
int main(int argc, char *argv[])
{
if (argc != 3)
{
cout << "Usage: txt_to_bin <input_file> <output_file>" << endl;
return 1;
}
ifstream input_file(argv[1]);
ofstream output_file(argv[2], ios::binary | ios::trunc);
if (!input_file.is_open())
{
cout << "Could not open input file" << endl;
return 1;
}
if (!output_file.is_open())
{
cout << "Could not open output file" << endl;
return 1;
}
string line, temp;
unsigned num_of_vertices = 1;
// read dimensions
getline(input_file, line);
unsigned num_of_dimensions = stoul(line);
// write dimensions
output_file.write((char *)&num_of_dimensions, sizeof(unsigned));
while (getline(input_file, line))
{
// check the geometry type
switch (line[0])
{
case 't':
case 'p':
case 'l':
// get the number of vertices from the next line
getline(input_file, temp);
num_of_vertices = stoul(temp);
break;
default:
error_and_exit();
}
// write the geometry type
char geometry_type = line[0];
output_file.write(&geometry_type, 1);
// write the number of vertices
if (line[0] == 't' || line[0] == 'p' || line[0] == 'l')
{
output_file.write((char *)&num_of_vertices, sizeof(unsigned));
}
// convert the lines to binary
for (int i = 0; i < num_of_vertices; i++)
{
getline(input_file, line);
stringstream ss(line);
for (int j = 0; j < num_of_dimensions; j++)
{
getline(ss, temp, ',');
double value = stod(temp);
output_file.write((char *)&value, sizeof(double));
}
}
}
input_file.close();
output_file.close();
return 0;
}
Convert Binary Version Input/Output to Human-readable Input/Output & Dump HEX File
/*** convert binary version input to human-readable input & dump hex file ***/
#include <iostream>
#include <fstream>
#include <string>
#include <sstream>
#include <iomanip>
using namespace std;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
int main(int argc, char *argv[])
{
if (argc != 3)
{
cout << "Usage: bin_to_txt <input_file> <output_file>" << endl;
return 1;
}
ifstream input_file(argv[1], ios::binary);
ofstream output_file(argv[2], ios::trunc);
if (!input_file.is_open())
{
cout << "Could not open input file" << endl;
return 1;
}
if (!output_file.is_open())
{
cout << "Could not open output file" << endl;
return 1;
}
char input;
unsigned num_of_vertices = 1;
// read dimensions
unsigned num_of_dimensions = 2;
input_file.read((char *)&num_of_dimensions, sizeof(unsigned));
// write dimensions
output_file << "# " << num_of_dimensions << endl;
while (input_file.get(input))
{
// check the geometry type
switch (input)
{
case 't':
case 'p':
case 'l':
// get the number of vertices from the next line
input_file.read((char *)&num_of_vertices, sizeof(unsigned));
break;
default:
error_and_exit();
}
// write the geometry type
char geometry_type = input;
output_file << "# " << geometry_type << endl;
// write the number of vertices
if (geometry_type == 't' || geometry_type == 'p' || geometry_type == 'l')
{
output_file << "# " << num_of_vertices << endl;
}
// convert the lines to human-readable format
for (int i = 0; i < num_of_vertices; i++)
{
output_file << "# " << setprecision(15) << fixed;
for (int j = 0; j < num_of_dimensions; j++)
{
double temp;
input_file.read((char *)&temp, sizeof(double));
if (j != 0)
{
output_file << ",";
}
output_file << temp;
}
output_file << endl;
}
}
input_file.close();
input_file.open(argv[1], ios::binary);
output_file << "# Hex dump" << endl;
char file_block = 0;
unsigned offset_count = 0;
input_file.read(&file_block, 1);
while (!input_file.eof())
{
int z = file_block & 0xff;
output_file << std::hex
<< std::setfill('0')
<< std::setw(2)
<< z
<< " ";
offset_count++;
if (offset_count % 16 == 0)
{
output_file << endl;
}
input_file.read(&file_block, 1);
}
output_file << endl;
output_file.close();
return 0;
}
(Extra) C++ Image Export & Matplot++
Slides version: lecture16_slides.html Website version: lecture16.html
- Tutorial: Matplot++
- Installation
- Hello world
- Plot Functions
- Annotations
- Appearance
- Export to image
- Example: Plot a Geometry on Complex Plane
- Pratices
Installation
Windows + MinGW: Update gcc
Note: 須先完成 設定 VSCode 環境 (Windows + MinGW) 再進行下一步
Terminal:
# remove old gcc 8.1.0
scoop uninstall mingw
# install new gcc 12.1.0
scoop install mingw-winlibs
Linux/macOS: Install CMake
Terminal:
Linux
sudo apt install cmake
macOS
brew install cmake
Install gnuplot
Terminal:
Windows
scoop install gnuplot
Linux
sudo apt install gnuplot
macOS
brew install gnuplot
Note: 安裝完成後須重新啟動 VSCode 及重新打開 Terminal 才能生效
Update VSCode C/C++ Extension
Install C/C++ Extension Pack
Correct:
Install Matplot++
Download project file & open in VSCode:
- github link stevenokm/matplotplusplus-master.zip
- 解壓縮全部,解壓縮後會有一個
matplotplusplus-master目錄 - 使用 VSCode 打開
matplotplusplus-master目錄
Build Matplot++ & Test Matplot++
- configure project "matplotplusplus-master" (Yes)
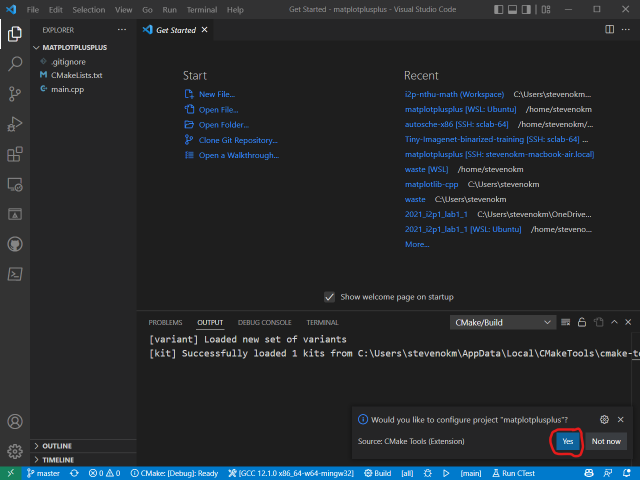
- select right active kit
- Windows:
GCC 12.1.0 x86_64-w64-mingw32 - Linux:
GCC 9.4.0 x86_64-linux-gnu(Ubuntu 20.04) - macOS:
Clang 13.0.0 arm64-apple-darwin20.6.0(macOS Big Sur, Apple Silicon)
- Windows:
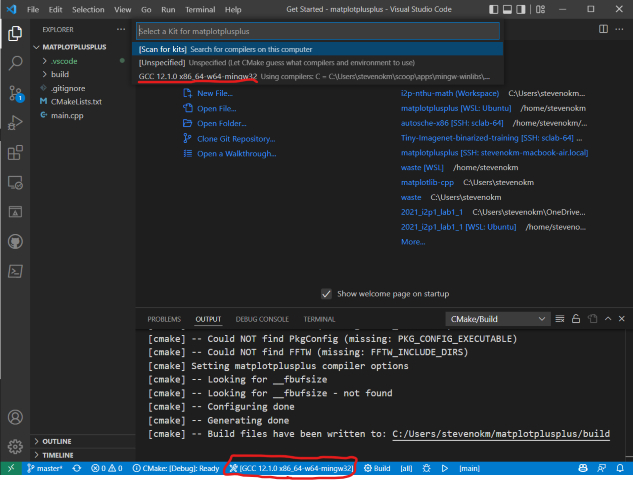
- Press "Build" button on the bottom of the VSCode window
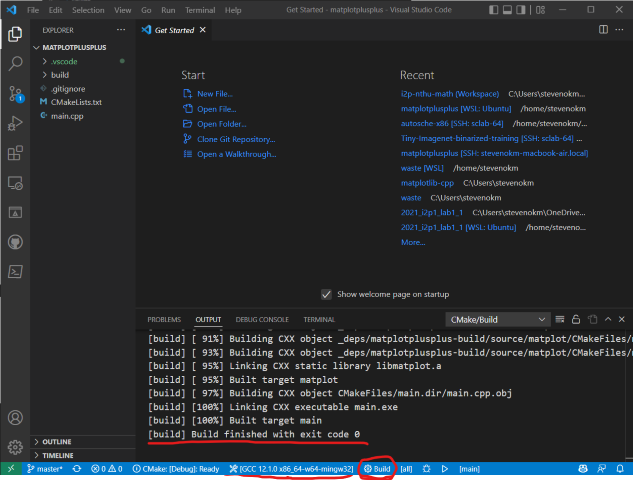
- Press "Run" button on the bottom of the VSCode window
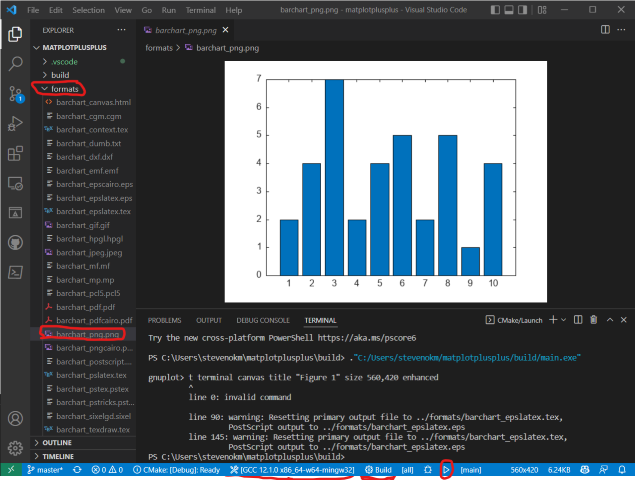
- Press "Debug" button on the bottom of the VSCode window to debug
Note 要注意 CMake 的設定是在 Debug CMake: [Debug] 下執行的
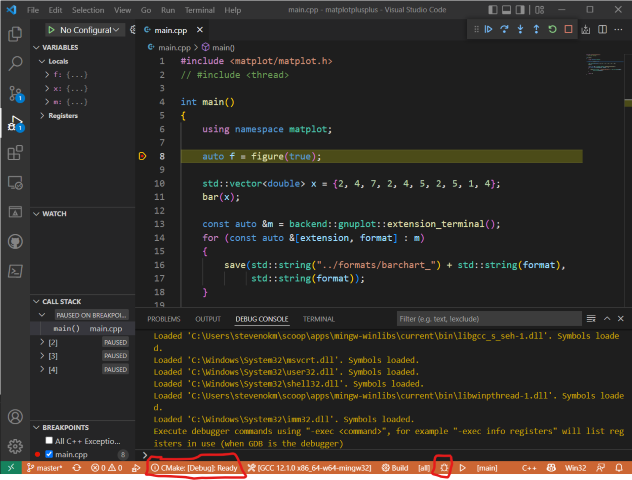
Hello world
Ref: Bar Plot - Matplot++
#include <cmath>
#include <matplot/matplot.h>
int main()
{
using namespace matplot;
std::vector<double> y = {75, 91, 105, 123.5, 131, 150,
179, 203, 226, 249, 281.5};
bar(y);
show();
return 0;
}
Result:
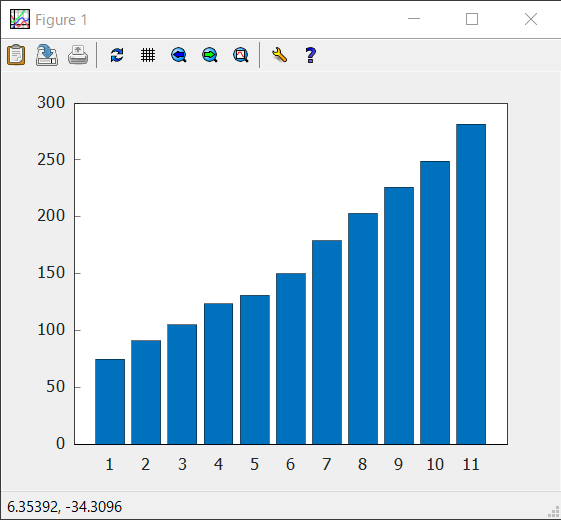
Plot Functions
- Line Plot
- Histogram
- Scatter Plot
- Bar Plot
- Pareto Chat
- Polar Line Plot
Line Plot
#include <cmath>
#include <matplot/matplot.h>
int main()
{
using namespace matplot;
std::vector<int> y = {2, 4, 7, 7, 6, 3, 9, 7, 3, 5};
plot(y);
show();
return 0;
}
Result:
Histogram
#include <cmath>
#include <matplot/matplot.h>
#include <random>
int main()
{
using namespace matplot;
std::vector<double> x = randn(10000, 0, 1);
auto h = hist(x);
std::cout << "Histogram with " << h->num_bins() << " bins" << std::endl;
show();
return 0;
}
Result:
Scatter Plot
#include <matplot/matplot.h>
#include <random>
int main()
{
using namespace matplot;
auto x = linspace(0, 3 * pi, 200);
auto y = transform(x, [&](double x)
{ return cos(x) + rand(0, 1); });
scatter(x, y);
show();
return 0;
}
Result:
Bar Plot
Ref: Bar Plot - Matplot++
#include <cmath>
#include <matplot/matplot.h>
#include <random>
int main()
{
using namespace matplot;
std::vector<std::vector<double>> Y = {
{2, 2, 2, 2}, {2, 5, 8, 11}, {3, 6, 9, 12}};
bar(Y);
show();
return 0;
}
Result:
Pareto Chat
#include <cmath>
#include <matplot/matplot.h>
#include <random>
int main()
{
using namespace matplot;
std::vector<double> codelines = {200, 120, 555, 608, 1024, 101, 57, 687};
std::vector<std::string> coders = {"Fred", "Ginger", "Norman", "Max",
"Julia", "Wally", "Heidi", "Pat"};
pareto(codelines, coders);
title("Lines of Code by Programmer");
show();
return 0;
}
Result:
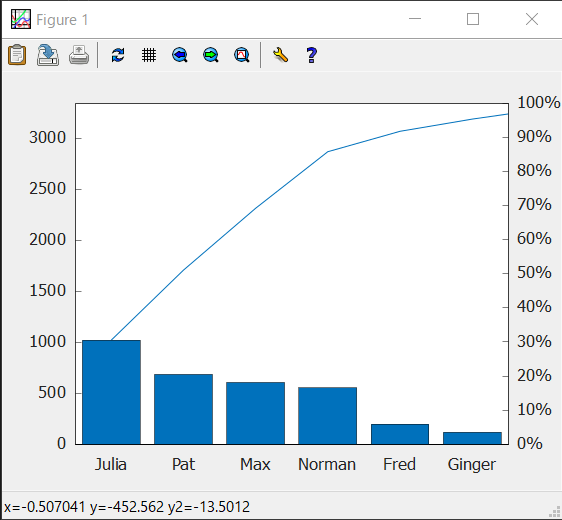
Polar Line Plot
Ref: Polar Line Plot - Matplot++
#include <cmath>
#include <matplot/matplot.h>
int main()
{
using namespace matplot;
std::vector<double> theta_degrees = linspace(0, 360, 50);
std::vector<double> rho =
transform(theta_degrees, [](auto t)
{ return 0.005 * t / 10.; });
std::vector<double> theta_radians = deg2rad(theta_degrees);
polarplot(theta_radians, rho);
show();
return 0;
}
Result:
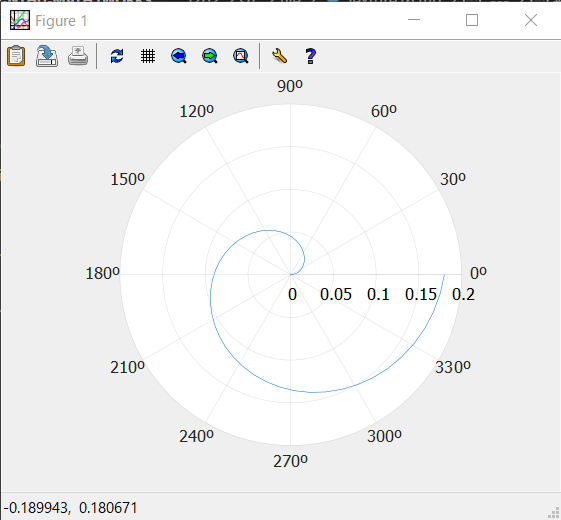
Annotations
- Text
- Text with Arrow
- Rectangle
- Textbox
Text
Ref: Text - Matplot++
#include <cmath>
#include <matplot/matplot.h>
int main()
{
using namespace matplot;
std::vector<double> x = linspace(-5, +5);
std::vector<double> y =
transform(x, [](auto x)
{ return pow(x, 3) - 12 * x; });
plot(x, y);
std::vector<double> xt = {-2, +2};
std::vector<double> yt = {16, -16};
std::string str = "dy/dx = 0";
text(xt, yt, str);
show();
return 0;
}
Result:
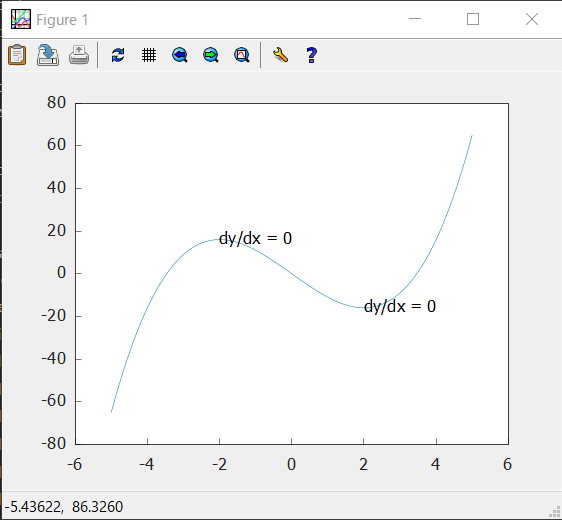
Text with Arrow
Ref: Text with Arrow - Matplot++
#include <cmath>
#include <matplot/matplot.h>
int main()
{
using namespace matplot;
plot(iota(1, 10));
auto [t, a] = textarrow(2.5, 6.5, 5, 5, "y=x");
t->color("red").font_size(14);
a->color("blue");
show();
return 0;
}
Result:
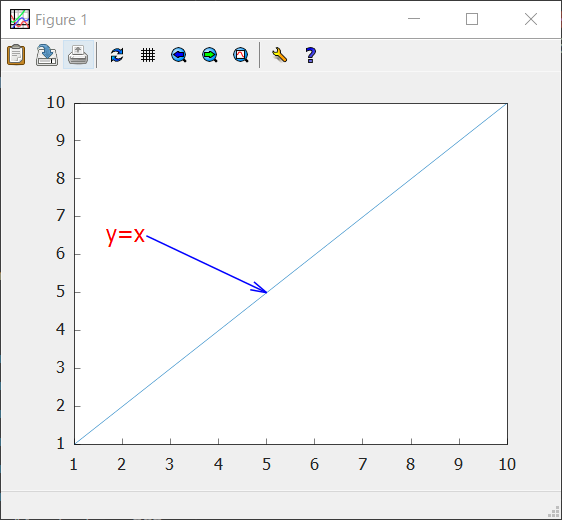
Rectangle
#include <cmath>
#include <matplot/matplot.h>
int main()
{
using namespace matplot;
rectangle(2, 4, 2, 2, 1.);
auto r2 = rectangle(2, 4, 2, 2, 0.);
r2->color("red");
axis(equal);
show();
return 0;
}
Result:
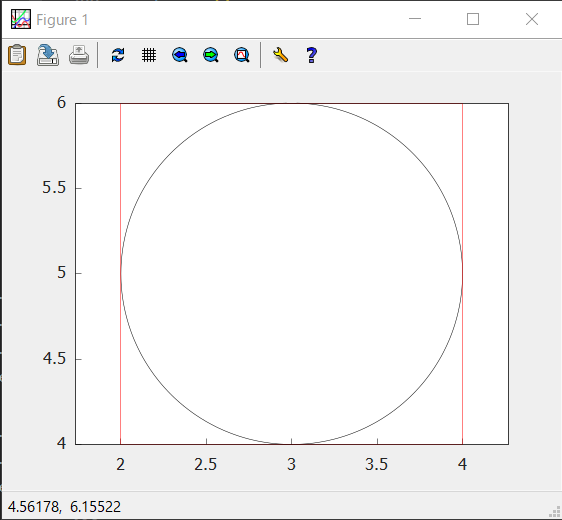
Textbox
Ref: Textbox - Matplot++
#include <cmath>
#include <matplot/matplot.h>
int main()
{
using namespace matplot;
plot(iota(1, 10));
textbox(2, 8, 4, 0.5, "String line from 1 to 10");
show();
return 0;
}
Result:
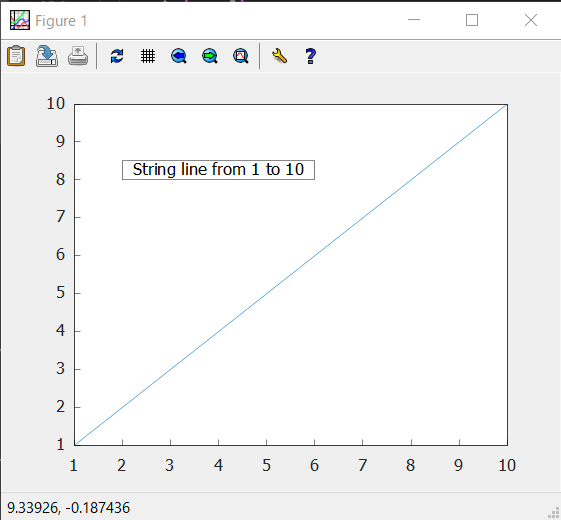
Export to image
- Manually
- Programmatically
Manually
- Click on the
Export to imagebutton
- Type filename
ProgProgrammatically
Export files with save()
#include <cmath>
#include <matplot/matplot.h>
int main()
{
using namespace matplot;
plot(iota(1, 10));
textbox(2, 8, 4, 0.5, "String line from 1 to 10");
// show();
// windows gnuplot bug workaround
save("../textbox_export.png");
// export to file with fileextension .png
save("../textbox_export.png");
// or with filename and filetype
save("../textbox_export", "svg");
return 0;
}
Result: textbox_export.png
Result: textbox_export.svg
Example: Plot a Geometry on Complex Plane [Source]
Pratices
- Draw & Save
Triangle_2Din 2D plane by matplot++ - Draw & Save
Triangle_Compin Polar Complex plane by matplot++
Example: Plot a Geometry on Complex Plane
#include <iostream>
#include <string>
#include <sstream>
#include <cmath>
#include <vector>
#include <limits>
#include <matplot/matplot.h>
using namespace std;
class Geometry_Comp;
class Complex
{
private:
// data members
// save the real and imaginary parts of the complex number
// with `double` precision
double m_real;
double m_imag;
public:
// Constructor, initializes real and imaginary parts
Complex(const double &arg_real = 0.0, const double &arg_imag = 0.0);
// Copy constructor
Complex(const Complex &arg_c);
// assignment operator
Complex &operator=(const Complex &arg_c);
// add assignment operator
Complex &operator+=(const Complex &arg_c);
// multiply assignment operator
Complex &operator*=(const Complex &arg_c);
// length of the complex number
double length() const;
// angle of the complex number in radians
double angle() const;
// get real
double get_real() const;
// get imaginary
double get_imag() const;
// cout `<<` operator for print complex number
// note: be careful about the format of output
friend ostream &operator<<(ostream &arg_os, const Complex &arg_c);
// cin `>>` operator for input complex number
// note: use `>>` to parse the string to double,
// use `istream::fail()` to check the conversion is successful
// and use `istream::eof()` to check the is parse to the end of line
friend istream &operator>>(istream &arg_is, Complex &arg_c);
// friend class
friend class Geometry_Comp;
};
class Geometry_Comp
{
protected:
// data members
vector<Complex> m_comp_array;
// utility function to check if the transformation is valid
bool _check_transform(const Complex &arg_trans_c, const char &arg_op);
public:
// Constructor, initializes the array
Geometry_Comp(const unsigned int &arg_num_of_vertex = 0);
// Copy constructor
Geometry_Comp(const Geometry_Comp &arg_gc);
// assignment operator
Geometry_Comp &operator=(const Geometry_Comp &arg_gc);
// print the geometry
virtual void print_geometry();
// parse the cin to the geometry
virtual void parse_geometry(istream &arg_is);
// export the geometry to a file
virtual void export_geometry(const string &arg_file_name,
const string &arg_file_type);
// apply transformation to the geometry
void transform_geometry(const Complex &arg_trans_c, const char &arg_op);
// set the geometry
void set_geometry(const vector<Complex> &arg_comp_array);
// get the geometry array
vector<Complex> get_geometry_array();
};
class Triangle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Triangle_Comp();
// Copy constructor
Triangle_Comp(const Triangle_Comp &arg_tc);
// assignment operator
Triangle_Comp &operator=(const Triangle_Comp &arg_tc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
// export the geometry to a file
void export_geometry(const string &arg_file_name, const string &arg_file_type);
};
const unsigned triangle_num_of_vertex = 3;
class Quadrilateral_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Quadrilateral_Comp();
// Copy constructor
Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc);
// assignment operator
Quadrilateral_Comp &operator=(const Quadrilateral_Comp &arg_qc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
// export the geometry to a file
void export_geometry(const string &arg_file_name, const string &arg_file_type);
};
const unsigned quadrilateral_num_of_vertex = 4;
class Polygon_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Polygon_Comp();
// Copy constructor
Polygon_Comp(const Polygon_Comp &arg_pc);
// assignment operator
Polygon_Comp &operator=(const Polygon_Comp &arg_pc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
// export the geometry to a file
void export_geometry(const string &arg_file_name, const string &arg_file_type);
};
class Circle_Comp : public Geometry_Comp
{
public:
// Constructor, initializes the array
Circle_Comp();
// Copy constructor
Circle_Comp(const Circle_Comp &arg_cc);
// assignment operator
Circle_Comp &operator=(const Circle_Comp &arg_cc);
// print the geometry
void print_geometry();
// parse the cin to the geometry
void parse_geometry(istream &arg_is);
// export the geometry to a file
void export_geometry(const string &arg_file_name, const string &arg_file_type);
};
const unsigned circle_num_of_vertex = 2;
// error and exit
void error_and_exit()
{
cout << "Error: Invalid input" << endl;
exit(1);
}
// Complex class implementation
// Constructor, initializes real and imaginary parts
// hint: as like as `modify` function in examples
// but use default constructor to implement
Complex::Complex(const double &arg_real, const double &arg_imag)
: m_real(arg_real), m_imag(arg_imag)
{
}
// Copy constructor
Complex::Complex(const Complex &arg_c)
: m_real(arg_c.m_real), m_imag(arg_c.m_imag)
{
}
// assignment operator
Complex &Complex::operator=(const Complex &arg_c)
{
if (this == &arg_c) // self-assignment
return *this;
m_real = arg_c.m_real;
m_imag = arg_c.m_imag;
return *this;
}
// add assignment operator
Complex &Complex::operator+=(const Complex &arg_c)
{
m_real += arg_c.m_real;
m_imag += arg_c.m_imag;
return *this;
}
// multiply assignment operator
Complex &Complex::operator*=(const Complex &arg_c)
{
double real = m_real * arg_c.m_real - m_imag * arg_c.m_imag;
double imag = m_real * arg_c.m_imag + m_imag * arg_c.m_real;
m_real = real;
m_imag = imag;
return *this;
}
// length of the complex number
double Complex::length() const
{
return sqrt(m_real * m_real + m_imag * m_imag);
}
// angle of the complex number in radians
double Complex::angle() const
{
if (m_real == 0 && m_imag == 0)
{
return NAN;
}
return atan2(m_imag, m_real);
}
// get real
double Complex::get_real() const
{
return m_real;
}
// get imaginary
double Complex::get_imag() const
{
return m_imag;
}
// cout `<<` operator for print complex number
// note: be careful about the format of output
ostream &operator<<(ostream &arg_os, const Complex &arg_c)
{
if (arg_c.m_imag > 0)
{
arg_os << arg_c.m_real << " + " << arg_c.m_imag << "i";
}
else if (arg_c.m_imag < 0)
{
arg_os << arg_c.m_real << " - " << -arg_c.m_imag << "i";
}
else
{
arg_os << arg_c.m_real;
}
return arg_os;
}
// cin `>>` operator for input complex number
// note: be careful about the format of input
istream &operator>>(istream &arg_is, Complex &arg_c)
{
double input_real, input_imag;
arg_is >> input_real;
if (arg_is.fail())
{
error_and_exit();
}
arg_is >> input_imag;
if (arg_is.fail() || !arg_is.eof())
{
error_and_exit();
}
arg_c.m_real = input_real;
arg_c.m_imag = input_imag;
return arg_is;
}
// Geometry_Comp class implementation
// check if the transformation is valid
bool Geometry_Comp::_check_transform(const Complex &arg_c, const char &arg_op)
{
// check if the operation is valid
if (arg_op == 'r' && (arg_c.length() != 1 || isnan(arg_c.angle())))
{
return false;
}
else if (arg_op == 'z' && (arg_c.m_real == 0 || arg_c.m_imag != 0))
{
return false;
}
else
{
return true;
}
}
// Constructor, initializes the array
Geometry_Comp::Geometry_Comp(const unsigned int &arg_num_of_vertex)
: m_comp_array(arg_num_of_vertex)
{
}
// Copy constructor
Geometry_Comp::Geometry_Comp(const Geometry_Comp &arg_gc)
: m_comp_array(arg_gc.m_comp_array)
{
}
// assignment operator
Geometry_Comp &Geometry_Comp::operator=(const Geometry_Comp &arg_gc)
{
if (this == &arg_gc) // self-assignment
return *this;
m_comp_array = arg_gc.m_comp_array;
return *this;
}
// print the geometry
void Geometry_Comp::print_geometry()
{
cout << "not implemented" << endl;
}
// parse the cin to the geometry
void Geometry_Comp::parse_geometry(istream &arg_is)
{
cout << "not implemented" << endl;
}
// export the geometry to a file
void Geometry_Comp::export_geometry(const string &arg_file_name,
const string &arg_file_type)
{
cout << "not implemented" << endl;
}
// apply transformation to the geometry
void Geometry_Comp::transform_geometry(const Complex &arg_c, const char &arg_op)
{
if (!(_check_transform(arg_c, arg_op)))
{
error_and_exit();
}
if (arg_op == 'm')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] += arg_c;
}
}
else if (arg_op == 'r' || arg_op == 'z')
{
for (unsigned int i = 0; i < m_comp_array.size(); i++)
{
m_comp_array[i] *= arg_c;
}
}
}
// set the geometry
void Geometry_Comp::set_geometry(const vector<Complex> &arg_comp_array)
{
m_comp_array = arg_comp_array;
}
// get the geometry array
vector<Complex> Geometry_Comp::get_geometry_array()
{
return m_comp_array;
}
// Triangle_Comp class implementation
// Constructor, initializes the array
Triangle_Comp::Triangle_Comp()
: Geometry_Comp(triangle_num_of_vertex)
{
}
// Copy constructor
Triangle_Comp::Triangle_Comp(const Triangle_Comp &arg_tc)
: Geometry_Comp(arg_tc)
{
}
// assignment operator
Triangle_Comp &Triangle_Comp::operator=(const Triangle_Comp &arg_tc)
{
if (this == &arg_tc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_tc);
return *this;
}
// print the geometry
void Triangle_Comp::print_geometry()
{
cout << "t" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < triangle_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Triangle_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
stringstream ss(temp);
unsigned int vertex_num;
ss >> vertex_num;
if (vertex_num != triangle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// export the geometry to a file
void Triangle_Comp::export_geometry(const string &arg_file_name,
const string &arg_file_type)
{
double x_min = numeric_limits<double>::max();
double y_min = numeric_limits<double>::max();
double x_max = numeric_limits<double>::min();
double y_max = numeric_limits<double>::min();
for (int i = 0; i < triangle_num_of_vertex; i++)
{
double current_x1 = m_comp_array[i].get_real();
double current_y1 = m_comp_array[i].get_imag();
double current_x2 = m_comp_array[(i + 1) % triangle_num_of_vertex].get_real();
double current_y2 = m_comp_array[(i + 1) % triangle_num_of_vertex].get_imag();
matplot::line(current_x1, current_y1, current_x2, current_y2);
// update the bounding box
x_min = min(x_min, current_x1);
y_min = min(y_min, current_y1);
x_max = max(x_max, current_x1);
y_max = max(y_max, current_y1);
x_min = min(x_min, current_x2);
y_min = min(y_min, current_y2);
x_max = max(x_max, current_x2);
y_max = max(y_max, current_y2);
}
matplot::title("Triangle");
matplot::xlabel("real");
matplot::ylabel("imag");
matplot::axis({x_min - 0.1 * (x_max - x_min),
x_max + 0.1 * (x_max - x_min),
y_min - 0.1 * (y_max - y_min),
y_max + 0.1 * (y_max - y_min)});
// windows bug workaround
matplot::save(arg_file_name, arg_file_type);
// save the figure
matplot::save(arg_file_name, arg_file_type);
// clear the figure
matplot::cla();
}
// Quadrilateral_Comp class implementation
// Constructor, initializes the array
Quadrilateral_Comp::Quadrilateral_Comp()
: Geometry_Comp(quadrilateral_num_of_vertex)
{
}
// Copy constructor
Quadrilateral_Comp::Quadrilateral_Comp(const Quadrilateral_Comp &arg_qc)
: Geometry_Comp(arg_qc)
{
}
// assignment operator
Quadrilateral_Comp &Quadrilateral_Comp::operator=(const Quadrilateral_Comp &arg_qc)
{
if (this == &arg_qc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_qc);
return *this;
}
// print the geometry
void Quadrilateral_Comp::print_geometry()
{
cout << "q" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < quadrilateral_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Quadrilateral_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != quadrilateral_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// export the geometry to a file
void Quadrilateral_Comp::export_geometry(const string &arg_file_name,
const string &arg_file_type)
{
double x_min = numeric_limits<double>::max();
double y_min = numeric_limits<double>::max();
double x_max = numeric_limits<double>::min();
double y_max = numeric_limits<double>::min();
for (int i = 0; i < quadrilateral_num_of_vertex; i++)
{
double current_x1 = m_comp_array[i].get_real();
double current_y1 = m_comp_array[i].get_imag();
double current_x2 = m_comp_array[
(i + 1) % quadrilateral_num_of_vertex].get_real();
double current_y2 = m_comp_array[
(i + 1) % quadrilateral_num_of_vertex].get_imag();
matplot::line(current_x1, current_y1, current_x2, current_y2);
// update the bounding box
x_min = min(x_min, current_x1);
y_min = min(y_min, current_y1);
x_max = max(x_max, current_x1);
y_max = max(y_max, current_y1);
x_min = min(x_min, current_x2);
y_min = min(y_min, current_y2);
x_max = max(x_max, current_x2);
y_max = max(y_max, current_y2);
}
matplot::title("Quadrilateral");
matplot::xlabel("real");
matplot::ylabel("imag");
matplot::axis({x_min - 0.1 * (x_max - x_min),
x_max + 0.1 * (x_max - x_min),
y_min - 0.1 * (y_max - y_min),
y_max + 0.1 * (y_max - y_min)});
// windows bug workaround
matplot::save(arg_file_name, arg_file_type);
// save the figure
matplot::save(arg_file_name, arg_file_type);
// clear the figure
matplot::cla();
}
// Polygon_Comp class implementation
// Constructor, initializes the array
Polygon_Comp::Polygon_Comp()
: Geometry_Comp()
{
}
// Copy constructor
Polygon_Comp::Polygon_Comp(const Polygon_Comp &arg_pc)
: Geometry_Comp(arg_pc)
{
}
// assignment operator
Polygon_Comp &Polygon_Comp::operator=(const Polygon_Comp &arg_pc)
{
if (this == &arg_pc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_pc);
return *this;
}
// print the geometry
void Polygon_Comp::print_geometry()
{
cout << "p" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < m_comp_array.size(); i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Polygon_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num < triangle_num_of_vertex)
{
error_and_exit();
}
m_comp_array.resize(vertex_num);
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// export the geometry to a file
void Polygon_Comp::export_geometry(const string &arg_file_name,
const string &arg_file_type)
{
double x_min = numeric_limits<double>::max();
double y_min = numeric_limits<double>::max();
double x_max = numeric_limits<double>::min();
double y_max = numeric_limits<double>::min();
for (int i = 0; i < m_comp_array.size(); i++)
{
double current_x1 = m_comp_array[i].get_real();
double current_y1 = m_comp_array[i].get_imag();
double current_x2 = m_comp_array[(i + 1) % m_comp_array.size()].get_real();
double current_y2 = m_comp_array[(i + 1) % m_comp_array.size()].get_imag();
matplot::line(current_x1, current_y1, current_x2, current_y2);
// update the bounding box
x_min = min(x_min, current_x1);
y_min = min(y_min, current_y1);
x_max = max(x_max, current_x1);
y_max = max(y_max, current_y1);
x_min = min(x_min, current_x2);
y_min = min(y_min, current_y2);
x_max = max(x_max, current_x2);
y_max = max(y_max, current_y2);
}
matplot::title("Polygon");
matplot::xlabel("real");
matplot::ylabel("imag");
matplot::axis({x_min - 0.1 * (x_max - x_min),
x_max + 0.1 * (x_max - x_min),
y_min - 0.1 * (y_max - y_min),
y_max + 0.1 * (y_max - y_min)});
// windows bug workaround
matplot::save(arg_file_name, arg_file_type);
// save the figure
matplot::save(arg_file_name, arg_file_type);
// clear the figure
matplot::cla();
}
// Circle_Comp class implementation
// Constructor, initializes the array
Circle_Comp::Circle_Comp()
: Geometry_Comp(circle_num_of_vertex)
{
}
// Copy constructor
Circle_Comp::Circle_Comp(const Circle_Comp &arg_cc)
: Geometry_Comp(arg_cc)
{
}
// assignment operator
Circle_Comp &Circle_Comp::operator=(const Circle_Comp &arg_cc)
{
if (this == &arg_cc) // self-assignment
return *this;
Geometry_Comp::operator=(arg_cc);
return *this;
}
// print the geometry
void Circle_Comp::print_geometry()
{
cout << "c" << endl;
cout << m_comp_array.size() << endl;
for (int i = 0; i < circle_num_of_vertex; i++)
{
cout << m_comp_array[i] << endl;
}
}
// parse the cin to the geometry
void Circle_Comp::parse_geometry(istream &arg_is)
{
string temp;
getline(arg_is, temp); // get the vertex number
int vertex_num = stoi(temp);
if (vertex_num != circle_num_of_vertex)
{
error_and_exit();
}
for (int i = 0; i < vertex_num; i++)
{
getline(arg_is, temp);
stringstream ss(temp);
Complex c;
ss >> c;
if (ss.fail())
{
error_and_exit();
}
m_comp_array[i] = c;
}
}
// export the geometry to a file
void Circle_Comp::export_geometry(const string &arg_file_name,
const string &arg_file_type)
{
double x_min = min(m_comp_array[0].get_real(), m_comp_array[1].get_real());
double y_min = min(m_comp_array[0].get_imag(), m_comp_array[1].get_imag());
double x_delta = abs(m_comp_array[1].get_real() - m_comp_array[0].get_real());
double y_delta = abs(m_comp_array[1].get_imag() - m_comp_array[0].get_imag());
double radius = min(x_delta, y_delta) / 2;
matplot::rectangle(x_min, y_min, x_delta, y_delta, radius);
matplot::title("Circle");
matplot::xlabel("real");
matplot::ylabel("imag");
matplot::axis({x_min - 0.1 * x_delta,
x_min + 1.1 * x_delta,
y_min - 0.1 * y_delta,
y_min + 1.1 * y_delta});
// windows bug workaround
matplot::save(arg_file_name, arg_file_type);
// save the figure
matplot::save(arg_file_name, arg_file_type);
// clear the figure
matplot::cla();
}
int main()
{
string input, temp;
vector<Geometry_Comp *> geo_ptr_array;
Geometry_Comp *geo_ptr;
Complex trans_c;
char trans_op;
while (getline(cin, input))
{
// check the geometry type
switch (input[0])
{
case 't':
geo_ptr = new Triangle_Comp();
break;
case 'q':
geo_ptr = new Quadrilateral_Comp();
break;
case 'p':
geo_ptr = new Polygon_Comp();
break;
case 'c':
geo_ptr = new Circle_Comp();
break;
case 'r':
case 'z':
case 'm':
getline(cin, temp);
break;
default:
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
if (input[0] == 't' || input[0] == 'q' || input[0] == 'p' || input[0] == 'c')
{
// parse the cin to the geometry
geo_ptr->parse_geometry(cin);
// print the geometry
geo_ptr->print_geometry();
// push the pointer to the array
geo_ptr_array.push_back(geo_ptr);
}
else if (input[0] == 'r' || input[0] == 'z' || input[0] == 'm')
{
stringstream ss(temp);
ss >> trans_c;
// transform the geometry using operator and complex
for (int i = 0; i < geo_ptr_array.size(); i++)
{
geo_ptr_array[i]->transform_geometry(trans_c, input[0]);
// print transformed geometry
geo_ptr_array[i]->print_geometry();
}
}
else
{
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
error_and_exit();
}
}
// export each geometry to the file
for (int i = 0; i < geo_ptr_array.size(); i++)
{
string filename = "../geometry_" + to_string(i);
string filetype = "png";
geo_ptr_array[i]->export_geometry(filename, filetype);
}
// delete the geometry
for (int i = 0; i < geo_ptr_array.size(); i++)
{
delete geo_ptr_array[i];
}
return 0;
}
Input:
$ ./main
t⏎
3⏎
1.0 2.0⏎
3.0 4.0⏎
5.0 0.0⏎
t
3
1 + 2i
3 + 4i
5
q⏎
4⏎
1.0 2.0⏎
3.0 2.0⏎
3.0 4.0⏎
1.0 4.0⏎
q
4
1 + 2i
3 + 2i
3 + 4i
1 + 4i
c⏎
2⏎
1.0 2.0⏎
3.0 4.0⏎
c
2
1 + 2i
3 + 4i
p⏎
5⏎
1.0 0.0⏎
2.0 1.1⏎
-3.0 -2.2⏎
4.3 2.1⏎
-1.2 3.4⏎
p
5
1
2 + 1.1i
-3 - 2.2i
4.3 + 2.1i
-1.2 + 3.4i
^Z⏎
Result:
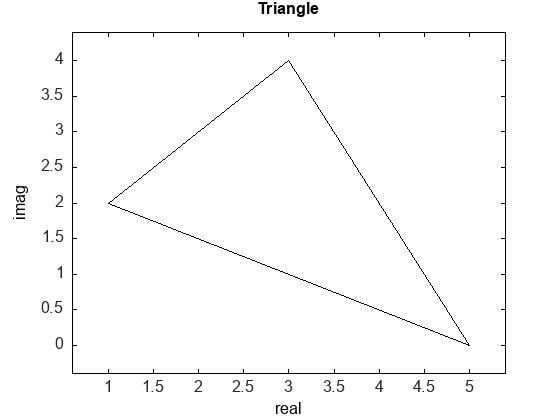
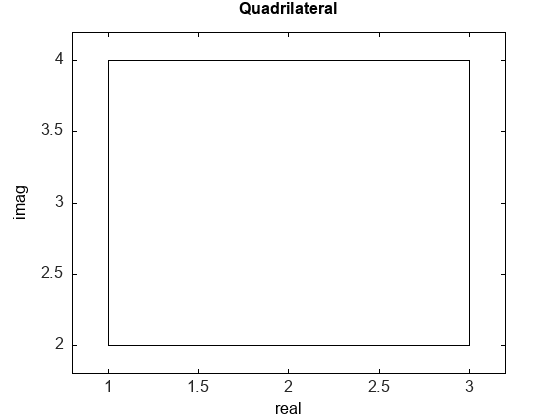
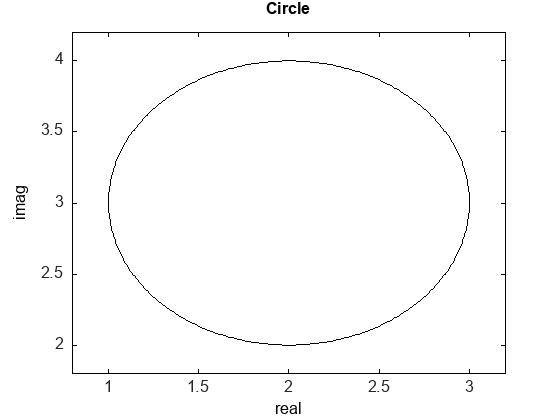
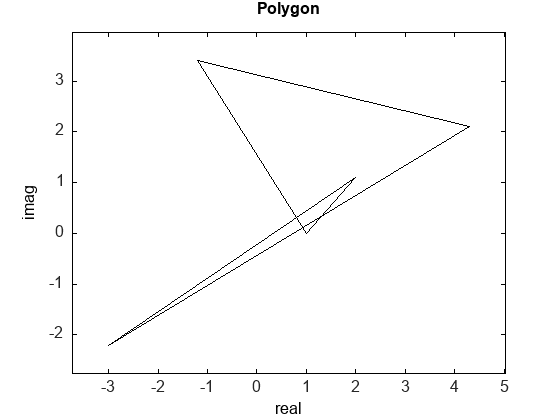
(Extra) Google Test for Class
Slides version: lecture18_slides.html Website version: lecture18.html
Prerequisite Lecture: Lecture 16: GoogleTest Tutorial
- Google Test
- Installation
- Hello world
- Google Test for Class
- What is Unit Test?
- Example: unit test for class (sample4 & sample5)
- Example: Unit Test for Vector & Matrix in Binary File (class ver.)
- Pratices
Installation
Windows + MinGW: Update gcc
Note: 須先完成 設定 VSCode 環境 (Windows + MinGW) 再進行下一步
Terminal:
# remove old gcc 8.1.0
scoop uninstall mingw
# install new gcc 12.1.0
scoop install mingw-winlibs
Linux/macOS: Install CMake
Terminal:
Linux
sudo apt install cmake
macOS
brew install cmake
Update VSCode C/C++ Extension
Install C/C++ Extension Pack
Correct:
Hello GoogleTest
Ref: Quickstart: Building with CMake
- 建立專案資料夾 (e.g.
googletest) - 使用 VSCode 打開專案資料夾
- 新增
hello_test.cpp&CMakeLists.txt,內容如下:
hello_test.cpp
#include <gtest/gtest.h>
// Demonstrate some basic assertions.
TEST(HelloTest, BasicAssertions)
{
// Expect two strings not to be equal.
EXPECT_STRNE("hello", "world");
// Expect equality.
EXPECT_EQ(7 * 6, 42);
}
CMakeLists.txt
cmake_minimum_required(VERSION 3.14)
project(hello_test)
# GoogleTest requires at least C++11
set(CMAKE_CXX_STANDARD 11)
include(FetchContent)
FetchContent_Declare(
googletest
URL https://github.com/google/googletest/archive/609281088cfefc76f9d0ce82e1ff6c30cc3591e5.zip
)
# For Windows: Prevent overriding the parent project's compiler/linker settings
set(gtest_force_shared_crt ON CACHE BOOL "" FORCE)
FetchContent_MakeAvailable(googletest)
enable_testing()
add_executable(
hello_test
hello_test.cpp
)
target_link_libraries(
hello_test
gtest_main
)
include(GoogleTest)
gtest_discover_tests(hello_test)
- 重新使用 VSCode 打開專案資料夾
- configure project "matplotplusplus-master" (Yes)
- select right active kit
- Windows:
GCC 12.1.0 x86_64-w64-mingw32 - Linux:
GCC 9.4.0 x86_64-linux-gnu(Ubuntu 20.04) - macOS:
Clang 13.0.0 arm64-apple-darwin20.6.0(macOS Big Sur, Apple Silicon)
- Windows:
- Press "Build" button on the bottom of the VSCode window
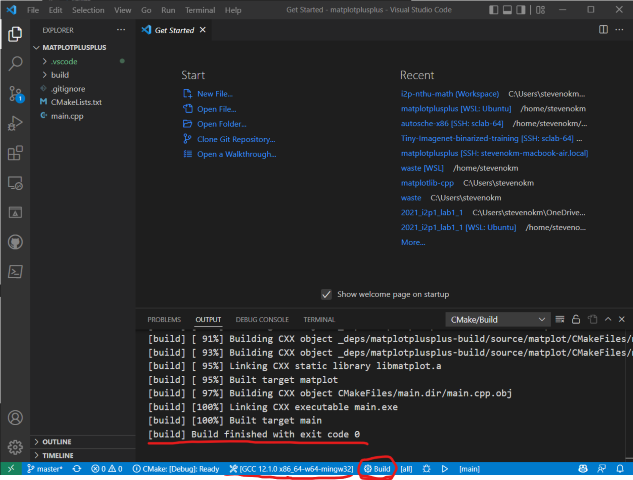
- Press "Run" button on the bottom of the VSCode window
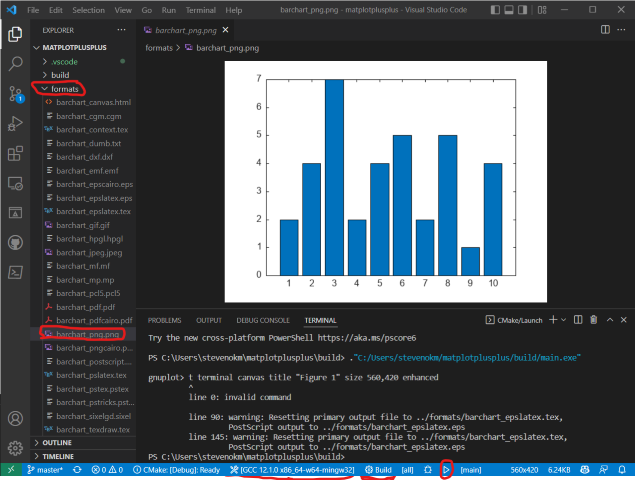
Terminal:
Running main() from C:\Users\stevenokm\googletest\build\_deps\googletest-src\googletest\src\gtest_main.cc
[==========] Running 1 test from 1 test suite.
[----------] Global test environment set-up.
[----------] 1 test from HelloTest
[ RUN ] HelloTest.BasicAssertions
[ OK ] HelloTest.BasicAssertions (0 ms)
[----------] 1 test from HelloTest (2 ms total)
[----------] Global test environment tear-down
[==========] 1 test from 1 test suite ran. (9 ms total)
[ PASSED ] 1 test.
Google Test for Class
Ref: Unit Testing | Software Testing
- What is Unit Test?
- Objective of Unit Testing
- Types of Unit Testing
- Unit Testing Techniques
- Example: unit test for class
What is Unit Test?
Unit Testing is a software testing technique by means of which individual units of software i.e. group of computer program modules, usage procedures, and operating procedures are tested to determine whether they are suitable for use or not.
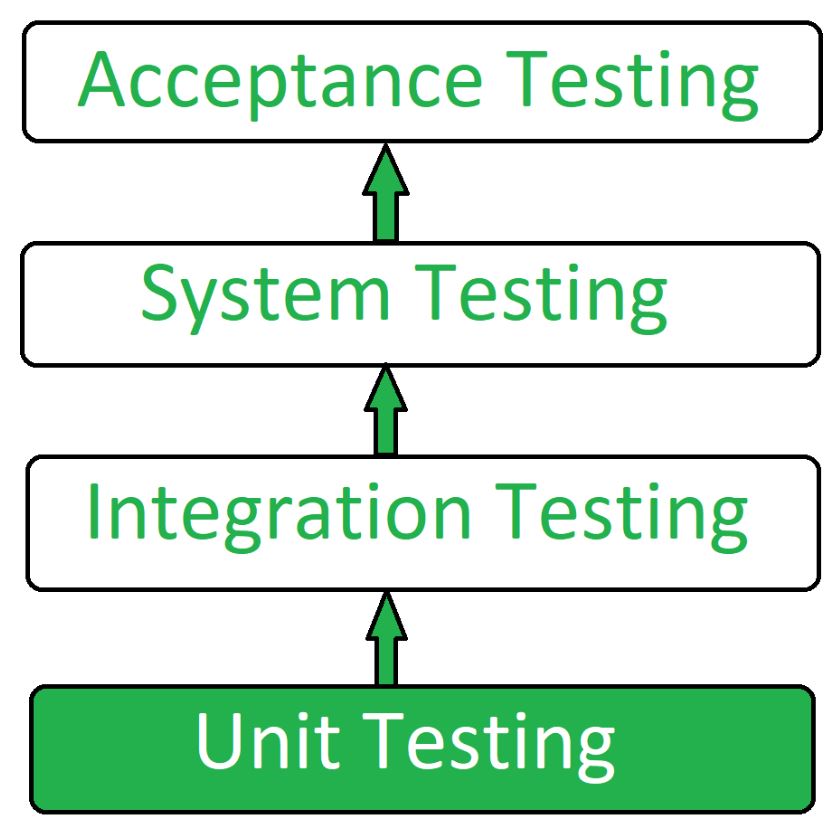
Objective of Unit Testing
- To isolate a section of code.
- To verify the correctness of the code.
- To test every function and procedure.
- To fix bugs early in the development cycle and to save costs.
- To help the developers to understand the code base and enable them to make changes quickly.
- To help with code reuse.
Types of Unit Testing
There are 3 types of Unit Testing Techniques. They are:
- Black Box Testing: This testing technique is used in covering the unit tests for input, user interface, and output parts.
- White Box Testing: This technique is used in testing the functional behavior of the system by giving the input and checking the functionality output including the internal design structure and code of the modules.
- Gray Box Testing: This technique is used in executing the relevant test cases, test methods, test functions, and analyzing the code performance for the modules.
Black Box Testing
Ref: Black-box testing - Wikipedia
Black-box testing is a method of software testing that examines the functionality of an application without peering into its internal structures or workings. This method of test can be applied virtually to every level of software testing: unit, integration, system and acceptance. It is sometimes referred to as specification-based testing.
System diagram:

White Box Testing
Ref: White-box testing - Wikipedia, File:WhiteBoxTesting.png
White-box testing is a method of software testing that tests internal structures or workings of an application, as opposed to its functionality (i.e. black-box testing). In white-box testing an internal perspective of the system, as well as programming skills, are used to design test cases.
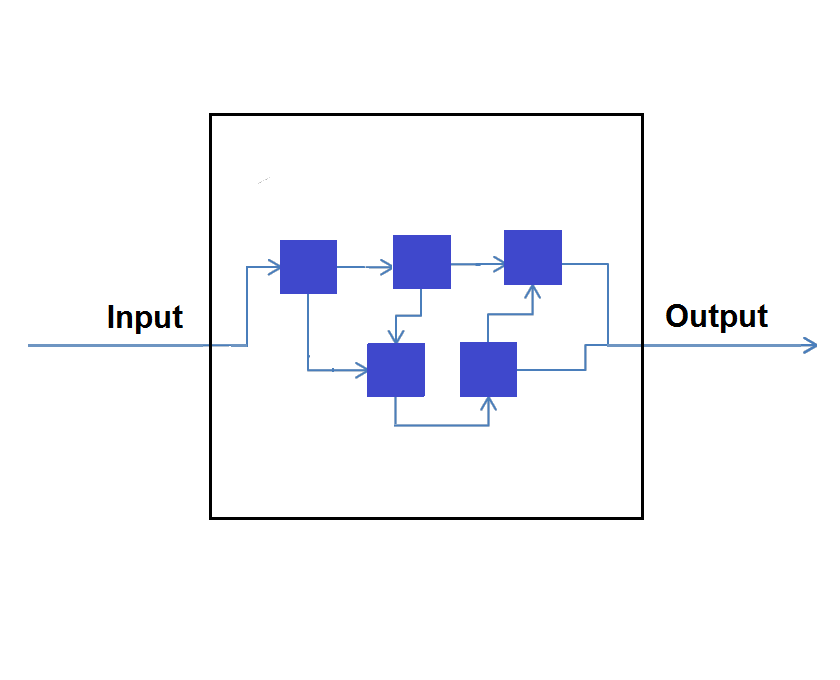
Gray Box Testing
Ref: Gray-box testing - Wikipedia, Model Identification Using Stochastic Differential Equation Grey-Box Models in Diabetes
Gray-box testing is a combination of white-box testing and black-box testing. A gray-box tester partially knows the internal structure, which includes access to the documentation of internal data structures as well as the algorithms used.
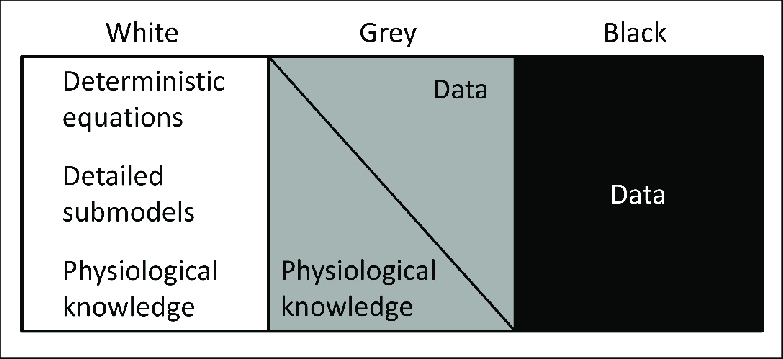
Example: unit test for class
Ref: googletest/googletest/samples
- CMake Setup Update
- Example:
Counterclass - Example:
MyStringclass
CMake Setup Update
# ...
add_executable(
hello_test
hello_test.cpp
)
target_link_libraries(
hello_test
gtest_main
)
add_executable(
sample2_unittest
sample2_unittest.cc
sample2.cc
)
target_link_libraries(
sample2_unittest
gtest_main
)
add_executable(
sample4_unittest
sample4_unittest.cc
sample4.cc
)
target_link_libraries(
sample4_unittest
gtest_main
)
include(GoogleTest)
gtest_discover_tests(hello_test)
gtest_discover_tests(sample2_unittest)
gtest_discover_tests(sample4_unittest)
Example: Counter class
// A sample program demonstrating using Google C++ testing framework.
#ifndef GTEST_SAMPLES_SAMPLE4_H_
#define GTEST_SAMPLES_SAMPLE4_H_
// A simple monotonic counter.
class Counter
{
private:
int counter_;
public:
// Creates a counter that starts at 0.
Counter() : counter_(0) {}
// Returns the current counter value, and increments it.
int Increment();
// Returns the current counter value, and decrements it.
int Decrement();
// Prints the current counter value to STDOUT.
void Print() const;
};
#endif // GTEST_SAMPLES_SAMPLE4_H_
// A sample program demonstrating using Google C++ testing framework.
#include <iostream>
#include "sample4.h"
// Returns the current counter value, and increments it.
int Counter::Increment()
{
return counter_++;
}
// Returns the current counter value, and decrements it.
// counter can not be less than 0, return 0 in this case
int Counter::Decrement()
{
if (counter_ == 0)
{
return counter_;
}
else
{
return counter_--;
}
}
// Prints the current counter value to STDOUT.
void Counter::Print() const
{
std::cout << counter_;
}
#include "sample4.h"
#include "gtest/gtest.h"
namespace
{
// Tests the Increment() method.
TEST(Counter, Increment)
{
Counter c;
// Test that counter 0 returns 0
EXPECT_EQ(0, c.Decrement());
// EXPECT_EQ() evaluates its arguments exactly once, so they
// can have side effects.
EXPECT_EQ(0, c.Increment());
EXPECT_EQ(1, c.Increment());
EXPECT_EQ(2, c.Increment());
EXPECT_EQ(3, c.Decrement());
}
} // namespace
Result:
Running main() from C:\Users\stevenokm\googletest\build\_deps\googletest-src\googletest\src\gtest_main.cc
[==========] Running 1 test from 1 test suite.
[----------] Global test environment set-up.
[----------] 1 test from Counter
[ RUN ] Counter.Increment
[ OK ] Counter.Increment (0 ms)
[----------] 1 test from Counter (2 ms total)
[----------] Global test environment tear-down
[==========] 1 test from 1 test suite ran. (10 ms total)
[ PASSED ] 1 test.
Example: MyString class
// A sample program demonstrating using Google C++ testing framework.
#ifndef GTEST_SAMPLES_SAMPLE2_H_
#define GTEST_SAMPLES_SAMPLE2_H_
#include <string.h>
// A simple string class.
class MyString
{
private:
const char *c_string_;
const MyString &operator=(const MyString &rhs);
public:
// Clones a 0-terminated C string, allocating memory using new.
static const char *CloneCString(const char *a_c_string);
////////////////////////////////////////////////////////////
//
// C'tors
// The default c'tor constructs a NULL string.
MyString() : c_string_(nullptr) {}
// Constructs a MyString by cloning a 0-terminated C string.
explicit MyString(const char *a_c_string) : c_string_(nullptr)
{
Set(a_c_string);
}
// Copy c'tor
MyString(const MyString &string) : c_string_(nullptr)
{
Set(string.c_string_);
}
////////////////////////////////////////////////////////////
//
// D'tor. MyString is intended to be a final class, so the d'tor
// doesn't need to be virtual.
~MyString() { delete[] c_string_; }
// Gets the 0-terminated C string this MyString object represents.
const char *c_string() const { return c_string_; }
size_t Length() const { return c_string_ == nullptr ? 0 : strlen(c_string_); }
// Sets the 0-terminated C string this MyString object represents.
void Set(const char *c_string);
};
#endif // GTEST_SAMPLES_SAMPLE2_H_
// A sample program demonstrating using Google C++ testing framework.
#include "sample2.h"
#include <string.h>
// Clones a 0-terminated C string, allocating memory using new.
const char *MyString::CloneCString(const char *a_c_string)
{
if (a_c_string == nullptr)
return nullptr;
const size_t len = strlen(a_c_string);
char *const clone = new char[len + 1];
memcpy(clone, a_c_string, len + 1);
return clone;
}
// Sets the 0-terminated C string this MyString object
// represents.
void MyString::Set(const char *a_c_string)
{
// Makes sure this works when c_string == c_string_
const char *const temp = MyString::CloneCString(a_c_string);
delete[] c_string_;
c_string_ = temp;
}
#include "sample2.h"
#include "gtest/gtest.h"
namespace
{
// In this example, we test the MyString class (a simple string).
// Tests the default c'tor.
TEST(MyString, DefaultConstructor)
{
const MyString s;
EXPECT_STREQ(nullptr, s.c_string());
EXPECT_EQ(0u, s.Length());
}
const char kHelloString[] = "Hello, world!";
// Tests the c'tor that accepts a C string.
TEST(MyString, ConstructorFromCString)
{
const MyString s(kHelloString);
EXPECT_EQ(0, strcmp(s.c_string(), kHelloString));
EXPECT_EQ(sizeof(kHelloString) / sizeof(kHelloString[0]) - 1,
s.Length());
}
// Tests the copy c'tor.
TEST(MyString, CopyConstructor)
{
const MyString s1(kHelloString);
const MyString s2 = s1;
EXPECT_EQ(0, strcmp(s2.c_string(), kHelloString));
}
// Tests the Set method.
TEST(MyString, Set)
{
MyString s;
s.Set(kHelloString);
EXPECT_EQ(0, strcmp(s.c_string(), kHelloString));
// Set should work when the input pointer is the same as the one
// already in the MyString object.
s.Set(s.c_string());
EXPECT_EQ(0, strcmp(s.c_string(), kHelloString));
// Can we set the MyString to NULL?
s.Set(nullptr);
EXPECT_STREQ(nullptr, s.c_string());
}
} // namespace
Result:
Running main() from C:\Users\stevenokm\googletest\build\_deps\googletest-src\googletest\src\gtest_main.cc
[==========] Running 4 tests from 1 test suite.
[----------] Global test environment set-up.
[----------] 4 tests from MyString
[ RUN ] MyString.DefaultConstructor
[ OK ] MyString.DefaultConstructor (0 ms)
[ RUN ] MyString.ConstructorFromCString
[ OK ] MyString.ConstructorFromCString (0 ms)
[ RUN ] MyString.CopyConstructor
[ OK ] MyString.CopyConstructor (0 ms)
[ RUN ] MyString.Set
[ OK ] MyString.Set (0 ms)
[----------] 4 tests from MyString (11 ms total)
[----------] Global test environment tear-down
[==========] 4 tests from 1 test suite ran. (19 ms total)
[ PASSED ] 4 tests.
Example: Unit Test for Vector & Matrix in Binary File (class ver.) [Source]
Pratices
- Test lab14-1 & lab14-2 with googletest
- Test
Complexclass - Test
Geometry_Comp,Triangle_Comp,Quadrilateral_Comp, andCircle_Comp- Data members
- File input & output
- Test
Example: Unit Test for Vector & Matrix in Binary File (class ver.)
CMakeLists.txt
cmake_minimum_required(VERSION 3.14)
project(lecture18_ex)
# GoogleTest requires at least C++11
set(CMAKE_CXX_STANDARD 11)
include(FetchContent)
FetchContent_Declare(
googletest
URL https://github.com/google/googletest/archive/609281088cfefc76f9d0ce82e1ff6c30cc3591e5.zip
)
# For Windows: Prevent overriding the parent project's compiler/linker settings
set(gtest_force_shared_crt ON CACHE BOOL "" FORCE)
FetchContent_MakeAvailable(googletest)
enable_testing()
add_executable(
lecture18_unittest
lecture18_unittest.cpp
)
target_link_libraries(
lecture18_unittest
gtest_main
)
include(GoogleTest)
gtest_discover_tests(lecture18_unittest)
lecture18_ex.h
#include <iostream>
#include <fstream>
#include <cmath>
#ifndef LECTURE18_EX_H
using namespace std;
class Vector_3D; // forward declaration
class Point_3D // represents a point in 3D space
{
private:
// record the x coordinate
double m_x;
// record the y coordinate
double m_y;
// record the z coordinate
double m_z;
public:
Point_3D(const double &arg_x = 0, const double &arg_y = 0,
const double &arg_z = 0);
Point_3D(const Point_3D &arg_point);
// Destructor
~Point_3D() // destructor
{
// do nothing, because we don't
// have any dynamic memory
}
// modify the x, y and z coordinate
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
void set(const double &arg_x, const double &arg_y, const double &arg_z);
// get the x, y and z coordinate
double get_x() const;
double get_y() const;
double get_z() const;
// calculate the distance between two points
// in form of a vector
Vector_3D operator-(const Point_3D &arg_point) const;
// friend class
friend class Vector_3D;
// print the x and y coordinate in format (x, y, z)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os, const Point_3D &arg_point);
// read the coordinate of a point from the input,
// format: (x, y, z) and ignore space
friend std::istream &operator>>(std::istream &arg_is, Point_3D &arg_point);
};
// Vector_3D class declaration
class Vector_3D
{
private:
// define the three factor of the basis vectors
// on the x, y, z axes
double m_x, m_y, m_z;
public:
// Constructor
Vector_3D(const double &arg_x = 0.0, const double &arg_y = 0.0,
const double &arg_z = 0.0);
Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2);
// Copy constructor
Vector_3D(const Vector_3D &arg_vector);
// Destructor
~Vector_3D()
{
// do nothing
}
// set the three factor of the basis vectors
void set_vector(const double &arg_x, const double &arg_y,
const double &arg_z);
void set_vector(const Point_3D &arg_point1, const Point_3D &arg_point2);
void set_x(const double &arg_x);
void set_y(const double &arg_y);
void set_z(const double &arg_z);
// get the three factor of the basis vectors
double get_x() const;
double get_y() const;
double get_z() const;
// assign operator
Vector_3D &operator=(const Vector_3D &arg_vector);
// calculate the length of the Vector_3D
double length();
// calculate the dot product of two vectors
int dot(const Vector_3D &);
// calculate the cross product of two vectors
Vector_3D cross(const Vector_3D &);
// write the Vector_3D in binary format
void write_binary(std::ofstream &arg_ofs);
// read the Vector_3D in binary format
void read_binary(std::ifstream &arg_ifs);
// print the Vector_3D in format (x, y, z)
// accessable to const object
friend std::ostream &operator<<(std::ostream &arg_os,
const Vector_3D &arg_point);
// read the factors of a vector from the input,
// format: (x, y, z) and ignore space
friend std::istream &operator>>(std::istream &arg_is,
Vector_3D &arg_point);
};
// Point_3D class implementation
// Constructor & Default constructor
// initialize data members, with default values
Point_3D::Point_3D(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x),
m_y(arg_y),
m_z(arg_z)
{
}
// Copy constructor
// copy the data members from the given object
Point_3D::Point_3D(const Point_3D &arg_point)
: m_x(arg_point.m_x),
m_y(arg_point.m_y),
m_z(arg_point.m_z)
{
}
// modify the x and y coordinate
// we use `arg_` to indicate the arguments
// and re-write with setter
void Point_3D::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Point_3D::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Point_3D::set(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
// get the x coordinate and y coordinate
// accessable to const object
double Point_3D::get_x() const
{
return m_x;
}
double Point_3D::get_y() const
{
return m_y;
}
double Point_3D::get_z() const
{
return m_z;
}
// calculate the distance between two points
// in form of a vector
Vector_3D Point_3D::operator-(const Point_3D &arg_point) const
{
return Vector_3D(*this, arg_point);
}
// print the point in the format (x, y, z)
std::ostream &operator<<(std::ostream &arg_os, const Point_3D &arg_point)
{
arg_os << "(" << arg_point.m_x << ", " << arg_point.m_y
<< ", " << arg_point.m_z << ")";
return arg_os;
}
// read the coordinate of a point from the input,
// format: (x, y, z) and ignore space
std::istream &operator>>(std::istream &arg_is, Point_3D &arg_point)
{
string str_x, str_y, str_z, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ','))
{
if (getline(arg_is, str_z, ')'))
{
arg_point.m_x = stod(str_x);
arg_point.m_y = stod(str_y);
arg_point.m_z = stod(str_z);
}
}
}
}
return arg_is;
}
// Vector_3D class implementation
// Constructor
Vector_3D::Vector_3D(const double &arg_x, const double &arg_y,
const double &arg_z)
: m_x(arg_x), m_y(arg_y), m_z(arg_z)
{
}
Vector_3D::Vector_3D(const Point_3D &arg_point1, const Point_3D &arg_point2)
: m_x(arg_point2.m_x - arg_point1.m_x),
m_y(arg_point2.m_y - arg_point1.m_y),
m_z(arg_point2.m_z - arg_point1.m_z)
{
}
// Copy constructor
Vector_3D::Vector_3D(const Vector_3D &arg_vector)
: m_x(arg_vector.m_x), m_y(arg_vector.m_y), m_z(arg_vector.m_z)
{
}
// set the three factor of the basis vectors
void Vector_3D::set_vector(const double &arg_x, const double &arg_y,
const double &arg_z)
{
m_x = arg_x;
m_y = arg_y;
m_z = arg_z;
}
void Vector_3D::set_vector(const Point_3D &arg_point1,
const Point_3D &arg_point2)
{
m_x = arg_point2.m_x - arg_point1.m_x;
m_y = arg_point2.m_y - arg_point1.m_y;
m_z = arg_point2.m_z - arg_point1.m_z;
}
void Vector_3D::set_x(const double &arg_x)
{
m_x = arg_x;
}
void Vector_3D::set_y(const double &arg_y)
{
m_y = arg_y;
}
void Vector_3D::set_z(const double &arg_z)
{
m_z = arg_z;
}
// get the three factor of the basis vectors
double Vector_3D::get_x() const
{
return m_x;
}
double Vector_3D::get_y() const
{
return m_y;
}
double Vector_3D::get_z() const
{
return m_z;
}
// assign operator
Vector_3D &Vector_3D::operator=(const Vector_3D &arg_vector)
{
m_x = arg_vector.m_x;
m_y = arg_vector.m_y;
m_z = arg_vector.m_z;
return *this;
}
// calculate the length of the Vector_3D
double Vector_3D::length()
{
// calculate the length of the Vector_3D
return sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
}
// calculate the dot product of two vectors
int Vector_3D::dot(const Vector_3D &arg_v)
{
// calculate the dot product of two vectors
return m_x * arg_v.m_x + m_y * arg_v.m_y + m_z * arg_v.m_z;
}
// calculate the cross product of two vectors
Vector_3D Vector_3D::cross(const Vector_3D &arg_v)
{
// calculate the cross product of two vectors
Vector_3D v;
v.m_x = m_y * arg_v.m_z - m_z * arg_v.m_y;
v.m_y = m_z * arg_v.m_x - m_x * arg_v.m_z;
v.m_z = m_x * arg_v.m_y - m_y * arg_v.m_x;
return v;
}
// write the vector to the file in binary format
void Vector_3D::write_binary(std::ofstream &arg_ofs)
{
arg_ofs.write((char *)&m_x, sizeof(double));
arg_ofs.write((char *)&m_y, sizeof(double));
arg_ofs.write((char *)&m_z, sizeof(double));
}
// read the vector from the file in binary format
void Vector_3D::read_binary(std::ifstream &arg_ifs)
{
arg_ifs.read((char *)&m_x, sizeof(double));
arg_ifs.read((char *)&m_y, sizeof(double));
arg_ifs.read((char *)&m_z, sizeof(double));
}
// print the point in the format (x, y, z)
std::ostream &operator<<(std::ostream &arg_os, const Vector_3D &arg_vector)
{
arg_os << "(" << arg_vector.m_x << ", " << arg_vector.m_y
<< ", " << arg_vector.m_z << ")";
return arg_os;
}
// read the factors of a vector from the input,
// format: (x, y, z) and ignore space
std::istream &operator>>(std::istream &arg_is, Vector_3D &arg_vector)
{
string str_x, str_y, str_z, temp;
if (getline(arg_is, temp, '(')) // ignore the first '('
{
if (getline(arg_is, str_x, ','))
{
if (getline(arg_is, str_y, ','))
{
if (getline(arg_is, str_z, ')'))
{
arg_vector.m_x = stod(str_x);
arg_vector.m_y = stod(str_y);
arg_vector.m_z = stod(str_z);
}
}
}
}
return arg_is;
}
#endif // LECTURE18_EX_H
lecture18_ex.cpp
#include <iostream>
#include <fstream>
#include <cmath>
#include "lecture18_ex.h"
using namespace std;
// main function
int main()
{
Vector_3D v1(1, 2, 3);
Vector_3D v2(4, 5, 6);
cout << "v1 = " << v1 << endl;
cout << "v2 = " << v2 << endl;
// save the vector to the file in binary format
ofstream ofs("vector.bin", ios::binary | ios::trunc);
v1.write_binary(ofs);
v2.write_binary(ofs);
ofs.close();
// read the vector from the file in binary format
ifstream ifs("vector.bin", ios::binary);
Vector_3D v3, v4;
v3.read_binary(ifs);
v4.read_binary(ifs);
cout << "v3 = " << v3 << endl;
cout << "v4 = " << v4 << endl;
// or read/write whole object
ofstream ofs2("vector_whole.bin", ios::binary | ios::trunc);
ofs2.write((char *)&v1, sizeof(Vector_3D));
ofs2.write((char *)&v2, sizeof(Vector_3D));
ofs2.close();
ifstream ifs2("vector_whole.bin", ios::binary);
Vector_3D v5, v6;
ifs2.read((char *)&v5, sizeof(Vector_3D));
ifs2.read((char *)&v6, sizeof(Vector_3D));
cout << "v5 = " << v5 << endl;
cout << "v6 = " << v6 << endl;
// NOTE: compaire "vector.bin" and "vector_whole.bin"
return 0;
}
lecture18_unittest.cpp
#include "lecture18_ex.h"
#include "gtest/gtest.h"
namespace
{
TEST(Vector_3D, Init)
{
Vector_3D v1(1, 2, 3);
EXPECT_EQ(1, v1.get_x());
EXPECT_EQ(2, v1.get_y());
EXPECT_EQ(3, v1.get_z());
}
TEST(Vector_3D, WriteFile)
{
Vector_3D v1(1, 2, 3);
Vector_3D v2(4, 5, 6);
ofstream ofs("vector_writetest.bin", ios::binary | ios::trunc);
v1.write_binary(ofs);
v2.write_binary(ofs);
ofs.close();
ifstream ifs("vector_writetest.bin", ios::binary);
// test v1
double x, y, z;
ifs.read((char *)&x, sizeof(double));
ifs.read((char *)&y, sizeof(double));
ifs.read((char *)&z, sizeof(double));
EXPECT_EQ(x, v1.get_x());
EXPECT_EQ(y, v1.get_y());
EXPECT_EQ(z, v1.get_z());
// test v2
ifs.read((char *)&x, sizeof(double));
ifs.read((char *)&y, sizeof(double));
ifs.read((char *)&z, sizeof(double));
EXPECT_EQ(x, v2.get_x());
EXPECT_EQ(y, v2.get_y());
EXPECT_EQ(z, v2.get_z());
ifs.close();
}
TEST(Vector_3D, ReadFile)
{
Vector_3D v1(1, 2, 3);
Vector_3D v2(4, 5, 6);
ofstream ofs("vector_readtest.bin", ios::binary | ios::trunc);
v1.write_binary(ofs);
v2.write_binary(ofs);
ofs.close();
ifstream ifs("vector_readtest.bin", ios::binary);
// test v1
Vector_3D v3;
v3.read_binary(ifs);
EXPECT_EQ(v1.get_x(), v3.get_x());
EXPECT_EQ(v1.get_y(), v3.get_y());
EXPECT_EQ(v1.get_z(), v3.get_z());
// test v2
v3.read_binary(ifs);
EXPECT_EQ(v2.get_x(), v3.get_x());
EXPECT_EQ(v2.get_y(), v3.get_y());
EXPECT_EQ(v2.get_z(), v3.get_z());
ifs.close();
}
} // namespace
Result
Running main() from C:\Users\stevenokm\googletest\build\_deps\googletest-src\googletest\src\gtest_main.cc
[==========] Running 3 tests from 1 test suite.
[----------] Global test environment set-up.
[----------] 3 tests from Vector_3D
[ RUN ] Vector_3D.Init
[ OK ] Vector_3D.Init (0 ms)
[ RUN ] Vector_3D.WriteFile
[ OK ] Vector_3D.WriteFile (6 ms)
[ RUN ] Vector_3D.ReadFile
[ OK ] Vector_3D.ReadFile (1 ms)
[----------] 3 tests from Vector_3D (15 ms total)
[----------] Global test environment tear-down
[==========] 3 tests from 1 test suite ran. (22 ms total)
[ PASSED ] 3 tests.
