Lecture 12: Function & Reference (3)
Function call stack
Function 會有呼叫的 stack,讓我們可以知道哪些 function 被呼叫了,以及呼叫的順序。
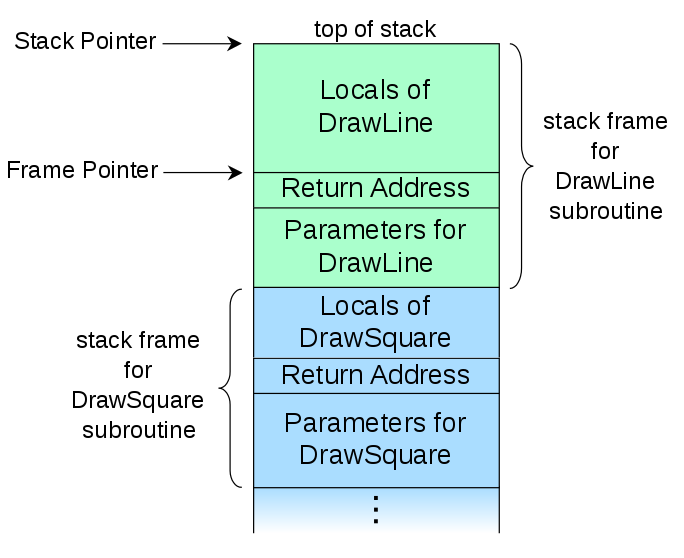
Call Stack 的狀況:
- 從下而上,每個 function 呼叫都會加入一個 call stack,並且把自己的名稱加入。
- 越上方的 function 呼叫越新被呼叫,越下方的 function 呼叫越舊被呼叫。
- 每次執行的時候,皆是執行最上方的 function。
- 可透過 return address 找到呼叫的 function,並將結果回傳給呼叫的 function。
Function Caller & Callee
Example:
#include <iostream>
void print_operand(int operand) // callee
{
std::cout << "Operand: " << operand << std::endl;
}
void print_result(int result) // callee
{
std::cout << "Result: " << result << std::endl;
}
int add(int a, int b) // callee & caller
{
print_operand(a);
print_operand(b);
int c = a + b;
print_result(c);
return c;
}
int main(int argc, char *argv[]) // caller
{
int a = 1;
int b = 2;
int c = add(a, b);
return 0;
}
Recursion
Recursion 是一種遞迴的程式碼,可以讓我們 function 自己呼叫 function 自己。
Example: Fibonacci sequence
#include <iostream>
int fibonacci(int n) // caller & callee
{
if (n == 0)
{
return 0;
}
else if (n == 1)
{
return 1;
}
else
{
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
int main(int argc, char *argv[]) // caller
{
int n = 10;
std::cout << "Fibonacci sequence of " << n << ": ";
for (int i = 0; i < n; i++)
{
std::cout << fibonacci(i) << " ";
}
std::cout << std::endl;
return 0;
}
Expanded version: i = 3
#include <iostream>
int fibonacci_0(void)
{
return 0;
}
int fibonacci_1(void)
{
return 1;
}
int fibonacci_2(void)
{
return fibonacci_0() + fibonacci_1();
}
int fibonacci_3(void)
{
return fibonacci_1() + fibonacci_2();
}
int main(int argc, char *argv[]) // caller
{
int n = 3;
std::cout << "Fibonacci sequence of " << n << ": ";
std::cout << fibonacci_1() << " ";
std::cout << fibonacci_2() << " ";
std::cout << fibonacci_3() << " ";
std::cout << std::endl;
return 0;
}
Infix notation & Calculation
一般的數學式皆是 infix notation,也就是從左到右的計算,並且運算子是在兩運算元的中間。
Example: \(1 + 2 * 3 = 9\) (沒有先乘後加的 infix notation)
進行運算的時候,會先運算左手邊運算子,再運算右手邊運算子。如: $$1 + 2 * 3 = (1 + 2) * 3 = (3) * 3 = 9$$
我們可以由左至右依序運算就可以得到答案,但也可以從右到左,使用遞迴的方式來運算。
Method:
expression = expression op expression | number
number = [0-9]+
op = '+' | '-' | '*' | '/'
Example:
$$ \begin{align} 1 + 2 * 3 &= (1 + 2) * 3 \\ &= ((1) + 2) * 3 \\ &= (1 + 2) * 3 \\ &= (3) * 3 \\ &= 3 * 3 \\ &= 9 \end{align}$$
Postfix notation
另一種數學運算式表達法式 postfix notation,也是從左到右的計算,但運算子是在兩運算元或運算式的右邊。
Example: 1 2 + 3 * = 9
進行運算的時候,從左至右依序讀取,碰到運算子時會將最近讀取或是運算結束的運算元拿來進行運算,並將運算結果儲存回去。如:
1 2 + 3 * = (1) 2 + 3 *
= (1 2) + 3 *
= (1 2 +) 3 *
= (3) 3 *
= (3 3) *
= (3 3 *)
= (9)
當然這也可以從右到左,使用遞迴的方式來運算,但是會有尋找運算子的兩運算元的問題。
Find postfix operands using recursion
因為 postfix notation 是從右到左的使用該運算子的兩運算元,所以我們可以用遞迴的方式來找到運算元。
Method:
- postfix 運算
- 使用傳入的最後一個 token 的位置,並記錄下來。
- 跳過 1. 記錄的最後一個運算子,從右往左尋找
- 如果是運算元,則回傳目前的運算元作為運算結果。
- 如果是運算子,則從目前位置開始視為新的 postfix notation,重複步驟 1 到 2,並紀錄回傳的結果為運算元 1。
- 透過更新的上次運算最後位置,從該位置繼續視為新的 postfix notation,重複步驟 1 到 2,並紀錄回傳的結果為運算元 2。
- 更新最後位置為運算元 2 的最後位置。
- 回傳運算元 1 & 2 的運算結果。
Example:
1 2 3 4 + + * = 1 2 3 4 + + (*)
= (1 2 3 4 + +) *) // find operand1
= (1 2 3 4 + (+)) *) // find operand1
= ((1 2 3 4 +) +)) *) // find operand1, find operand1
= ((1 2 3 4 (+)) +)) *) // find operand1, find operand1
= ((1 2 3) (4 +)) +)) *) // find operand1, find operand1, found operand1
= ((1 2 (3) (4 +)) +)) *) // find operand1, find operand1, found operand2
= ((1 2) (7 +)) *) // find operand1, find operand1, result
= ((1 (2) (7 +)) *) // find operand1, find operand2
= ((1) (9 *) // find operand1, result
= ((1) (9 *) // find operand2
= 9 // result
Further Reading: Recursion and ProblemSolving
// This algorithm modifies its argument in the process of evaluating it.
float evaluate_prefix(string &prefix_str)
{
char ch = prefix_str[first]; // get character at position first
// Delete first character from prefix_str;
prefix_str = prefix_str.substr(first + 1);
if (is_identifier(ch))
{
return value of the identifier;
}
// if the character is an operator, then
else if (is_operator(ch))
{
op = ch;
operand1 = evaluate_prefix(prefix_str);
operand2 = evaluate_prefix(prefix_str);
return operand1 op operand2;
}
}